chapter 5. System theory
TIME AS VARIABILITY OF NATURAL SYSTEMS:
WAYS OF QUANTITATIVE DESCRIPTION OF CHANGES AND
CREATION OF CHANGES BY SUBSTANTIAL FLOWS
A.P.Levich
1. Time-metabol
©The task of the present study is to discuss one of the possible versions of the construction of time. More specifically, it is to prepare in a consistent way prerequisites for constructing a dynamic theory of natural systems by suggesting an elementary object of the theory, the ways of object variability, the clocks, the space of states, the ways of obtaining variability laws and, as far as possible, interpretation procedures. Another task of the study is to test the construction in an attempt to solve some of the problems of time.
The suggested material does not form a complete study. One should treat it rather as an attempt to create a research programme for studying time.
1.1. The substitutional construction of time
Systems and variability. Natural systems are formed from their elements in a way which cannot be called arbitrary.
The hierarchy principle: Natural systems are hierarchic: any object turns out to be an element of a higher rank object, and any element turns out to be an object consisting of pre-elements.
Thus a living cell consists of molecules, organisms are formed from cells; the latter in turn unite to form populations; populations form communities which in turn can be considered as elements of the biosphere. That is a fragment of the biological hierarchy.
A version of the geological hierarchy: molecules, minerals, rocks, sediments, terrains.
The geographic hierarchy: molecules, sediments, faces, landscapes, physical-geographic districts, provinces, zones, countries, continents, the dry land, the geographic shell (according to I.A.Solntsev, from the book by I.I.Mikhailov (1985)).
A sketch of the astronomical hierarchy: molecules, bodies, planet systems, star associations, galaxies... (All these examples are not rigorous constructions, rather, these are just illustrations to enlighten the general considerations.)
The hierarchy structure of systems is not only a natural-scientific generalization but also one of the axiomatization methods within sets theory, making it possible to avoid logical contradictions which can appear from uncontrolled construction of objects from elements. Thus, if each element is ascribed to a certain type, then sets (natural objects) are formed from elements of the same type (Whitehead and Russel 1910; Frenkel and Bar-Hillel 1958). The types of objects are usually marked by natural numbers. It is significant that in the suggested axiomatics all the concepts acquire the character of types: in a rigorous presentation (Levich 1982) a specification of any construction (an object, an element, belonging, unification or intersection, time, space, etc.) must be followed by specification of a type. Only in an unformalized presentation, when the construction type is quite clear from the context, its identification is frequently omitted.

When hierarchic systems are considered, the question commonly occurs on how far "up" and "down" the hierarchy levels are extended. It appears convenient for the author to hold on to the following position: the depth of a hierarchy is determined by the existence of operational ways to identify the elements of the "remote" levels. For any identification technology there exists a level of unidentified elements, the one to be taken for a boundary of a hierarchy (a relative one, since the available object studying methods can change).
It is convenient to call the number of structure levels, which are taken into consideration, the depth of a system. The hierarchy principle requires that the elementary object of the theory, "a system", should be of necessity a hierarchic construction (Fig.1).
The words "the set of elements of a system varies" will mean that either new elements appear (growth of a system), or that some of the elements are replaced by other copies of these (a stationary state of a system), or that some of the elements are lost (system degradation and destruction).
The variability principle: In all the natural systems there always exists the phenomenon of varying the constituent element set. Any variation of a system consists in variation of the set of elements at a level of certain depth in the hierarchy containing the system.
I will call the system element variation phenomenon the general process of natural systems.
I would like to mention the general processes for objects belonging to the canonical example of biological hierarchy.
The general process in living cells is metabolism, the process of replacing molecules forming the cell. For multicellular organisms the general process is growth, during which new cells appear and the existing ones are replaced or disappear. The number dynamics, summing up the births and deaths of individuals, is the general process for a population. Species replacement, called succession, is a manifestation of the general process in ecological communities. The change of associations of species in the Earth's biosphere is called the evolution process.
The hierarchy and variability principles make it possible to unify the variety of variability manifestations (quality, relation, connection changes, etc.): only the system element numbers are varied, or certain elements are replaced by others. Qualitative peculiarities of the variations are described in terms of different levels of system structure at which the elements are changed. Thus to describe the variability means to find the hierarchy levels at which the sets of pre-elements are changed.
It should be noted that the term "variability" is often used in some context other than dynamical. One can speak of spatial (for instance, geographical) variability of biological or social objects. The term "variability" is also used to describe the diversity of objects in taxons of certain classifications (atoms in the chemical element system, butterflies in a collection). Choosing the position of historical method, one may try to reduce all the variability types to their appearance resulting from only dynamical evolutionary variability; however, in the framework of the present paper it is offered to discuss only manifestations of "pure" dynamic variability of natural objects.
Along with the terms "element set variation" and "the general process", let us use their synonym "the course of time". Thus the postulate of existence of a "pre-time" is replaced by the postulate of the existence of the general process. Such a modification, without making clear the "nature" of time, is nevertheless useful since it defines the events operationally in terms of system element replacing.
Measurement of time. The general process, unifying the variability, thus introduces the pre-time of natural systems. To introduce a parametric time, i.e., a representation of the variability process by numbers, it is necessary to make a methodological digression.
"In the descriptions of the measurement process, so essentially simple, one can notice a significant reticence in many courses of mechanics and physics which have become classic. It was my task to establish more determinacy in the problem and, along with that, to show what a great arbitrariness is present in establishing a measurement" (Friedmann 1965, p.16).
Namely, if a relation of order is established on a set
K of the properties of a certain fragment of the reality, then those properties are called intensities. If the relation of "equal spacing" is defined for the intensities K1, K2 and K3, i.e., K1 is smaller than K2 as much as K2 is smaller than K3, then these intensities are called measurable. For example, the volumes of geometric bodies are measurable intensities, while the quality of students' knowledge is an unmeasurable one.The mapping
A: K ® R of a class of properties K into a numerical set R is called arithmetization of the properties K. A monotonic arithmetization of intensities is called an estimate. Examples: estimation of students' knowledge using five- or hundred-grade scales; juxtaposition of the corresponding electromagnetic wavelengths to the colours of the solar light spectrum. Estimations of measurable intensities, satisfying the condition A(K2) - A(K1) = A(K3) - A(K2), are called measurements. Any two arithmetizations, if they are measurements, can different from each other only linearly, i.e., only zero points or measurement units can be different.Thus "any class of properties can be arithmetized; if these properties are made intensities (by our definition), then we can... estimate them by numbers; finally, if the intensities are made (again by our definition) measurable intensities, then we can... measure them; a measurement will contain certain arbitrariness, removed by establishing the zero point and the measurement unit" (Friedmann 1965, p.15).
Thus to make it possible to measure the variability it is necessary to have an agreement (an instruction, an imperative...) of which intensity differences are taken as equal.
The imperativity principle: A standard object belonging to a certain level of system structure, is called a clock. Changes of the set of elements of the standard object by one element are considered to be equal and can be taken as the unit of time.
The necessity of such an agreement is realized by natural scientists (Milne 1948): A priori we can take any dynamic phenomenon and use its development to define the time scale. However, a uniform natural scale does not exist, since we cannot say what is meant by the word "uniform" with respect to time; we cannot catch the present minute and put it side by side with the next one. It is sometimes said that a uniform time scale is defined by periodic phenomena. However, allow me to ask a question: can anybody tell us that the two periods, following one another, are equal?
In physics the role of a uniformity agreement is played by Newton's first law: the time intervals during which a body, moving without interaction with other bodies, covers equal distances, are called equal (Thompson and Tait 1890).
Let us introduce a few definitions to illustrate the ways of conceptual basis construction becoming evident after the imperativity principle is adopted.
A type i event x (a synonym: a time instant) for an object A of the type i + 1 is a replacement of the element x in the object A. We will also call an event the replaced element x itself.
A substitutional clock is a natural object whose element substitution is taken as a uniform variability standard.
The proper time (Vasilyev et al. 1974) or the proper age (Zotin and Alexeyeva 1984) of an organism can be defined from the counts of consumed oxygen molecules.
The proper age of an organism can be measured by the number of newly formed cells; by wound healing area (Noüy 1936); by growth of specified organs of the body, e.g., the size of eye crystalline lens is considered to be one of the best biological age markers for mammals (Shaher 1982); the number of separated cells of yeast, being their only stable age characteristic, unlike any chronological dating (Voitenko 1985).
The scale of age stages of a plant (Cheburayeva 1977): germination, juvenile, immature, young vegetative, young, mature, old, subsenile, senile stages) is treated as a specific form of ontogenetic time accounting, such that the intervals between the neighbouring age stages are taken to be equal (Uranov 1975). The same is the case for the scale using the instants of pea alternate leafs appearance (Thornwaite 1953).
The dynamics of microalgae populations is well described in terms of consumed biogenic elements which are limiting factors of community development (Levich 1980; Levich et al. 1986). The maturity parameter of an ecological community (a concept close to ecological age) is introduced by M.E.Vinogradov and E.A.Shushkina (1983): the maturity index is connected with the ratio of community destruction (commonly measured by the amount of biogenic chemical elements leaving the community) with respect to primary production (proportional to the amount of biogenic elements entering the community).
In paleontology the analysis of large groups of organisms on the basis of measuring the number of taxons is quite common. One usually takes into account those characteristics which refer to a single stratigraphic division, namely, the overall number of taxons and the numbers of those appeared and died out (Dmitriev 1978).
A proper time interval of depth k between an event a of type k and another event b of type k for an arbitrary system of type i is, by definition, the number of type k elements which have been replaced in the system as a result of the general process. Thus the proper time of depth k for a type i system is measured by the clocks of the type i - k + 1 obtained by unification of type i - k + 1 elements belonging to the above system.
If the concept of event simultaneity can be correctly introduced, then there is a possibility to measure not only the proper time of a system but also its time by an arbitrary clock.
External time (time by the clock C). A time interval between the events a and b by the clock C is the proper time interval of the object C between the event x belonging to C and simultaneous with a and the event y belonging to C and simultaneous with b.
The age T of an object A according to some clock is the time elapsed by this clock between the events which have occurred in the object A and consisted in the appearance of an element d in A and its leaving A (d belongs to A).
The amount of oxygen consumed by an animal from its "first sigh" and "last breath" can serve as its physiological age. If the Rubner rule is valid (Zotin and Alexeyeva 1984), then this quantity is the same for all representatives of a single biological species. Moreover, if one assumes that the oxygen consumption rate for oxidation of a unit mass of food is constant, then the physiological age corresponds to the amount of consumed food, i.e., one speaks of a certain substrate-energetic proper time scale of an organism. The Rubner rule is confirmed by experimental results obtained mostly on rodents, insects and unicellulars: food limitation leads to life prolongation (McCay 1935; Bauer 1935).
The present of an object. Given an object A of type i + k and its type i element d, I will call "the present of the level k for the object d with respect to the superobject A" the time interval (by some clock) between the events consisting of d entering A and d leaving A. The quantity T may be called "thickness of the present". I would like to note that the thickness of the present for an object d with respect to the superobject A is equal to the age of A measured by the element d.
It is natural to call the events which took place before the object d entered the object A "the past with respect to the superobject A". Accordingly one can define "the future of the object d with respect to the superobject A". It is evident that the past, present and future of an object are relative since they depend entirely on the choice of the superobject A (that is, the higher level of the natural hierarchy and the representative A of that level which contains the object d).
The multicomponent nature of the substitutional time has turned out to be essential for the introduction of the past, present and future. The multicomponent nature makes it possible to separate operationally the non-coinciding properties of time: the temporal sequence "past - present - future" for an object d is defined only with respect to its superobjects while the sequence "earlier - later" is determined by a clock of the same type as the subobjects of the object d.
I would like to note that the ideas connected with the "thickness of the present" have been induced by the works of G.E.Mikhailovsky which are also presented in this book.
Substitutional time and a substitutional object of the theory. In Latin the word "substitucio" means replacement. The clock construction operating with element replacements in systems, is called substitutional according to the tradition to use Latin terms in scientific texts. In the following we will also use a synonym of the word "substitutional", namely, the word "metabolic" of ancient Greek origin.
The scientific tradition traced back to Heraclites and Aristoteles, which connects time with the perception and experiencing changes in the World. Aristoteles (1981, Comment 9 of Chapter 11 of Book 4) distinguished changes as movement in a broad sense (metabol©), as emergence and destruction (genesis kai phthora), as qualitative transformations (alloisis) and as mechanical motion (kinesis).
The above variability axiomatics: the general process = generalized movement = the course of time - does not refer to a separate type of transformations and apparently corresponds to the term "metabol©". By S.V.Meyen's proposal, the described construction of time is called the metabolic time of natural systems (see also the term used in papers by Goodwin (1966), G.E.Mikhailovsky (1982) and Schmidt-Nielson (1987)). However, the word "metabolic" is to be understood in a much wider sense than just biochemical metabolism of living cells and organisms.Usually one imagines time as some cyclic process, or the one connected with repeated periods: alternation of day and night, oscillations of a pendulum and ticking of a clock, metronome rythme, ... Measurement of time in physics is always connected with periodic processes: rotation of the Earth, mechanical or electromagnetic oscillations. The suggested construction replaces "cyclic" clocks by "substitutional" ones, transferring the accent to processes, which are not necessarily periodic but can be nonstationary and evolutionary. However, the "cyclic" and "substitutional" process representation can be complementary to each other.
In quantum-mechanical field description there exists a deep correspondence between the representations of phenomena in the language of frequencies and that of particle replacements ("creation" and "annihilation"). It is involved in the second quantization method.
Metabolic time is a property of a system which is of necessity open with respect to elements of a certain structure level.
The substitutional construction of time creates an archetype of hierarchic and metabolic view of the World, or, more precisely, of natural systems: the elementary object of the theory does not resemble "points" or "states", it is a hierarchic object and necessarily an open one.
To describe a metabolic object rigorously, new mathematical means are required. The hierarchic nature of an object can be described in terms of the armade construction (Levich 1982), which explicitly introduces into mathematics, apart from a tangle of the traditional algebraic, topological and order structures (Bourbaki 1963), a hierarchic algebraic structure (on the basis of the already mentioned theory of types). However, the sets- theoretic foundations of mathematics are apparently insufficient for a formal description of a metabolic object: one needs a formalism for describing systems with appearing and disappearing elements (this circumstance was noticed by A.A.Sharov). Maybe that could be achieved if a softer form of extensionality were adopted but possibly more radical means are required to operate with "dynamic sets" instead of those with elements determined once and forever. A good implicit example of a "dynamic set" is a "metapopulation" of organisms, including, along with the individuals existing at the moment, their ancestors and potential descendants.
One more feature of a formal description of a substitutional object is the necessity of rejecting Archimedes' axiom: no "mechanical addition" of pre-level elements can result in a consistent object of a given level. Thus the algebraic properties of the objects (universums) from different levels imply that those universums are related to each other as objects of nonstandard analysis (Robinson 1966).
1.2. Properties of substitutional time
The multicomponent character. Proper times of different depths belonging to a system form a multicomponent quantity for which I would like to suggest the name "the pyramid of time" of a given system (Fig.1). The term "pyramid" looks rather awkward but the other term coming to mind, "the vector of time", would be mathematically inaccurate, since neither a coordinate frame is introduced, nor transformations under which the studied multicomponent quantity would behave as a vector.
The proper time
t1 of depth 1 for a cell is measured by the number of molecules replaced in that cell. In a similar manner the time of an organism is measured by the number of replaced cells (Noüy 1936; Shaher 1982). The time t1 for a population is measured by the birth-death balance for the members of the population (Abakumov 1969; Alexeyev 1975; Svirezhev and Pasekov 1982). For a community t1 is the number of species changed in the succession. The biospheric time t1 is counted by associations of living organisms, replacing each other, disappearing and forming again.An ecological community can be imagined as a unity of individuals belonging to all the species forming the community; the balance of changes of the total number of individuals determines the value of the time
t2 of depth 2 for the community. For an organism t2 is determined by the molecular flow through the organism (Vasilyev et al. 1974). The biospheric t2 is the number of replaced species (Dmitriev 1978).To find solutions of many ecological problems it is convenient to represent a community as a pool of a certain biogenic chemical element limiting the development of organisms (e.g., carbon, nitrogen or phosphorus). The sum of molecular number changes in the pool (in practice such quantities are estimated in terms of mass or concentration units) is the proper time of depth
3 for the community (e.g., for algocoenoses - Levich et al. 1986a) or 4 (for communities of multicellular organisms - Vinogradov and Shushkina 1983).Usually one of the components is chosen for measuring time, nearly always the deepest one, close to the indistinguishability level and connected with physical processes (e.g., the electromagnetic scale corresponding to photon "replacements" in atoms). The imperativity principle allows one to choose a system belonging to any level of natural hierarchy as a reference clock.
The ideas that time is more than one-dimensional repeatedly emerged in natural science. "For life viewed from the geochemical standpoint, time is expressed in three different processes: firstly, the time of individual existence, secondly, the generation changing time, with the form of life unchanged, and, thirdly, the evolutionary time, i.e., that of changing forms along with generations" (Vernadsky 1988, p.231). "The existence of many time scales is without doubt the most significant aspect of life.... For instance, there exist the physical time (in equations of motion), the catalytic time (necessary for describing fermentative reactions), the time of cellular fission, the ecological succession time and, finally, the evolutionary time..." (from G.Patti's letter addressed to C.H.Waddington. On the way..., 1970, pp.177-178). G.E.Mikhailovsky (1982) introduces the complex time of living organisms (see also G.E.Mikhailovsky's chapter in this book). Its real part is the ontogenetic time of an organism while the imaginary one is determined by the stage of the self-reproduction processes. N.I.Moiseyeva (1980) insists that a three-dimensional biological time should be introduced.
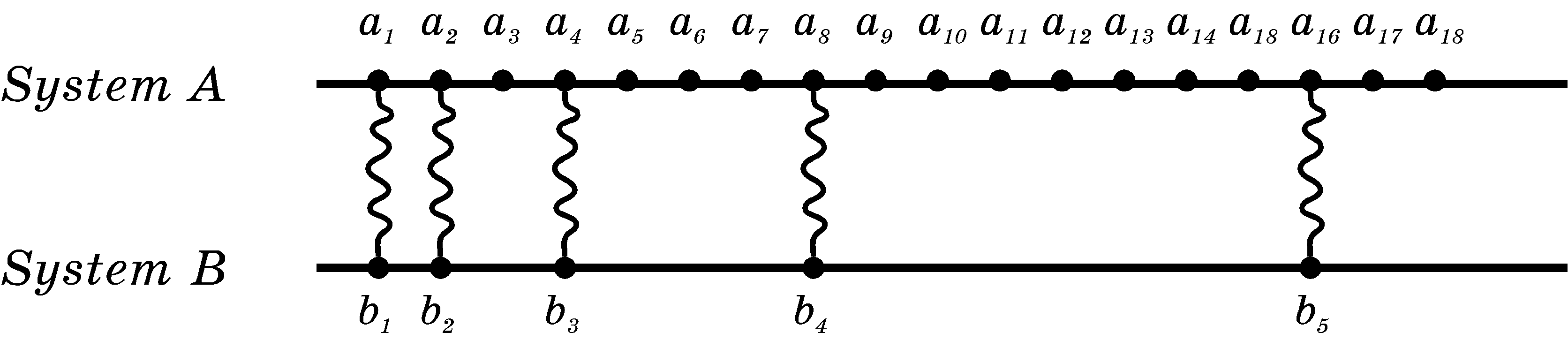
Non-uniformity of the course. The freedom of choosing reference objects for time measurements allows one to ask the question, whether or not all the processes are commensurable, i.e., can any of the existing processes serve as a reference for any other process? We are forced to answer negatively, since due to the imperativity principle the time intervals, equal as measured by one clock, can turn out to be different as measured by another clock (a schematic example in Fig.2 illustrates the mutual non-uniformity of two time scales).
The non-uniformity of metabolic time, as a consequence of the hierarchy and imperativity principles, is discovered only when several time scales are present. If a scale is unique, the course of time is uniform by the definition contained in the imperativity principle. For example: "The absolute, true, mathematical time as it is, by its very nature, without any relation to anything outside, flows uniformly and is also called duration. All the motions can accelerate or decelerate, while the flow of absolute time cannot change" (Newton 1687, translated from Russian ed.).
A choice of a "sufficiently deep" component of the pyramid of time as a unique representative of the whole pyramid leads to adoption of a uniformity standard for physical time scales. The man-made instruments for measuring time, such as a burning candle with marks drawn along it, sand, water, pendulum, astronomical, atomic and pulsar clocks, are most equally mutually uniform.
Note that the physical processes aspiring to be used as time standards (the rotating Earth, the ephemeris time, the "second world time" taking into account the seasonal corrections to the rotation of the Earth, the tropic year, radiation of caesium atoms) represent the clocks of significantly different uniformities from the standpoint of the modern level of accuracy (Martynov 1961).
The choice of a clock is to a large extent a psychological problem: although very different natural processes can be suggested to play the role of standard clocks, the ones convenient for a man are preferred. I.e., those in agreement with the course of "time of the consciousness", which in turn is induced by the planetary conditions of human life. "As a matter of fact, the uniform motion concept already assumes the existence of time, while the expression "the stars are moving uniformly" means only that we call the stellar motion uniform. The uniformity of motion is an entirely relative concept: one can speak of one motion uniform with respect to the other, so that when we speak of a uniform motion, we mean motion uniform with respect to that of stars, or, though it sounds still more odiously, uniform with respect to the rotation of the Earth. Ascribing a specific, mystic sense to stellar time, one reveals the human unwillingness to understand the whole extent of the non-central, modest position of the planet where, as the fates decree, he has to live" (Friedmann 1965, p.13). The anthropomorphic selection of time scales is understandable but must not overshadow the possible application of time scales with different course uniformities in descripting various forms of generalized motion in various frames of reference.
A change of standard objects and the corresponding scale change connected with uniformity change is not just a replacement of measurement units or that of a zero point: that is necessarily a nonlinear transformation, since linear ones would preserve the scale uniformity, so that equal intervals would have remained equal. Most of "proper" time scales in natural science are non-uniform with respect to astronomical time, which sometimes allows one to discover certain laws escaping one's attention when the traditional physical time scales are used.
The scale connected with wound healing rate (Noüy 1936) turns out to be non-uniform with respect to the chronological age: a five-year-old child's wound is healed ten times faster than that of a person of fifty.
A nonlinear transformation of planetary time (Backman 1943) applied in a description of growth curves for a broad class of living organisms made it possible to discover the elementary durations, "life quanta"; their density is uniform in Backman's "organic time" and is much greater at the first stages of development from the viewpoint of the ordinary time scale (that is why it is so hard to catch them).
E.Milne (1948) removed the postulate of congruence between time intervals shown by clocks of one type, namely, mechanical and atomic ones, and introduced the logarithmic scale to measure the cosmological time of the Universe. The time transformation eliminated the gravitational interaction from the fundamental equations of motion and greatly simplified the description of the non-stationary universe.
The hypothesis of logarithmic connections among time scales. Inasmuch as the time scales determined by standards of different levels are mutually non-uniform, the question arises as to what are the functional relations among different scales. Many scientists suggest that some specific times depend logarithmically on the common physical time. Among those there are the above cosmological time due to E.Milne (1948) and G.Backman's (1943) "organic time" which parametrizes the variability of living organisms by quantitative characteristics of their growth. The size of an eye crystalline lens of a lamellidental rat Nesocia indica (as a biological age indicator) and its chronological age are logarithmically related (Shaher 1982). An attempt to use statistical methods in order to select the most adequate approximation for the dependence between the physiological age of rats, determined from 23 physiological characteristics, and their chronological age also led to the logarithmic function (Hofecker 1981).
An origin of the logarithmic law discovered experimentally for some time scale connections is one of the problems in the description of multicomponent metabolic time non-uniformity. One of the attempts to solve that problem can be found in a paper by V.S.Fleischmann (1986).
The specific nature of time scales. The times determined by standards belonging to different system structure levels and, the more so, to different natural hierarchies, are specific rather than universal.
Speaking of specific time, for instance, of physiological, ontogenetic or evolutionary times, we mean that the first one is measured by the number of absorbed oxygen molecules, the second one by the number of newly formed cells of a growing organism while the third one by the number of taxons in the reconstructed biosheric annals.
The geological, biological, geographic and other specific times are proper time pyramids constructed in the corresponding natural hierarchies.
The idea of universality of time originates from the fact that usually in a pyramid of time a sufficiently deep component is selected, corresponding to the physical time scales. Different natural systems often have a common material structure, for instance, the biological, geological, geographic, astronomical and other hierarchies include the molecular level and consequently all the previous (physical) levels. This implies the possibility to choose a unique time scale for systems of different nature. Thus the habitual universality (or absoluteness as I.Newton called it) of time is connected with the fact that only scales determined by deep levels of system structure are used. The deeper is the level which delegates the standard system, the vaster is the set of higher level systems for which that standard is applicable.
The universality of time, resulting from the use of "deep" standards, is to be paid for, and the price is the lost of information on system structure. The universality as though wipes off the structure of levels above the reference system level, therefore the characteristics of the general processes occurring at the higher levels, turn out to be insignificant.
Thus, if an ecosystem is studied as a unity of molecules, of which all the biotic components and all the inanimate substance pools consist, we can say much about the substantial functioning basis of such systems. However, the molecular language is hardly applicable for formulating the ideas of trophic connections between species, of age, sexual and other structure of the population, of seasonal and other successions, on the behaviour of individuals and other non-molecular processes.
In physics the role of a factor which "wipes up the structures", is frequently played by energy.
Using specific time scales, it is possible to explicate the properties of time determined by specific structures of systems, but the temporal properties of objects lying at lower levels of system structure become "indistinguishable". Thus the choice of a reference system level and, accordingly, of the universality and specificity degrees of the time scale determined by the chosen standard, depends on the aims of the study.
Application of specific scales, nonlinear with respect to the usual time, may result in additional simplicity and adequacy of the study to the nature of the described phenomena, along with a hope to reveal the laws which escaped attention in other ways of description.
Thus, for instance, application of the metabolic time scale, connected with the number of substrate molecules absorbed by cell populations in microalgae culture development, made it possible to discover the growth and consumption stages which had not shown themselves in any way when ordinary growth curves had been analysed (Levich et al.1986).
When the durations of development stages of animals was measured in detlafs (Dettlaff and Dettlaff 1982; see also a chapter in this book), it provided a way to compare development times both for different species and for the same species in different development conditions (e.g., at different temperatures).
The problem of the existence of individual life duration bounds is very hard to analyse if the age is measured in ordinary chronological units. Unlike that, application of a proper time, for instance, in terms of the number of molecules of matter consumed by the organism, gives a hope to discover the natural bounds connected with a limiting total amount of oxygen, absorbed by an organism in its whole life, different for different species (provided the Rubner rule is valid - see Zotin and Alexeyeva 1984).
Discreteness and additivity. Since time is determined by element replacements in systems, the course of time turns out to be discrete as far as the elements are discrete. However, the degree of discreteness of the time scale (as well as that of the system structure) depends on the choice of a reference level for time definition.
Let us call the quantity 1/N, where N is the number of elements of the reference object replaced between the appearance and disappearance of one object in the studied system, the degree of standard scale discreteness.
A replacement of one organism
(N = 1) in a population corresponds to replacements of N = 10 - 1013 of its cells or N ~ 1023 of molecules contained in the organism. Thus a choice of deep scales for time measurements drastically lowers its degree of discreteness.In a proper time scale the additivity of a substrate implies the additivity of metabolic time. If, however, at a certain structure level the discreteness and additivity of a substrate are absent (that is the case for, e.g., the psychological phenomena or objects in landscape studies and biogeocoenology), then non-additivity appears in the properties of time. In that case the element replacement concept loses its definiteness and the general process description requires a special formalism (e.g., the Boolean-valued sets theory (Levich 1982), in particular, fuzzy sets).
The existence of timeless events. If a level i object has been chosen as a time standard, then measurement of time at level i - 1 requires an introduction of fractional intervals with respect to the standard system. However, an application of fractions to the lower level can turn out to be inadequate since their "uniformity" can fail to describe processes at deeper levels. Having in hand the metabolic time construction, it is not difficult to determine both the time intervals between the events and the durations of the events themselves. In such a description a type i event turns out to be a timeless ("instantaneous") phenomenon in scales of types i and higher (but not in scales of lower types than i). For instance, if the electromagnetic time scale is chosen to be standard, all the preceding levels of system structure are excluded from the dynamical (and perhaps also causal) analysis.
Already in quantum mechanics there exist timeless events: emission and absorption of electromagnetic quanta by atoms, i.e., transitions to other energy states of atoms; wave packet reduction; changes in quantum numbers of one part of a quantum system resulting from a measurement process executed over the other, arbitrarily remote, part (the Einstein-Podolsky-Rosen paradox).
Polarization. Element replacements, forming the course of time, are of unequal value with respect to the object containing these elements: the elements can enter the system (or emerge from it), or leave the system (or die, disappear). Therefore a metabolic time interval is constructed from two qualitatively different summands:
![]() .
.
1.3. Substitutional motion
The space of states and the description of motion. It is convenient to call the set of all elements of a given type (of a single natural hierarchy level) a universum of this type (Levich 1982) - see Fig.1. In that case the space of states of a system comprising a type k object, is described by a Cartesian product of the universums of all types lower than k (it is to be noted that in the present construction the state of a system is not a point but a subset of the space of states; then, as usual, a state is a point of the phase space of states). It is also convenient to speak of the general process phenomenon with respect to the space of states as of a "generalized", "substitutional" or "metabolic" motion of the system.
A good illuminating image of such a motion is that of a "running advertisement", or a moving picture in the screen of a kinescope.
The hierarchic structure levels of a system can now play a double role - that of spatial dimensions of the world ("dimensions" are treated as components of the space of states) and that of temporal dimensions.
For instance, molecule replacements in a cell can be spoken of in the language of the time flow (an image: a stationary cage, with entering and departing molecules counting the steps of time - a "cell-centric" viewpoint). Or the same phenomenon can be spoken of as a cell's motion in the molecular space, where the word "motion" means a transition from inclusion of one environmental molecule to the cell to inclusion of another one (an image: motionless point molecules and a cell moving from one molecule to another - a "molecular-centric" viewpoint).
The conventionality principle: The choice of "spatial" and "temporal" dimensions of the world among the system structure levels is determined by an agreement among the researchers.
The metabolic motion concept, namely, that any motion of an object is reduced to "absorption" and (or) "emission" of object elements by itself (those can be "points" of the space, or medium, included in the universums of certain pre-levels of the object's hierarchic structure) - is, in my view, one of the most significant methodological consequences of the metabolic construction.
Attempting to unify the ideas of motion, one should give foundations of the extrapolation validity bounds. The suggested construction of time can be considered within the following two versions of its validity domain restrictions.
The weak hypothesis: the construction is valid only for over-molecular levels of the structure of matter. The terms like "time", "motion", "space" have only a metaphoric meaning.
The strong hypothesis: mechanical motions and the physical time are connected with element replacements at some deep hierarchic structure levels of natural systems.
The statements of the strong hypothesis can be given a much more careful sounding (preserving their heuristic role) if one refuses to endow the exchange motion and time flow with an ontological status: the exchange concept of motion (with spatial points "entering" and "leaving" a moving object) can be considered just as a convenient way of description.
A standard object - a clock - begins to play the role of a standard liner as soon as the level from which it had been delegated becomes by convention a "spatial" dimension. A time interval thus becomes a spatial distance.
It should be noted that in the metabolic construction space is necessarily a material substance, a medium. Though, that medium behaves in quite another way than the ether of the 19th century with respect to moving objects: the moving bodies have neither to "move aside" the particles of the medium thus experiencing its resistance (i.e., there is no "ether wind"), nor to carry them along to their motion; as long as the generalized (substitutional) motion of objects takes place, with respect to the pre-particles, by just replacing the pre-elements, there appears neither a resistance to motion, nor pre-particle entrainment.
The properties and equations of substitutional motion. As has been pointed out in the Introduction, a construction of time should be one of the significant components for building a dynamical theory. I would like to give an illustration of possible ways of such a development on the basis of the metabolic construction. It should be stressed that the following is just an illustration of approaches and a possible programme of studies but not a complete development.
Let us consider a hierarchic object whose variability is determined by general processes at its structure levels, as an elementary object of the theory. Constructing the I component of the theory (see the subsection "Time as a component of theoretical knowledge" in the second section of the Introduction), I would like to interpret the level of elements of the object as the spatial dimension of our model physical system and the pre-element level as the substantial reference of the system's coordinate time. The number of elements in our object is interpreted as its energy characteristic, namely, the Lagrange function L, and the number of pre-elements as the momentum p of the system. Table 1 presents the postulates introducing the connection between the numbers of replaced elements or pre-elements and changes of the just defined physical characteristics of the system. Recall that ![]() is the number of particles which entered the selected system and
is the number of particles which entered the selected system and ![]() is the number of particles which left it. I would like to note that a motion at the element level is always also a motion at the pre-element level since when elements are replaced, the pre-elements contained in them are also replaced; the reverse is not valid.
is the number of particles which left it. I would like to note that a motion at the element level is always also a motion at the pre-element level since when elements are replaced, the pre-elements contained in them are also replaced; the reverse is not valid.
Table 1.
A physical interpretation of system-theoretical concepts.|
System theory |
Natural science |
|
Object |
Physical system |
|
The element level |
|
|
Number of elements, n |
The Lagrange function L of the system |
|
Change of the number of elements in the system |
Change of the Lagrange function: |
|
The number of replaced elements in the system |
Spatial displacement: |
|
The pre-element level |
|
|
Number of pre-elements, m |
Momentum of the system, p |
|
Change of the number of pre-elements in the system |
Momentum change: |
|
The number of replaced pre-elements in the system |
Time interval: |
The theorem on an average 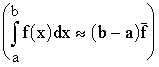 makes it possible to represent the pre-element number change in the object in the following way:
makes it possible to represent the pre-element number change in the object in the following way:
![]() .
.
![]() This formula in turn implies the relation:
This formula in turn implies the relation:
![]() ,
,
where  and
and 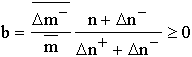 , which can be called the dynamic theorem for a metabolic object. The theorem connects the momentum variation rate of the system
, which can be called the dynamic theorem for a metabolic object. The theorem connects the momentum variation rate of the system ![]() with the "force"
with the "force" ![]() applied to it. The dynamic theorem determines the L-component of a dynamical theory of a substitutional object.
applied to it. The dynamic theorem determines the L-component of a dynamical theory of a substitutional object.
The object velocity ![]() turns out to be equal to
turns out to be equal to ![]() . If the object moves in such a way that its elements change while the pre-elements in elements are unchanged (formally:
. If the object moves in such a way that its elements change while the pre-elements in elements are unchanged (formally: ![]() and (or)
and (or) ![]() but
but ![]() ), then
), then ![]() where
where ![]() is the average
is the average 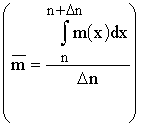 number of pre-elements in elements.
number of pre-elements in elements.
The motion of a metabolic object has the following properties:
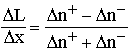 is zero and the momentum is constant (the theorem of inertia).
is zero and the momentum is constant (the theorem of inertia). .
.
![]() and
and ![]() .
.
The equation of substitutional motion is invariant under motion reversal (the motion reversal theorem). It should be noted that a "time reversal" (![]() and
and ![]() , hence
, hence ![]() ) does not leave the dynamic equation invariant but conserves the Newton equation (see the next property).
) does not leave the dynamic equation invariant but conserves the Newton equation (see the next property).
![]() .
.
Since a, b ~ ![]() ~ v, it turns out that at some substitutional object velocities new forces appear, additional to the Newtonian ones, which are proportional to those velocities and to the forces themselves (for instance, if
~ v, it turns out that at some substitutional object velocities new forces appear, additional to the Newtonian ones, which are proportional to those velocities and to the forces themselves (for instance, if ![]() , it turns out that
, it turns out that ![]() ). The equation of motion is hereby non-invariant under time reversal. Experimental interpretations of these additional forces are discussed in the second volume of the present book.
). The equation of motion is hereby non-invariant under time reversal. Experimental interpretations of these additional forces are discussed in the second volume of the present book.
![]() ;
;
![]()
where the corrections a, b, c, d and others estimate the intensity of "internal" motions in elements compared with the intensity of object motion at the element level.
1.4. Difficulties of the substitutional approach
1. When a system is composed of several sorts of elements, one needs additional considerations to choose the particle sorts or combinations of sorts in order to define the proper time scale. A similar question arises if a system consists of several subsystems where element replacements are not synchronized.
The life of a cell is connected with replacements of molecules including many chemical elements and their replacement rates are drastically different. A metabolic clock of a cell can be defined via the so-called "limiting" element, or a sum of all sorts of molecules, which is convenient in certain cases and unsatisfactory in others.
The cells of an organism are differentiated, so that cell replacement rates in different tissues, subsystems and organs are not equal. Thus, which are the cells whose replacements count the biological age of an animal, epithelial, neurons or erythrocytes?
The existence of structure in natural systems forces one to use for their formal description sets with determined mathematical structures (relations, operations, topologies...). The metabolic approach implies an ability to count element numbers in objects. Therefore, when the metabolic construction is used for structured sets, one needs to generalize accordingly the concept "the number of elements".
2. The metabolic approach has its elementary object, the space of states, there is a way to idealize the variability along with its quantitative parametrization. However, a principle for finding out the system variability law has not been formulated. (The equation of metabolic motion, obtained in the previous section, has its base in a conjecture rather than in a systematic derivation rule.)
The subsequent sections suggest some ways of dealing with some of the above difficulties.
3. The metabolic construction implies the ability to fix the fact that a certain element belongs to a certain object or not, along with the ability to count the number of elements in objects and to reveal its changes. Mathematically, sets theory begins when the question of belonging or non-belonging of elements to sets has been solved. Unlike that, natural science needs an operational procedure providing a practical (or principle) possibility of solving the problem of belonging. The ability to count element numbers in sets is provided by the existence of single-valued or multi-valued mappings between the sets. Thus, while in a mathematical theory such mappings must exist in principle, their existence in natural-scientific interpretations should be provided by operational, or experimental, procedures. The necessary procedures can possibly be constructed on the ways of generalizing the natural-scientific concept of a "signal".
4. The variability principle determines the construction of events as system element replacements. An additional postulate is hereby required, introducing the order relation on the set of events. The necessary ordering principle is implicitly introduced when a standard object is chosen: It turns out that, for any time standard, element replacements (more generally, simultaneous replacements of certain sets of elements) are ordered in our experience. So far the metabolic approach has no construction which could provide a natural introduction of the ordering principle.
2. The entropy parametrization of time and the extremum principle for motion
All the real systems are explicated in formal descriptions by structured sets, therefore to apply the metabolic approach one needs to be able to count the number of replaced elements in structured sets.
2.1. Numbers of elements in structured sets
Categories instead of sets. Application of a mathematical formalism in theoretical knowledge begins with selection of an elementary object of the theory, i.e., a certain set, structured in one or another way.
An ecological community of individuals belonging to different species can be well described by the structure of a partitioned set with classes corresponding to populations which form the community.
The proximity and remoteness concepts in the empirical space are described by the topological structure.
The aggregate of atomic states can be described in terms of vectors in the infinite-dimensional Hilbert space or, equivalently, by the field of infinite matrices.
A language has been created in mathematics for describing arbitrary structured sets, namely, category and functor theory. An elementary entity in category theory is not a "frozen" state of a natural object (as is the case in sets theory) but a transformation, a "motion" of an object, or a morphism in the category-theoretic language. A category is a more general concept than a set: only some categories at certain conditions become aggregates of sets.
Cardinalities instead of quantities. A consistent presentation of the ideas concerning the cardinal structure of sets and its possible generalizations can be found in a book specially dedicated to natural-scientific applications of category theory (Levich 1982). All the statements used as a basis in the subsequent presentation, which is to a maximum extent unformal, were proved there.
There are two ways to compare the quantities of elements in sets. Let us say, we must find out, whether or not there are enough chairs for the people gathered in the room. One can count separately the number of chairs and the number of people and compare the two numbers. Or one can ask each person to sit down alone on a single chair. As soon as all the people take their seats, we shall be able to know, without counting either chairs or people, which of the quantities is larger: it is sufficient to know, whether there remained empty chairs or standing people. In mathematics such a way of comparison is called to establish a correspondence (or a mapping) between two sets. The second way of comparison is more fundamental than the first one since the construction of a number of elements is built on the basis of establishing correspondences between sets.
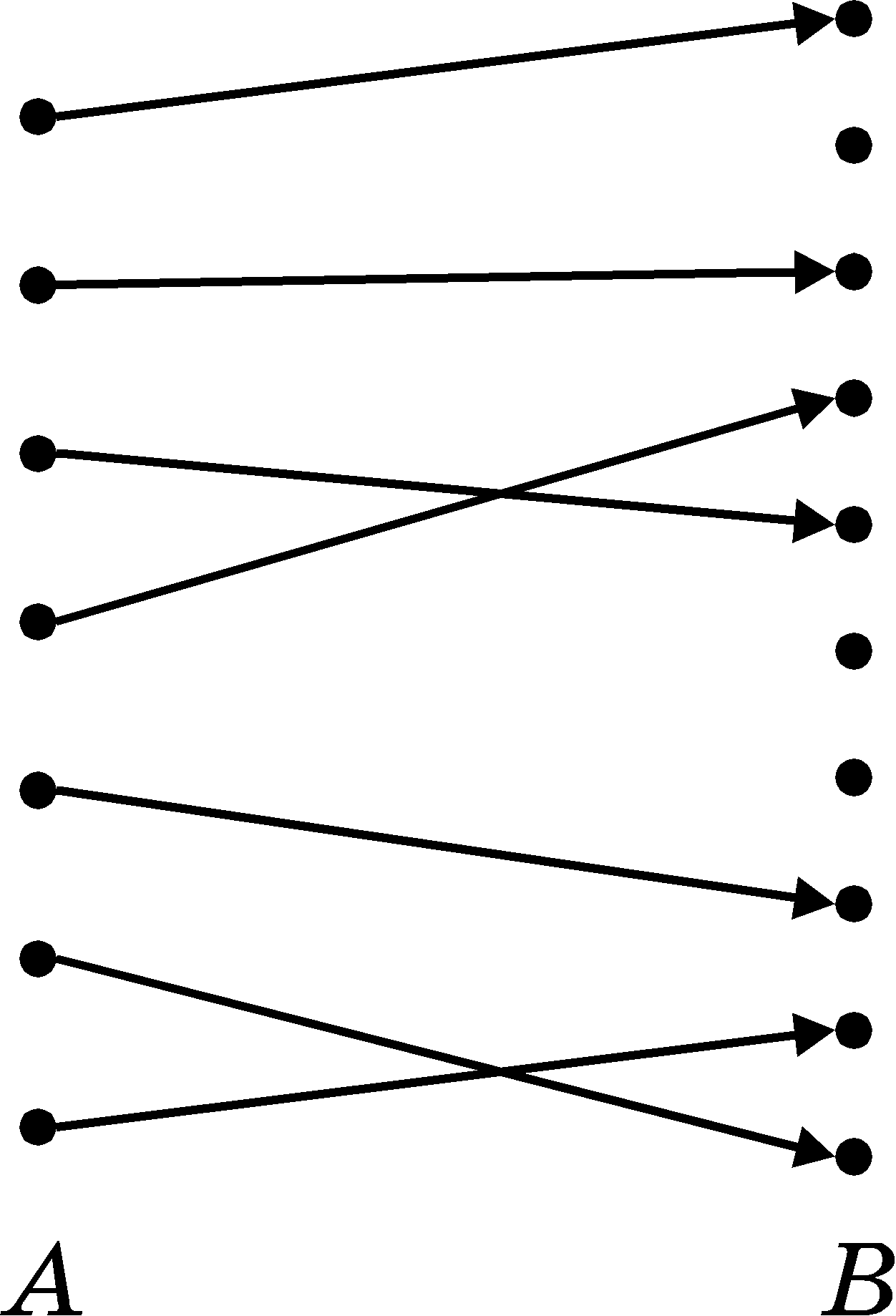
Let us mark correspondences between elements of sets by arrows. If a single arrow leaves each element of set A and no more than one arrow enters any element of set B (Fig.3), then such a correspondence from A to B is called an injection. If there exists an injection from A to B (one man is sitting on each chair and nobody has occupied several chairs at once), we say that the number of elements of set A is less then of equal to that of set B. If there exist injections both from A to B and from B to A, then the numbers of elements in these sets are equal. As long as correspondences enable one to compare both finite and infinite sets, one uses the term "equicardinality" instead of "equal numbers of elements" and the term "cardinality" instead of the term "number of elements". The natural numbers, being the cardinalities of finite sets, become just the names of the equicardinal sets corresponding to each other.
Structure strength. Consider some examples of structured sets.
1. Partitioned sets. Certain properties of elements are indicated which make them equivalent. Groups of equivalent elements form non-intersecting classes into which the whole set is divided.
A community of living organisms which inhabit a certain location, for instance, all the individuals living in a pond; a whole set of indications divides them into populations belonging to certain biological species.
The set of natural numbers is divided into classes, for instance, giving the same remainder after division by 3:
N = k0 È k1 È k2 where k0 = {3, 6, 9, 12, ...}, k1 = {1, 4, 7, 10, ...} and k2 = {2, 5, 8, 11, ...}.2. Sets with composition laws. Any two elements, a and b, of such a set determine a certain third element c called their composition.
In the set of whole numbers any two elements determine the third one, their sum.
In Boolean algebra with the two-dimensional truth space {truth
(t), lie (l)} a number of logical operations (composition laws) are defined. Examples:|
conjunction: |
Ù |
t |
l |
or disjunction: |
Ú |
t |
l |
|
t |
t |
l |
t |
t |
t |
||
|
l |
l |
l |
l |
t |
l |
3. Metric spaces. Any two elements a and b determine a number S (a, b) such that S (a, a) = 0, S (a, b) = S (b, a) and S (a, c) £ S (a, b) + S (b, c).
For points ![]() and
and ![]() in the three-dimensional Euclidean space the metric is defined by
in the three-dimensional Euclidean space the metric is defined by
For structured sets, among all the possible correspondences those preserving the structure of sets, are selected. These correspondences are called morphisms of the structure.
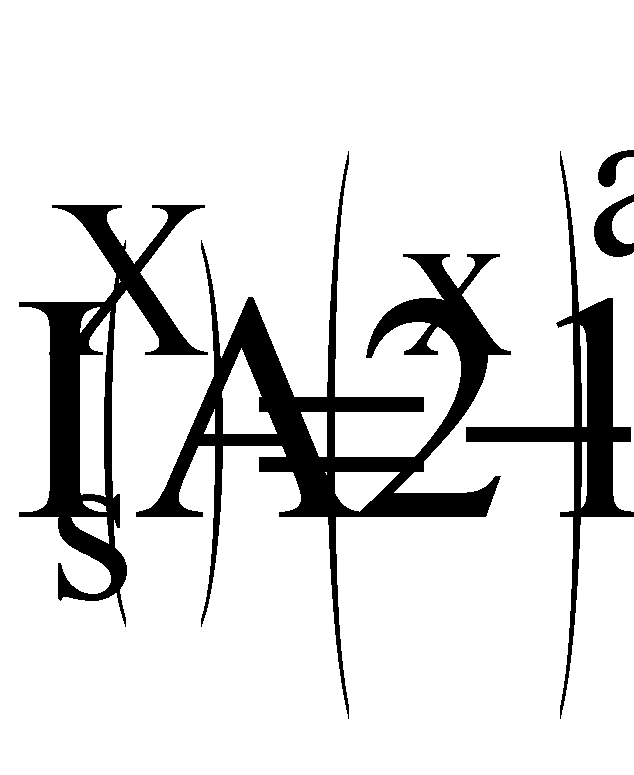
For an ecological community morphisms conserving partition into species, are transformations consisting of individual births and deaths. These transformations transfer a species into itself.
For arbitrary partitioned sets morphisms by definition are those correspondences which do not mix the classes of equivalent elements. Thus, for the number divisibility relation a morphism is any number-valued function of the form
y = n x where n is a natural number (for instance, if x1 and x2 have equal remainders after division by 3, then the corresponding y1 and y2 will have equal remainders too).For whole number addition an example of a morphism is the transformation
y = -x, changing the sign of a number: a + b = c, hence, -a + (-b) = -c.For the metric structure one of the morphisms is a transformation of rotation in the three-dimensional space, since rotations conserve the spatial metric.
Quantitative comparisons between unstructured sets can be easily generalized to include sets with equal structures. The structure of set A is considered to be weaker than that of set B if an injective morphism of structure from A to B exists. For example, the partition of set A in Fig.4 turns out to be weaker than that of set B.
In the same manner as the comparisons of unstructured sets with injections create the concept of the number of elements in a set (natural numbers, cardinalities), comparisons of structured sets with morphisms create structure numbers of those structured sets. Numbers of elements can be compared for any sets since the trichotomy principle is valid for any two sets: either the number of elements in A is greater than that in B, or conversely, or those numbers are equal. Thus either an injection from A to B exists, or from B to A, or both. As far as the structure numbers of structured sets are concerned, the ordering is only partial: there exist pairs of structured sets for which neither a direct, nor an inverse injection preserving the structure, exists. Fig.5 shows an example of partitioned sets between which there are no injective morphisms. Thus if structure numbers are used as a basis for variability parametization, the resulting time would look exotically: its instants are only partially, rather than linearly, ordered.
Structure comparisons by functors. The partial order of structured sets, along with the technical difficulty of finding injective morphisms for some structures, make one continue the search of new ways to compare structured sets quantitatively. There is a way well elaborated in mathematics where the search could be lucky. That is, the way of representing some mathematical structures by other mathematical structures.
The rotation properties of the geometric space can be effectively studied using products of certain matrices.
The whole measure theory, including measurements of lengths, areas and volumes in geometry, is an example of quantitative parametrization built on the basis of representations of geometric structures into the numerical structures of the analysis.
Equivalent mathematical descriptions are frequent in physics: atomic states in quantum mechanics can be described both by vectors in the infinite-dimensional Hilbert space (the Schrödinger approach) and by infinite matrices (the Heisenberg approach).
The aspect of interest for us here is that of quantitative comparison of equally structured sets and we have to deal to a greater extent with morphisms of their structures than with the sets themselves. Therefore it will be convenient to give further presentation in the language of category theory, specially destined to describe the aggregates which include structured sets and their morphisms on equal rights.
A category includes a class of objects and sets of morphisms determined for some (or all) pairs of objects. A composition law and a number of axioms for morphisms have been formulated which make morphisms look like mathematical correspondences between sets. The clearest examples of categories are the aggregates of equally structured sets:
A functor is a mapping of one category to another, which transfers objects to objects, morphisms to morphisms and necessarily preserves compositions of morphisms. The functors turn out to be representations of structures of one category by structures of another.
Selected morphisms of a category create ordering of its objects. Thus, in the preceding paragraphs we compared structured sets using injective morphisms. If a functor representation is monotonic with respect to ordering in categories ("the structure of object A is stronger than that of object B in category S1" implies that "the structure of object F (A) is stronger than that of object F (B) in category S2", where F is a functor from S1 to S2), then presentation of a monotonic functor is the functor method of comparing structures. Namely, one can judge object ordering in some category with a complicated and unusual structure (say, objects A and B) by ordering of their images F (A) and F (B) in a category with a simple or well studied object structure (in the cited book (Levich 1982) sufficient conditions for functor monotony are presented).
Invariants of structures. When structured sets are ordered by injections, there is a functor from an arbitrary category of structured sets to the category of unstructured sets which turns out to be monotonic. That is the functor which puts into correspondence to each object A the set of all morphisms Hom (X, A) from a fixed object X to the object A. Thus if the structure of object A is stronger than that of object B, the number of transformations of an arbitrary object X to A which preserve the structure, is greater than the number of such transformations from object X to object B. If the structures of objects A and B are equal, then the numbers of transformations in the sets Hom (X, A) and Hom (X, B) are also equal. Therefore the number of transformations in the set Hom (X, A) is conveniently called an invariant of structure of object A with respect to object X and is denoted by IX(A).
It should be noted that if ![]() are invariants of object A for several Xj , then the sum
are invariants of object A for several Xj , then the sum ![]() also has the properties of an invariant.
also has the properties of an invariant.
If structured objects are comparable, then their invariants are ordered in the same way as the objects. However, we know that structured sets can turn out to be incomparable. In that case the principle of continuation of structure ordering by ordering of their invariants can be useful: the structure of object A is considered to be stronger than that of object B (with respect to object X) if IX(A) ³ IX(B).
The functor comparison of structures can be treated as a further generalization of the concept of quantity: from the quantities of elements of structureless sets (determined by comparison using injections), via the structure numbers of structured sets (determined by comparisons of sets using injective morphisms of structures), to the numerical invariants of structure. Apparently, the described constructions are not the only way to generalize the concept of quantity (see Sharov 1977). One can try to find other functors to the category of sets, or choose another parametrizing category instead of the category of sets, or choose other special sort of morphisms to compare objects in the initial category instead of injections (and, accordingly, another functor to the parametrizing category), etc.
I would like to give an example of structure comparison with the aid of invariants. Let us consider the structure of partitioned sets. The morphisms which transfer each partition class of one set as a whole to a certain unique class of another set, are admissible. If ![]() is class i in the partition of set X and
is class i in the partition of set X and ![]() is the partition class of set A into which class i is transferred, then the entire number of morphisms is
is the partition class of set A into which class i is transferred, then the entire number of morphisms is
![]() .
.
If the morphisms are mappings and class Ki contains ni elements, then
![]() .
.
If, instead of class-to-class mappings, some arbitrary class-to-class correspondences are admissible, then the expression for an invariant preserves its form of a product over classes, but with altered multipliers. I would like to present the expressions for the multipliers for all possible combinations of the canonical properties of correspondences (Table 2).
It should be noted that the invariants of many (and maybe any) mathematical structures are expressed in terms of partitions associated with these structures, therefore their invariants have the characteristic form of products of invariants for separate partition classes. This remark will be useful when we turn to discussing the ways of calculating the entropy of systems.
2.2. A category description of systems
The O, C and S components of a theory. Assume that a natural system is described by a certain chosen mathematical structure; assume, further, that some consistent considerations determine the transformations admitted by the structure of the system. Let us consider the category Q of structured sets where the mathematical structure, defined on the sets, explicated the system properties.
Let us identify the system states with the objects of the category and mutual transformations of the states with the morphisms of the category. In the language of methodology of theoretical descriptions of natural systems (see the Introduction) an elementary object of the theory is now a structured set; the system variability is presented by morphisms which transform objects to other objects; the space of states is the object aggregate of category Q.
Table 2.
There are the numbers of correspondences from set X (number of elements is x) to set A (number of elements is a). CK denotes a set consisting of k elements. Lower indices mean that the number of correspondences is counted with the properties whose notations are contained in the indices, namely:p - correspondences defined everywhere;
f - functional correspondences;
i - injective correspondences;
s - surjective correspondences.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
It can be noticed that a category-theoretic description of systems does not necessarily require an explication of a natural system by a mathematical structure. One can have a “qualitative” category description of systems, i.e., the system states can be enumerated and described, along with all transformations between states (morphisms), not in the mathematical language but in some internal language of the relevant field of knowledge.
To obtain a formulation of a full dynamical theory it only remains to determine its T and L components, i.e, the variability parametrization method and the variability law.
Entropy of systems. Let us introduce the entropy of a state A with respect to a state X in terms of the invariants of structured sets in the following way:
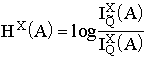 . (2.1)
. (2.1)
Here Q is the category of structured sets and ![]() is the category of sets with a "wiped off" structure. X marks the states of a system belonging to its certain macrostate (the concept of a macrostate is introduced in the subsequent paragraphs). The entropy of a whole macrostate is determined by a proper summation over all X.
is the category of sets with a "wiped off" structure. X marks the states of a system belonging to its certain macrostate (the concept of a macrostate is introduced in the subsequent paragraphs). The entropy of a whole macrostate is determined by a proper summation over all X.
Expression (2.1) for the entropy can be interpreted as a measure of structuredness of state A, i.e., a measure of a deflection of the structure of state A from its structureless counterpart.
This expression generalizes the traditional ways of introducing entropy to statistical physics. Commonly the entropy of a system is defined as the logarithm of a specific number of its different microstates corresponding to its given macrostate. I would like to interpret a macrostate as a class of states among which transformations are admissible from some consistent considerations, for instance, some system macroparameters are conserved (energy, particle number, etc.), while a microstate is a result of an arbitrary transformation of the system.
Thus to calculate the entropy of a system it is necessary to calculate the number of its transformations-morphisms, ![]() . This number depends on both the system structure and the number of elements contained in it. The multiplier
. This number depends on both the system structure and the number of elements contained in it. The multiplier ![]() has been introduced in order to normalize the entropy to a single element of the system, i.e., to introduce a specific invariant of structure.
has been introduced in order to normalize the entropy to a single element of the system, i.e., to introduce a specific invariant of structure.
The "entropy-like" functions of system state, having appeared in thermodynamics, have penetrated via statistical physics, information theory and cybernetics to the quantitative methods of a wide range of sciences. The success of its applications is entirely determined by the possibilities of calculating the entropy in the cases of interest for the researcher. The purely thermodynamic approaches to calculating the entropy are very restricted: "... a formulation of the second law from a modern physicist's viewpoint is a programme rather than a statement admitting an unambiguous interpretation, since neither Thompson nor Clausius indicated a precise procedure of expressing an entropy variation in terms of observed quantities" (Prigogine 1986, p.93). Only Boltzmann's interpretation of entropy through the number of ways to reach a given macrostate of the system yields a constructive way of calculation. Its interpretation in terms of the number of morphisms gives further possibilities for calculations.
As it has already been mentioned, the invariants of many (if not all) mathematical structures are expressed in terms of the invariants of partitions associated with the structures. The invariants of partitioned sets are multiplicative with respect to invariants of each partition class, therefore the logarithms of invariants involved in the entropy, are additive and have the characteristic "entropy-like" form of sums over partition classes.
The entropy expressions are obtained apart from any statistical prerequisites. For instance, if the admitted morphisms are mappings, then the expression
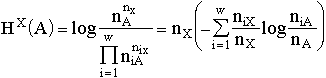 ,
,
where 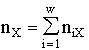 and
and 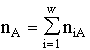 , is valid for all, even very small, n. Introducing
, is valid for all, even very small, n. Introducing ![]() and representing the set of values pi as a distribution function for a state A, one can interpret the entropy formula as a generalization of Boltzmann's H-function
and representing the set of values pi as a distribution function for a state A, one can interpret the entropy formula as a generalization of Boltzmann's H-function
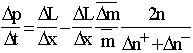 ,
,
which (Prigogine 1985, p.303) serves as a probability measure of the deflection of a system's state at an instant t from its equilibrium state.
It should be noted that the entropy expressions given in the present section as examples (as well as the generalizing invariant expressions of Table 2) correspond to the simplest (two-level) systems. In the problems where greater numbers of hierarchic levels of systems are significant, it becomes necessary to calculate invariants for hierarchic structures (e.g., for the armade structure - Levich 1982).
2.3. The extremum principle as a law of variability
In natural science an equation of motion is usually a postulate, generalizing the experience of mathematical descriptions of a certain piece of reality, and invented by a genius whose name becomes that of the equation. There is another way of obtaining the equations: to replace a postulate in the form of an equation by a postulate in the form of a functional. We are speaking of the extremum principles of natural science, claiming that only those states of systems take place in the reality for which a given numerical function (functional), whose argument contains the trajectories of motion, takes extreme values.
If an equation of motion is known, it can be a standpoint for determining the form of the functional whose extremal would be the above equation. And conversely, if a functional is given, the variational method of finding its extremum leads to the equations of motion. Thus building of dynamics from postulated equations and postulated functionals leads to the same results. However, the extremum principle has a greater heuristic and generalizing power.
Why does a stone thrown at an angle to the horizon, move along a parabola? Explaining the phenomenon, one can mention the uniformly accelerated motion law ![]()
![]() . That law itself is a consequence of Newton's second law
. That law itself is a consequence of Newton's second law ![]() for a body subject to a constant force; in other words a parabola can be described as a geodesic line from a solution of the Einstein equations of general relativity applicable for motions in strong fields and at high velocities. Newton's law, as well as the Einstein equations, can be derived from the minimum action principle with a certain form of the functional to be minimized. Thus there are a few levels of explanations for the phenomena and each of them can serve as an initial postulate. However, the uniformly accelerated motion law corresponds to just a narrow class of phenomena, Newton's second law describes all motions in weak fields with low velocities, the Einstein equations are already free of these restrictions, while the minimum action principle is applicable to all the forms of mechanical and electromagnetic motions.
for a body subject to a constant force; in other words a parabola can be described as a geodesic line from a solution of the Einstein equations of general relativity applicable for motions in strong fields and at high velocities. Newton's law, as well as the Einstein equations, can be derived from the minimum action principle with a certain form of the functional to be minimized. Thus there are a few levels of explanations for the phenomena and each of them can serve as an initial postulate. However, the uniformly accelerated motion law corresponds to just a narrow class of phenomena, Newton's second law describes all motions in weak fields with low velocities, the Einstein equations are already free of these restrictions, while the minimum action principle is applicable to all the forms of mechanical and electromagnetic motions.
The extremum principle: For natural systems described by mathematical structures,the extremum principle is suggested in the following form: a system passes from a given state X to another state A for which the entropy ![]() is maximum within the limits admitted by the conditions of system functioning (e.g., the available energy or other resources).
is maximum within the limits admitted by the conditions of system functioning (e.g., the available energy or other resources).
Thus, in the language of category-theoretic descriptions of systems, the L component of the theory appears.
In the present context entropy is not an initial, undefined concept but an exact construction. This suggests additional interpretations to the extremum principle:
1. By definition, the entropy ![]() is considered as a measure of remoteness of the structured state A belonging to category Q from its counterpart belonging to category
is considered as a measure of remoteness of the structured state A belonging to category Q from its counterpart belonging to category ![]() with a "wiped off" structure. According to the extremum principle, those states are realized which are most remote from their entirely structureless counterparts, i.e., more structured than the others.
with a "wiped off" structure. According to the extremum principle, those states are realized which are most remote from their entirely structureless counterparts, i.e., more structured than the others.
2. In the entropy formula the denominator ![]() is an invariant of the structured set A. The inequality
is an invariant of the structured set A. The inequality ![]() means that the structure of set A is weaker than that of set B (with respect to object X), in the sense of the order relation "structure strength". Assume that for two system states A and B the numerators
means that the structure of set A is weaker than that of set B (with respect to object X), in the sense of the order relation "structure strength". Assume that for two system states A and B the numerators ![]() in the entropy formula are equal, i.e., the states A and B are different realizations of a certain structure at equicardinal basic sets, e.g., different partitions of the same set, or groups which are equicardinal as sets. Then the maximum entropy and the real state correspond to a minimum (by structure strength) state of the system. Thus entropy plays the same role as the invariants of mathematical structures: it orders the structures themselves along with natural system states described by them.
in the entropy formula are equal, i.e., the states A and B are different realizations of a certain structure at equicardinal basic sets, e.g., different partitions of the same set, or groups which are equicardinal as sets. Then the maximum entropy and the real state correspond to a minimum (by structure strength) state of the system. Thus entropy plays the same role as the invariants of mathematical structures: it orders the structures themselves along with natural system states described by them.
3. On the example of partitioned sets (so that morphisms are bijections) one can see that the entropy  is maximum if the following two conditions are simultaneously valid: the number of elements of the system (the numerator) is maximum while the number of transformations preserving the structure (the denominator) is minimum. A small set of transformations admitted by the system structure can be treated as a high stability of the state. As for the extremum principle, it realizes both a maximum expansion of the elements of the system and its most stable state.
is maximum if the following two conditions are simultaneously valid: the number of elements of the system (the numerator) is maximum while the number of transformations preserving the structure (the denominator) is minimum. A small set of transformations admitted by the system structure can be treated as a high stability of the state. As for the extremum principle, it realizes both a maximum expansion of the elements of the system and its most stable state.
4. Note that without additional restrictions the maximum expansion requirement, created by the extremum principle, leads to an infinite growth of the number of elements in the system. The life of natural systems is always connected with limited resources (energy, substrates, space, information, etc.). For instance, for substrate and energy factors these restrictions can be written formally as the balance inequalities
![]() , (2.2)
, (2.2)
where ![]() are functions of a state and
are functions of a state and ![]() are resources consumed by the system in its expansion. Therefore the real states of systems are solutions of conditional extremum problems.
are resources consumed by the system in its expansion. Therefore the real states of systems are solutions of conditional extremum problems.
It can be shown that the entropy extremum principle with resource-factor restrictions (2.2) is equivalent to the minimum consumption principle with respect to any of the limiting resource factors, with restrictions taking into account the minimum admitted value of the entropy characteristic of the system.
5. Both mentioned variational problems are equivalent to an unconditional extremum problem (with the same Lagrange function for both problems). For instance, the problem "the entropy ![]() is maximum,
is maximum, ![]() , where E is the system energy" is equivalent to the unconditional minimum problem for the functional
, where E is the system energy" is equivalent to the unconditional minimum problem for the functional ![]() where d is a Lagrange multiplier. Recall that in statistical physics for perfect gases the Lagrange multiplier turns out to be inverse proportional to the temperature, d = - 1/T , and the relation F = 1/T (E - TH) is valid. In such a condition the extremum principle is treated as that of minimum free energy of a system.
where d is a Lagrange multiplier. Recall that in statistical physics for perfect gases the Lagrange multiplier turns out to be inverse proportional to the temperature, d = - 1/T , and the relation F = 1/T (E - TH) is valid. In such a condition the extremum principle is treated as that of minimum free energy of a system.
6. The entropy of a system expressed in terms of the invariants of the corresponding mathematical structures, can be interpreted as the amount of information connected with the system structure (Levich 1978). Therefore the above extremum principle can also be interpreted in terms of information.
In the subsequent sections other interpretations of the extremum principle are also discussed: the maximum ecological variety, a comparison with the second law of thermodynamics, the aspects of growing system complexity and self-organization.
Has one to interpret the extremum entropy principle just as that of inevitable entropy growth to its maximum? G.E. Mikhailovsky singles out the world of the existing (Laplace's), with a stationary entropy value, the world of the emerging (Prigogine's), with entropy growing along the real trajectories due to dynamic instabilities, and the world of the developing (the world where the equifinality principle governs), with negative entropy increments; he ascribed the essentially biological and social systems to the world of equifinality.
The extreme structure realization principle put forward in the present paper is certainly open for further generalizations and new interpretations.
The appearance of entropy in the present context has some peculiarities compared with situations in which entropy has repeatedly occurred in different fields of natural science:
2.4. Example: a formula of species structure in ecology of communities
Let us describe an ecological community by the structure of partitioned sets: the elements of sets are individuals, the partition classes are populations of biological species. A state of the community is the vector ![]() whose components
whose components ![]() are the numbers of individuals ("sizes") of each of the w constituent species.
are the numbers of individuals ("sizes") of each of the w constituent species.
Fig.6 shows the transformations occurring with the biological organisms and their mathematical interpretation.
Let us specify the model for a community of organisms of the same trophic level, for instance, for a phytoplankton community without cell introduction from outside. Phytoplankton cells do not absorb their counterparts and do not merge; besides, the species do not interact with each other genetically or trophically. Therefore the admitted transformation are not necessarily everywhere defined (mortality), not always functional (cell fission), but surjective (no introduction) and injective (no cell merging) correspondences of each partition class into itself (absence of interaction between species).
Note that the model of a community is determined not only by the explicating mathematical structure (partitioned sets), but also by admitted morphisms. A choice of other morphisms for the same structure would create another model. Thus, bijections chosen as admitted morphisms would lead to the existence of states with only constant sizes of species. As illustrated below, changed properties of allowed morphisms drastically change the character of species size distribution. Therefore the present model is essentially category-theoretic rather than just using the language of that theory.
The functional, whose maximization is to determine the dynamics of the community according to the extremum principle, for the chosen admitted morphisms, has the following form:
![]()
 , (2.3)
, (2.3)
where 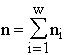 is the total number of cells in the community.
is the total number of cells in the community.
Let us also note that here we have used the global formulation of the extremum principle rather than the local one: we are looking for a final stationary state of the system for which only the entropy of a transition to itself is extreme, i.e., ![]() .
.
The community lives at the expense of the environmental resources which restrict the infinite expansion of species. Thus a real state of the community ![]() is an extremal of the variation problem
is an extremal of the variation problem
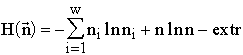 ;
;
 . (2.4)
. (2.4)
Here ![]() and
and ![]() is the requirement of the species i of the resource k,
is the requirement of the species i of the resource k, ![]() and
and ![]() is the quantity of the resource k present in the medium.
is the quantity of the resource k present in the medium.
The problem has the solution
![]() ,
,![]() (2.5)
(2.5)
where ![]() are the Lagrange multipliers found together with n from the algebraic equations
are the Lagrange multipliers found together with n from the algebraic equations
![]()
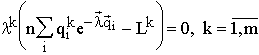
![]() . (2.6)
. (2.6)
It should be pointed out that such a solution is unique and always exists (Levich et al. 1994).
The species structure formula (2.5) adequately describes the empirical sizes of species in ecological communities (Lurie 1983; Gavrilov et al. 1986; Levich et al. 1986b; Levich et al. 1993a).
An analysis of the formula (2.5) has made it possible to draw a theoretical conclusion (and to confirm it by experimental studies) that the relative size of a given species takes its maximum value when the resource factor ratios in the medium is equal to the requirement ratios for the above species.
In one of the most recent works (Levich et al. 1994) the "limiting link rule" has been proved for the problem (2.4). The rule generalizes Liebig's minimum principle and Mitscherlich's combined action law for the environmental factors: the space of the consumed factors is decomposed ("stratified") into 2m - 1 non-intersecting subsets, with a unique collection of consumed factors for each of them, so that in that subset they and only they
a) are consumed entirely,
b) are the arguments of the extremal (2.5).
Let us illustrate the potentialities of the method by choosing other admitted transformations. Assume that arbitrary correspondences are admitted, i.e., that, apart from deaths and reproduction, introduction of individuals and absorption of organisms by other organisms are admitted. A solution of the problem
 ,
,
![]() (2.7)
(2.7)
is the extremal
![]() .
.
It should be noted that the functionals (2.4) and (2.7) are applied in ecology irrespective of the described approach and are called species structure variety indices of ecological communities (Levich 1980). Thus the extremality of the functional H which creates the community dynamics, can be interpreted as the requirement that the variety of a system should be maximum possible in the condition of the restricted available resources.
Let us point out more precisely, which sort of dynamics is spoken of: the variability of a species size (number of individuals) ![]() parametrized by the amount
parametrized by the amount ![]() of the consumed substrates. Indeed, the sizes
of the consumed substrates. Indeed, the sizes ![]() depend, by (2.5), on the multipliers
depend, by (2.5), on the multipliers ![]() , which, according to (2.6), are, as well as the total number n, functions of only the resource flows through the community
, which, according to (2.6), are, as well as the total number n, functions of only the resource flows through the community ![]() . Thus the dynamics in terms of the substitutional time of the system is implied.
. Thus the dynamics in terms of the substitutional time of the system is implied.
2.5. The substitutional, entropy and category time
The substitutional time has been defined as the number of elements replaced in the system. The entropy time is connected with the number of transformations of the system. Since (according to the variability unification principle) the transformations consist in just element replacements, at a qualitative level a relation between the metabolic and entropy times is evident. However, there is an unambiguous quantitative relation between them. Let us illustrate it on the example of the variational problem (2.4) of the previous section. The entropy ![]() where
where ![]() , taking into account that
, taking into account that ![]() and
and ![]() , is converted into
, is converted into 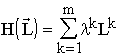 where the Lagrange multipliers
where the Lagrange multipliers ![]() are also
are also ![]() -dependent. The connection between the entropy and the metabolic time components is strictly monotonic since it can be shown that
-dependent. The connection between the entropy and the metabolic time components is strictly monotonic since it can be shown that ![]() (Levich et al. 1994).
(Levich et al. 1994).
Note that if one of the factors ![]() which is significant for the functioning of the system is the heat
which is significant for the functioning of the system is the heat ![]() , then the corresponding Lagrange multiplier
, then the corresponding Lagrange multiplier ![]() is 1/T where T is the absolute temperature. This implies that the thermodynamic entropy
is 1/T where T is the absolute temperature. This implies that the thermodynamic entropy ![]() , as well as Boltzmann's statistical entropy, is a particular case of the category definition of entropy.
, as well as Boltzmann's statistical entropy, is a particular case of the category definition of entropy.
The relation ![]() demonstrates an important result: entropy plays the role of an "averager" of metabolic times of a system with several sorts of replaced elements. The Lagrange multipliers play the role of metabolic "eigenfrequencies" of the system. Thus the entropy parametrization solves the problem of different sorts of elements in universums, emerging in the metabolic approach.
demonstrates an important result: entropy plays the role of an "averager" of metabolic times of a system with several sorts of replaced elements. The Lagrange multipliers play the role of metabolic "eigenfrequencies" of the system. Thus the entropy parametrization solves the problem of different sorts of elements in universums, emerging in the metabolic approach.
The entropy parametrization has appeared due to a mathematical trick: system structure ordering was replaced by number ordering. Therefore one can say that the entropy parametrization is secondary with respect to the way of system ordering by homomorphisms. In the above formalism we have compared the systems using monomorphisms (similar to injections for comparisons of unstructured sets). In general, structures can be compared with other morphism choices than monomorphisms in the category. In addition to the main single-place functor which has created the entropy, other functors can also be monotonic with respect to structure ordering, or it may turn out that there are no such functors. Thus time parametrization by structure numbers (let us call it category time) is a more general construction than the entropy method. However, as it has been mentioned, the structure numbers are only partially ordered, therefore the time introduced by them has rather exotic properties.
The entropy (and, accordingly, metabolic) times are brought to an agreement with structure ordering with the help of injective morphisms (i.e., embeddings). Therefore, according to the extremum principle, the evolution of a system proceeds from subobjects to objects and further to super-objects. Such an evolution can be called conservative or causal: the achieved states do not disappear (a subobject is "conserved" in an object), while new states emerge not on a blank space but from their "weaker" predecessors (in the sense of ordering by "structure strengths").
If one refuses to use monomorphisms as ordering morphisms in describing a certain system, it may lead to alteration of the just formulated principle of conservative evolution of natural systems. Apparently the choice of ordering morphisms is a matter of explication of the operational ways of establishing the belongings of elements to objects. The concept of a signal can apparently be a natural-scientific interpretation of the ordering morphism construction.
The theorem of category theory establishing the monotony of structure ordering and their entropy invariants (Levich 1982, p.113) actually plays the role of Boltzmann's H theorem, since the former also proved the monotony of entropy but in category time instead of the physical one. The above monotonic connection between the entropy and metabolic times plays a similar role.
Since in the course of system variability its metabolic time interval ![]() strictly increases, the system entropy also increases along its trajectory in the space of states. That means that entropy can be used to parametrize the variability, or to determine a quantitative measure of changes in its states. Thus the T component of the category-theoretic description of systems appears, which can be called the entropy time of systems.
strictly increases, the system entropy also increases along its trajectory in the space of states. That means that entropy can be used to parametrize the variability, or to determine a quantitative measure of changes in its states. Thus the T component of the category-theoretic description of systems appears, which can be called the entropy time of systems.
As it has already been pointed out, in the development of a dynamical theory for a certain fragment of reality one has to solve a number of concrete methodological problems: to construct an elementary object of the theory, to enumerate the allowed states of objects and the ways of their variability, to construct the ways to parametrize the variability and, finally, to formulate the variability law which should select the real generalized motion of objects in the space of states from all the possible ones. The results of the present chapter suggest the following:
As elementary objects - a hierarchy of structured sets which are open with respect to element substitution at some levels of the hierarchy.
As the space of states - a category whose objects (the elementary objects of the theory) are interpreted as states of the studied system while the morphisms as the ways of system variability.
As a clock - variability parametrization given by the entropy of system states, calculated via the values of a one-place functor of the categories. The entropy parametrization is co-monotonic with the metabolic one, determined by the number of elements replaced in the system.
As the variability law - the maximum entropy law, under the restrictions connected with the finiteness of the resources available to the system.
The suggested way of describing natural systems is certainly insufficient for building a theory and presents just certain foundations of a potential programme of studies. Such a programme should, in particular, provide the consistent possibility of obtaining the traditional dynamic equations in specific fields where these equations are already known, in other words, it should provide the fulfilment of the correspondence principle. A derivation of equations can be thought of as a conseqence of the maximum entropy principle, unlike I.Prigogine's (1985) programme of studies where the dynamic equations were considered to be initially given and the point was to supplement them with the ways of introducing the entropy (as a Liapunov function of the dynamic equations) and with allowed state selection principles on the basis of the second law of thermodynamics.
3. The hypothesis of generating flows
3.1. The nature of the time flow
Having learnt to parametrize time by substitutional or entropy clocks, are we able to say something about the very origin of variability, or, in other words, about the nature of the time flow, or about the origin of the general process?
In the framework of the weak hypothesis (see Section 1.3), i.e., dealing with the over-molecular levels of, say, the biological hierarchy (molecules, cells, organisms, populations, communities, the biosphere), we can answer the question of origin: the energy and substrate flows in the biosphere of the Earth are created by the initial flow of solar photons which causes and creates all the other flows in the biological hierarchy.
Such a viewpoint is generalized by the strong hypothesis. Not only every motion has a metabolic nature (a motion of an object in a medium is absorption and emission of the elements of that medium; the space is a medium made of pre-elements), but, in addition, the very origin of element replacements is due to an external flow piercing through the objects of the natural hierarchy. In other words, if an analogy between the biosphere and the Universe as systems is appropriate (the Universe is here to be understood as the domain available to instrumental study), then the time of the Universe is created by a certain flow of pre-elements of rather deep levels of the physical hierarchy, i.e., the Universe is unisolated, open, non-equilibrium and, moreover, it is the absence of equilibrium that creates the time flow in it.
Such an assertion is nearly evident for biological hierarchies, interpretable for geological and geophysical universums but seems quite unacceptable for physical objects. It is quite easy to imagine equilibrium systems for which the physical time flow is evident: free motion of a body, oscillations of a pendulum, motion of noninteracting bodies in a closed and isolated system (e.g., planets around the Sun). However, here one can also find a flow and to discover it, it is sufficient to just change the language describing the mechanical motion. Let us imagine displacements of bodies as absorption of some points of the space and emission of others. Formally such a description can be formulated quite similarly to that using geometric trajectories.
The associations connected with the idea of a creating flow, are not new in philosophy and natural science. One could mention the world picture in daosism, the modern physical vacuum, and J.Whitrow's quasi-substantial view concerning "a hypothesis ... by which there is a unique basic rhythm of the Universe" (1964, p.63). One could also mention Newton's absolute time flow (though, Newton's flow is entirely matter-independent (Newton 1687), while a generating flow is to be directly coupled to material objects). There is also N.A.Kozyrev's (1982) time flow which forms causality in the world, provides one of stellar energy sources and causes a new "meta-interaction" of the world objects (Yeganova 1984). I.A.Yeganova's paper mentioned a number of experiments whose results apparently require inclusion of N.A.Kozyrev's ideas (see also a succession of recent experimental works carried out by M.M.Lavrentyev with co-authors, 1990, 1991, 1992). The second volume of this book is dedicated to reviews and developments of N.A.Kozyrev's ideas.
Identification of the time flow with the existence of a substantial flow often meets the objection that the very notion of a flow already includes a tentative notion of time: one usually calls a flow a change of matter or field concentrations in the context of physical time. However, a more general understanding of a flow is possible. This understanding is fixed within the substitutional construction of time: entry of elements into a certain standard system is considered as element flow in the system, the entering acts are called the instants of time, the number of entries determines a measure of the "flow time". In other words, element number changes in a standard system are parametrized not by some external process (not by "physical time") but by the process of element substitution in the same system. For the generating flow a standard system is the Universe, open to entries of pre-elements of a certain deep levels of matter structure. Changes in the number of those pre-elements, i.e., the pre-element flows, determine the time of the Universe.
Having appeared as a logical extrapolation of the properties of metabolic time, the generating flow gives an opportunity to seek constructive approaches to the problems of natural science. A connection between the time flow and absence of equilibrium, between stream dissipation and irreversibility is trivial: the absence of equilibrium in a system, i.e., the existence of a substantial stream across it, is just the flow of time. What is non-trivial is the fact that a generating flow should exist for that triviality. The question of the "nature" of time and the "reasons" of its course, of the mechanisms of its formation, is transferred by the substantial flow hypothesis to the question of the origin and status of the substrate and energy "feeding" of our Universe.
In the construction of time the generating flow is a fundamental, primary standard object for the ordering principle (see Section 1.4), in other words, it creates the sequence of time instants. Time turns out to be linearly ordered because the generating flow has these specific properties. The irreversibility of time is not its inherent property but is inserted into the Universe along with the directional character of the pre-particle stream: the irreversibility of time exists as long as the generating flow has not been reversed.
The generating flow hypothesis is very radical and can influence many fields of natural science. A reader of restrained views can be offered to consider the flow hypothesis as just a convenient means for describing such phenomena as formation, development and the course of time, i.e., to transfer the flow concept from the field of ontology to the methods of gnoseology. However, a constructive set up of the problem is apparently not the question of whether the generating flow exists or not but the question of how to reveal it operationally, i.e., how to measure in a reproducible way some properties of the generating flow, distinct from its basic manifestation - the flow of time.
3.2. Elements of the picture of the world
A reformulation of the properties and problems of time in the language of the generating flow (whose properties are to be postulated in the same way as the primary properties of time) can be useful at any rate at least in two respects. First, new heuristics can be discovered. Second, the set of primary entities is reduced, therefore the picture of the world is simplified. The generating flow hypothesis is sufficient for constructing time, space, particles and interaction.... I would like to demonstrate some heuristics, reminding the reader that these are not rigorous results but rather just a programme of studies in the path of the metabolic approach.
Let us identify the sources of generating flow entry to the universe (or flow discharge from it) with the charged particles. Existence of several generating flows can be admitted, so that the Universe is open to pre-element flows of several deep levels of its structure. Particle charges are dynamic characteristics of the flows whose sources are the particles themselves. Various sorts of charges are created by generating flows of different hierarchy levels.
A superposition of the deep-level elements of the natural hierarchies forms the space (synonyms: a medium for particles, a substantial ether, a physical vacuum). Metabolic motion of objects in the space (ether) is accomplished not by "moving aside" of ether elements but as these elements penetrate the objects and replace the elements formerly situated in the objects. Thus there is no "ether friction" or "ether wind". A pictorial image of object structure would consist of "fountains" or "springs" spouting in a pond rather than eddies or tores. Sequences of pre-elements "emitted" by the particles form systems of neighbourhoods of the particles and create the notion of "proximity" in space, i.e., the construction of its topology.
The assumption that the particles of matter are "entrances" and "exits" of the generating flows in our Universe, suggests the Lesage mechanism (Rosenberg 1935) for particle interaction: "The modern proof of the Newton theorem rests upon the hydrodynamic considerations dating back to Laplace: the point is that the only spherically symmetric motion of an incompressible fluid is radial motion with velocities inversely proportional to squared distances from the center... Thus the attracting force field of a point mass mathematically coincides with the field of velocities of an incompressible fluid" (Arnold 1987). Pre-element emission and absorption can be treated as pre-element exchange between particles, in correspondence with the construction of interaction traditional for theoretical physics. Different generating flows thus correspond to both different sorts of charges and different types of interactions.
Depending on which of the generating flows is chosen as a standard for measuring time (different generating flows can turn out to be non-uniform with respect to each other), the corresponding interaction can be eliminated from the description of motion. For instance, for the perfect physical time of the laws of mechanics the role of the imperativity postulate is played by the axiom of inertia claiming that those time intervals are equal, during which a body covers equal distances in the absence of interaction with other bodies. Thus the uniformity of the time scale is connected with the absence or presence of object interactions. Any nonlinear transformation of the temporal variable in the equations of mechanics leads to the appearance of terms responsible for additional interactions (Misner et al. 1977). Thus interaction can be described in terms of nonlinear time scales.
In general relativity a similar viewpoint is logically completed: instead of the world picture including interactions in flat space-time, it is suggested to consider a world possessing curvature (the latter is not reduced to time), with no necessity of the concept of (gravitational) interaction. E.Milne (1948) achieved a similar result, i.e., elimination of interaction, due to coordinate transformations, operating only with a nonlinear modification of the time scale.
Non-uniformity of the time scale can be treated as inhomogeneity of time, implying, by Noether's theorem, energy nonconservation. For the metabolic construction of time such a nonconservation is not "criminal" since the metabolic time flow emerges only in systems open to an external pre-particle flow, so that the question of uniformity or homogeneity of that flow is reduced to a reference level where time has been defined. If the standard is chosen so that the flow is uniform, then in the corresponding equations of motion there will be no interaction and the energy will be conserved. If the choice implies a non-uniform flow, then the equations will contain forces and energy nonconservation will be "legalized".
The substitutional approach enables one to try to introduce a construction of causality. Let us consider a situation where a pre-element of the generating flow is emitted by a source particle and absorbed by some other object. Let us call such a process a causal link, the event of emission of a fixed pre-element - the cause in the causal link and the event of absorption of the same pre-element - the consequence. If the "generating flow propagation velocity" is finite (according to the interpretations of Section 1.3), it corresponds to a certain average number of pre-elements in elements. The cause and the consequence turn out to be separated by a space-time interval. A more detailed discussion of the relations between the "time flow" and the ideas of causality is contained in the second volume of this book, dedicated to N.A.Kozyrev's ideas.
The generating flow propagation with respect to particles-sources can have different signs depending on whether emission or absorption occurred. A preferential flow direction, apart from the course of time, inequivalence of the right and left-handed coordinate frames and also different signs of charges. A gedanken operation of flow "reversal" should lead to the three connected effects: to time reversal ("temporal parity" nonconservation), to interchanging of left and right-handed coordinate frames ("spatial parity" nonconservation) and to changed signs of particle charges ("charge parity" changing; an antiparticle, as it is adopted in quantum electrodynamics, turns out to be a particle moving "against time"). A generating flow reversal (and the corresponding combined changes of the charge, spatial and temporal parities) apparently does not change the state of the world.
While the physical processes take place in a medium of pre-elements, which are not particles and whose emission creates the particles possessing mass and other charges, the overmolecular hierarchies, in particular, those connected with life, are determined by media constructed of particles themselves.
The general process, underlying the metabolic construction of time, has a number of properties which stress its similarity to the process called life and considered as a complex of connected changes: matter exchange, growth, development, reproduction, evolutionary changes.... The general process is a concept of less unidirectional nature (concerning the processes of life) than that of, e.g. E.Bauer's (1935) "stable non-equilibrium", at least because it also includes such processes as degradation and destruction. Nevertheless, attempts to understand the properties of biological time can turn out to be the same as a description of the essence of life. V.P.Voitenko (1985, p.74) cames to a similar conclusion: "the connection of the time measurement "technology" with such fundamental processes as cell growth and fission or matter exchange point out that the biological clock is not an annex of the biosystem building but the building itself". P.B.Gofman-Kadoshnikov (1984) also paid attention to the similarity between life and the general process; he stressed that self-renovation by element replacement is the basic system property of life which distinguishes biological systems from physical and chemical ones. In G.E.Mikhailovsky's opinion (1989, see also a chapter in this book), it is just the temporal organization of biological systems that determines the qualitative peculiarity of life. V.I.Vernadsky (1967, p.65) also wished to stress the identity of the two processes which are of interest to us; he mentioned the following words belonging to the classic: "Life is a more or less rapid, more or less complicated vortex whose direction is always the same and which always captures the molecules possessing certain properties; however, individual molecules continuously penetrate it and leave it, so that the shape of a living body is more significant for it than matter. As long as this motion exists, the body where it takes place, is alive.... When the motion finally stops, the body dies" (Cuvier 1817).
The generating flow hypothesis admits more radical assumptions concerning the specific nature of life than the analogies with metabolic motion. As well as the particles-charges are sources of generating flows which create physical interactions, the living organisms are sources of specific pre-element flows of some matter structure hierarchy levels (Levich 1993). Different flows may be responsible for the properties of life, consciousness, passionarity (on passionarity see L.N.Gumiliov 1989). The properties of life by their origin become similar to those of, e.g., electric and baryonic charges. The difference between life and unanimate matter turns out to be connected with the specific nature and quantities of the generating flows existing in the phenomenon of time.
An experienced reader can suspect in those hypothetic substantial flows of the metabolic approach a revival of the "vital forces" of vitalism, for instance, Aristoteles' entelechia, Wolf's vis essentialis or Blumenbach's nesus (Drisch 1915). However, the assertions of the metabolic construction are much more prosaic: we are dealing with material, although undetected by modern scientific instruments, structure levels of natural systems. The hypothetic pre-element flows of those pre-elements are required not in order to introduce some kind of vital forces but are in accord with the derivation logic of the metabolic approach leading to a whole circle of constructions related to the time phenomenon in natural sciences.
3.3. Getting rid of the bugaboo of thermal death
If one recognizes the generating flows, he thus removes the opposition between the second law of thermodynamics and the existence of development since the second law is valid only for isolated systems. The applicability of the second law to the open part of the Universe, where the generating flows create the course of time, is also avoided; however, this conclusion does not make a discovery for both physicists and astronomers: "...the everyday experience convinces us that the properties of nature have nothing in common with those of an equilibrium system, while the astronomical data show that the same is valid for the whole enormous part of the Universe available to our observations" (Landau and Lifshitz 1964, pp. 45-46). Moreover, "separate celestial bodies and their systems are so well isolated from each other that thermal death must noticeably approach them before any external system could interfere. Therefore degraded states of systems ought to be predominating, whereas in practice they are nearly never observed. Thus the problem is not only to explain why the Universe as a whole is far from equilibrium, it has a much more concrete meaning: to gain an understanding why separate systems and even separate bodies continue to live despite their short relaxation times" (Kozyrev 1963, p.96).
The theory which based on the maximum entropy principle (see Section 2) does not return to the second law of thermodynamics since it is applied to a system open to substrate and energy. Moreover, the entropy formula has been obtained apart from any probabilistic prerequisites, therefore the interpretation of the extremum principle as that requiring to pass from a less probable state to a more probable one, disappears. The restriction of system development by available substrate and energy flows in solving the variational problem (2.4) do not lead to a homogeneous distribution. On the contrary, extremely non-uniform distributions of system characteristics appear, like that of Gibbs (formula (2.5) in Section 2.4); in addition, opportunities of structure formation, i.e., selforganization, are implied.
The interpretations of the extremum principle from Section 2.3 in the language of generating flows can be supplemented by such formulations as ![]() "generating substance" economy and
"generating substance" economy and ![]() increased complexity in the process of natural evolution of open, unisolated systems, or increased self-organization.
increased complexity in the process of natural evolution of open, unisolated systems, or increased self-organization.
The entropy extremum principle applied to the Universe open to generating flows, drastically changes the view of world evolution. Here is the future of the Universe drawn by I.D.Novikov: "... If there are no appreciable amounts of matter, unobserved by some reasons, between the galaxies, then the Universe will expand forever.... In about hundred thousand billion years the very last stars will die out.... Despite the present-day absence of direct experimental data, the totality of our physical knowledge indicates that the matter of the Universe is unstable and, although very slowly, decays.... Black holes, the remaining after the death of some massive stars and also existing in the galactic cores, also evaporate due to quantum processes.
Thus both the cooled stars and the dilute gas, and later the black holes, will disappear from the Universe in its remote future... and only rare electrons and positrons, spread over huge distances from each other, will remain".
The future of the world is described still more dramatically according to "the Helvetius principle" (The time whose tooth chews up iron and pyramids, sees only the death which it brings" - Helvetius 1974, p.114) by Yu.B.Molchanov (1990, p.133): "...everything disappears in time, and disappears tracelessly, and that's the true essence of time".
The generating flow hypothesis gives an opportunity to put forward, in contrast to the Helvetius principle, another one, worth calling "the Kozyrev principle" ("Evidently some possibilities of struggle against the thermal death must be contained in the most basic properties of matter, space and time, there must be processes opposite in direction, those which can be called the processes of life. Those are the processes which keep the eternal life of the Universe." - Kozyrev 1963, p.96): as long as the Universe is open to generating flows, its evolution is accompanied by self-organization, increasing inhomogeneity and complexity.
REFERENCES
ABAKUMOV V.A. (1969). The duration and frequency of generations. Trudy VNIRO. V.67. Pp.344-356 (in Russian).
ALEXEYEV V.P. (1975). The vector of time in the taxonomic continuum. Voprosy Antropologii (The Problems of Anthropology). 49th issue. Pp.65-77 (in Russian).
ARISTOTELES (1981). V.3. Physics. Moscow (in Russian).
ARNOLD V.I. (1987). Three hundred years of mathematical natural science and celestial mechanics. Priroda (Nature). N.8. Pp.5-15.
BACKMAN G. (1943). Wachstum und Organische Zeit. Leipzig.
BAUER E.S. (1935). Theoretical Biology. Moscow (in Russian).
BOURBAKI N. (1939). Éléments d'histoire des mathématiques. Paris.
CHEBURAYEVA A.N. (1977). Periodic coenopopulation dynamics of Shell's in northern meadow steppes. In: Plant Coenopopulations: Development and Interrelations. Pp.50-57. Moscow (in Russian).
CUVIER G. (1817). La régne animal distribué d'après son organisation. 1. Paris. Pp.12-13.
DETTLAFF T.A. and DETTLAFF A.A. (1982). Dimensionless criteria as a method of quantitative characterization of the development of animals. In: Mathematical Biology of the Development. Pp.25-39. Moscow (in Russian).
DMITRIEV V.Yu. (1978). Some problems in the studies of the systematic variety of fossil organisms. Paleontologichesky Z. (J. Paleontol.). N.2. Pp.122-132 (in Russian).
DRIESCH H. (1922). Gerschichte des Vitalismus. Lpz.
FLEISCHMANN B.S. (1986). The temporal-biological "logarithm law" as a consequence of the general system-theoretical hyperbolic law of regenerating system reliability. In: Temporal Aspects of Modelling and Forecasting in Ecology. Riga. Pp.85-97 (in Russian).
FRENKEL A. and BAR-HILLEL I. (1958). Foundations of Set Theory. Amsterdam.
FRIEDMANN A.A. (1965). The World as Space and Time. Moscow (in Russian).
GAVRILOV G.P., STOLIAROV A.Yu. and LEVICH A.P. (1986). The adequacy of alternative models in ecology of communities. In: Ecolological Forecasting. Moscow (in Russian).
GOFMAN-KADOSHNIKOV P.B. (1984). A system analysis of the hierarchy of levels of life. In: Sistemnye issledovaniya (System Studies). Moscow (in Russian).
GOODWIN B. (1963). Temporal Organization in Cells. A Dynamic Theory of Cellular Control Processes. London and New York.
GUMILIOV L.N. (1989) Ethnogenesis and the Biosphere of the Earth. Leningrad (in Russian).
HELVÉTIUS (1907) Notes de la main. Paris.
HOFECKER G., SKALICKY M., KMENT A. and NIEDERMULLER M. (1981). Math-ematical models of the biological age of the rat. Adv. Physiol. Sci. V.34. Pp.47-52.
KOZYREV N.A. (1963). Causal mechanics and the possibility of experimental studies of the properties of time. In: History and Methodology of Natural Science. 2nd issue. Moscow (in Russian).
KOZYREV N.A. (1982). Time as a physical phenomenon. In: Modelling and Forecasting in Bioecology. Riga. Pp.59-72 (in Russian).
LAVRENTYEV M.M., YEGANOVA I.A., LUTSET M.K. and FOMINYKH S.F. (1990). On a distant influence of stars upon a resistor. Dokl. AN. V.314. N.2. Pp.352-355 (in Russian).
LAVRENTYEV M.M., GUSEV V.A., YEGANOVA I.A., LUTSET M.K. and FOMINYKH S.F. (1990). On a detection of the true position of the Sun. Dokl. AN. V.315. N.2. Pp.368-370 (in Russian).
LAVRENTYEV M.M., YEGANOVA I.A., LUTSET M.K. and FOMINYKH S.F. (1991). On a detection of a response of matter to an external irreversible process. Dokl. AN. V.317. N.3. Pp.635-639 (in Russian).
LAVRENTYEV M.M., YEGANOVA I.A., MEDVEDEV V.G., OLEINIK V.K. and FOMINYKH S.F. (1992). On scanning the starlit sky by a Kozyrev probe. Dokl. AN. V.323. N.4. Pp.649-652 (in Russian).
LANDAU L.D. and LIFSHITZ E.M. (1964). Statistical Physics. Moscow (in Russian).
LEVICH A.P. (1978). Information as system structure. Semiotika i informatika. N.10. Pp.116-132 (in Russian).
LEVICH A.P. (1980). The Structure of Ecological Communities. Moscow (in Russian).
LEVICH A.P. (1982). Sets Theory, the Language of Category Theory and Their Applications in Theoretical Biology. Moscow (in Russian).
LEVICH A.P. (1993a). Theoretical biology: a search of equations of generalized motion and the sources of the non-equilibrium state of living matter. Biology Bulletin of the Russian Academy of Sciences. V.20. N.2, 5. Pp.266-269.
LEVICH A.P. (1993b). Toward a dynamic theory. In: Lectures in Theoretical Biology. Pp.33-50. V.2. Tallinn.
LEVICH A.P., REVKOVA N.V. and BULGAKOV N.G. (1986a). The "consumption-growth" process in microalgae cultures and the mineral component nutrition requirements of cells. In: Ecological Forecasting. Pp.132-139. Moscow (in Russian).
LEVICH A.P., LIUBIMOVA E.D. and MARTASHVILI G.Sh. (1986b). Species structure and the consumption of substrate and energy factors in laboratory algocoenoses. In: Ecological Forecasting. Pp.69-103. Moscow (in Russian).
LEVICH A.P., ZAMOLODCHIKOV D.G. and RYBAKOVA S.Yu. (1993a). A study of the adequacy of a category-theoretic model of phytoplankton communities. In: Ecological Monitoring and Modelling Problems in Ecology. V.15. Pp.234-246. St.Petersburg (in Russian).
LEVICH A.P., ALEXEYEV V.L. and RYBAKOVA S.Yu. (1993b). Optimization of the structure of ecological communities: a model analysis. Biophysics. V.38. N.5. Pp.903-911.
LEVICH A.P., ALEXEYEV V.L. and NIKULIN V.A. (1994). Mathematical aspects of variational modelling in ecology of communities. Matematicheskoye modelirovaniye. V.6. N.5. Pp.55-71. (in Russian).
LURIE D., VALLS J. and WAGENSBERG J. (1983). Thermodynamic approach to biomass distribution in ecological systems. Bull. Math. Biol. V.45. N.5. Pp.869-872.
MARTYNOV D.Ya. (1961). Ages and Instants. Moscow (in Russian).
MCCAY C.M., CROWELL M.F. and MAYNARD L.A. (1935). The effect of retarded growth upon ultimate body size. J. Nutr. V.10. Pp.62-79.
MILNE E.A. (1948). Kinematic Relativity. Oxford.
MISNER C., THORNE K. and WHEELER J. (1973). Gravitation. San Francisco.
MIKHAILOV I.I. (1985). Physico-geographic Regioning. Moscow (in Russian).
MIKHAILOVSKY G.E. (1988). Description and Estimation of the State of Plankton Communities. Moscow (in Russian).
MIKHAILOVSKY G.E. (1989). Organization of time in biological systems. Z. Obshchey Biol. (J. General Biol.). V.50. N.1. Pp.72-81 (in Russian).
MIKHAILOVSKY G.E. (1982). The concept of entropy applied to self-reproducing biological systems. In: Man and Biosphere. 6th issue. Pp.62-78. Moscow (in Russian).
MOISEYEVA N.I. (1980). Properties of biological time. In: The Factor of Time in the Functional Organization of Living Systems. Pp.15-20. Leningrad (in Russian).
MOLCHANOV Yu.V. (1990). The Problem of Time in Modern Science. Moscow (in Russian).
NEWTON I.S. (1687). Philosophiae Naturalis Principia Mathematica. London.
NOÜY L.P. (1936). Biological Time. London.
NOVIKOV I.D. (1990). Where Does the River of Time Flow? Moscow (in Russian).
PRIGOGINE I. (1980). From Being to Becoming: Time and Complexity in the Physical Sciences. San Francisco.
ROBINSON A. (1966). Non-standard Analysis. Amsterdam.
ROSENBERG F. (1935). History of Physics. Part 3. 1st issue. Moscow-Leningrad (in Russian).
SCHMIDT-NIELSON K. (1987). Animal Sizes: Why are They so Important? Moscow (in Russian).
SHAHER B.L. (1982). Ageing of Nesokia by weighing the eye lens. Pakistan J. Zool. V.114 (1). Pp.103-105.
SHAROV A.A. (1977). Information concepts in category theory. Semiotika i informatika. 8th issue. Pp.167-178. Moscow (in Russian).
SVIRIZHEV Yu.M. and PASEKOV V.P. (1982). Foundations of Mathematical Genetics. Moscow (in Russian).
THORNEWAITE C.W. (1953). Operations research in agriculture. J. Operations Res. Soc. Amer. N.1. Pp.33-38.
TOMSON W. and TAIT P.G. (1890). Natural Philosophy. Cambridge.
TOWARDS THEORETICAL BIOLOGY. V.1. Prolegomena. (1968). Ed. by C.H.Waddington. Birmingham.
URANOV A.A. (1975). The age spectrum of a phytocoenopopulation asa function of time and wave-energy processes. Nauchnye doklady vysshey shkoly. Biologicheskiye nauki. (Scientific Reports of Higher Education Institutions. Biological Sciences). N.2. Pp.7-34 (in Russian).
VASILYEV V.K., LUKYANOV N.K. and SAVVIN A. (1974). The concept of proper time of biological processes and its application to studies of gas exchange dynamics. Kosmicheskaya biologiya i aviacosmicheskaya meditsina (Space Biology, Aviation and Space Medicine). N.5. Pp. 12-17 (in Russian).
VERNADSKY V.I. (1957). Essays on geochemistry. Moscow (in Russian).
VERNADSKY V.I. (1988). Philosophical Thoughts of a Natural Scientists. Moscow (in Russian).
VINOGRADOV M.E. and SHUSHKINA E.A. (1983). Succession of sea plankton communities. Okeanologiya. V.23. 4th issue. Pp.633-639 (in Russian).
VOITENKO V.N. (1985). Time and clocks as a problem of theoretical biology. Voprosy filosofii (Problems of Philosophy). N.1. Pp.73-82 (in Russian).
WHITEHEAD A. and RUSSEL B. (1910-1913). Principia Mathematica. V.3. Cambridge.
WHITROW J. (1961). The Natural Philosophy of Time. London and Edinburgh.
YEGANOVA I.A. (1984). An Analytic Overview of the Ideas and Experiments of Modern Chronogeometry. VINITI depot N.6423-84 (in Russian).
ZOTIN A.I. and ALEXEYEVA T.A. (1984). The Rubner constant as a criterion of life duration for a species. Fiziologichesky Z. (J. Physiol.). V.30. N.1. Pp.59-64 (in Russian).