
Variational Modelling Theorems and Algocoenoses Functioning Principles
A.P. Levich
General Ecology Lab, Biological Faculty, Moscow State University, Moscow 119899, Russia

Abstract
Natural system structure modelling on the basis of category and functor theory makes it possible to formulate extremal principles of system modelling and to derive functionals for setting up variational problems in the ecology of communities.
Variational modelling allows one to predict and understand many features of stationary states of communities of many species that consume mutually irreplaceable resources.
A solution to the variational problem, that is, the species structure formula, allows one to calculate the abundance of a member species of a community as a function of the resources which restrict its development and the demands of individuals for these resources. It is possible as well to solve the inverse problem: given the population abundances and the amounts of limiting resources, estimate the demands. One can also calculate the partial consumption of any resource by each population, given its consumption by the whole community.
Analytical consequences of the variational modelling also suggest interpretations and analogues of the functional to be extremized: entropy, free energy, exergy, complexity, information, self-organization, expansion, degree of structuredness, degree of stability, diversity and the limiting resources consumption. The origin and the ecological meaning of the model constructs is discussed, including rank distributions, diversity indices and Lagrange multipliers.
The adequate consequences of variational modelling have been verified by numerous experimental data on laboratory and natural (in vitro and in situ) algocoenoses.
Keywords: Variational modelling; Extremal principles; Limiting rules; Biogenic manipulation in algocoenoses.
1. Introduction
A conventional way of formal modelling of system dynamics is to employ differential equations. These equations are either guessed or obtained phenomenologically, by formalizing empirical laws and using plausible reasoning. There is also an approach which postulates, instead of equations, a variational principle and the form of a functional to be extremized. The equations themselves then follow from solving the appropriate variational problem. Such an approach is used both in the problems of theoretical ecology (e.g. Lotka, 1922; Margalef, 1958; McArthur, 1969, 1970; Odum, 1971; Samuelson, 1974; Insarov, 1975; Cohen, 1979; Schmelzer et al., 1981: Semevsky and Semenov, 1982; Lurie et al., 1983; Straš kraba and Gnauck, 1985; JØ rgensen, 1986, 1988, 1995; Mauersberger and Straš kraba, 1987; Svirezhev, 1991; Zeide, 1991; Nielsen, 1995; 1997; Patten, 1995; Washida, 1995; Webb, 1995; Bendoricchio and JØ rgensen, 1997) and in solving a wide range of general biological problems. One of the unsolved problems is to deepen the traditional approach, namely, to try to find arguments making it possible to derive rather than guess the functionals able to form a basis for variational modelling in ecology.
It is well-known that, for example, in theoretical physics the functionals are frequently guessed with the aid of such considerations as their invariance with respect to the transformations admitted by the physical principles. It is suggested to look for such arguments applicable to biological systems of many organisms.
The purpose of the present publication is to bring to the readers' judgement the up-to-date theoretical and applied results of variational modelling in the ecology of communities. It is proposed to judge about the extent to which the ideas have been realized by the adequacy of the resulting variational model and by the predictive ability of its analytical consequences when applied to the description of important ecological principles.
2. The experimental context of the studies
The ecological applications of the model have been investigated for groups of organisms which need several mutually non-interchangeable resources. These can be, for instance, communities of autotrophic organisms consuming carbon, nitrogen, phosphorus, silicon, energy of light, etc., or communities of bacteria growing on several substrates which are simultaneously necessary for them. The point under study is the existence of communities of several species of organisms competing for common resources.
The model describes the growth of organisms under the condition of a nonrenewable resource deposit. In vitro, this situation corresponds to batch cultivation rather than continuous one. I would note that the continuous cultivation, unlike the batch one, not only renews the nutrient deposits in the environment, but also eliminates biomass of all the species of the community in the same proportion, depending on the flow velocity. This circumstance manifests an essential difference between the continuous cultivation and the processes that take place in natural conditions, where biomass elimination is always species-dependent. On the other hand, the batch cultivation may serve as a prototype for some natural systems, such as reservoirs whose nutrient deposits are refilled once or twice a year, when the enriched waters from under the thermocline are mixed with the water masses of the photic layer (Odum, 1983).
The period under study is that between inoculation and growth termination, when the latter is caused by exhausting one of the resources rather than some other reason (such as auto-toxication, allelopathic interactions, etc.).
It is taken into account that the growth of organisms is determined not only by the resource deposits in the environment, but also their intracellular deposits. Namely, one of the physiological mechanisms of the effect of the deposits upon the growth is meant: cellular fission terminates when the intracellular deposit of one of the mutually irreplaceable resources reaches a certain species-dependent minimal value (Droop, 1973). A special experimental development is necessary for taking into account this circumstance (Levich and Artyukhova, 1991).
The model verification and the approbation of the resulting methods of community structure control were carried out using the data about laboratory and natural phytoplankton communities. The materials and methodologies, which served as a basis for obtaining these data, are presented in the sections of the paper where the corresponding experiments are mentioned, in order to rid the reader of returning to a previously read material.
3.Model description
I build a model of a community of organisms where groups differ from one another in physiological demands for resources (these may be populations of different species or other physiologically homogeneous groups of individuals). It is convenient to describe such a community in terms of a set of
n elements, split into w non-intersecting classes, with the number ni of elements in a class (Due to this circumstance, I use a consequence of the above local formulation of the extremal principle: the system proves to be in a state with the most extremal structure (within the limits admitted by the resources).
Consider a community of unicellular organisms, where death and fission of cells are admitted, but their fusion and introduction from outside are forbidden. In this case, a specific invariant of the partitioned sets structure is (Levich, 1995c)
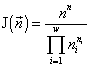 ,
,
where 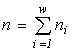 is the total abundance of the community. The logarithm of this invariant, called the generalized entropy (Levich, 1995c), is
is the total abundance of the community. The logarithm of this invariant, called the generalized entropy (Levich, 1995c), is
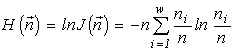
(a connection between the invariants and Boltzmann's expression for the entropy and the diversity indices is discussed in more detail in Section 4.4).
There appears a variational problem of finding a conditional extremum:
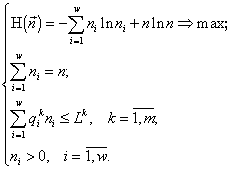 (1)
(1)
Here
n and ni are the final abundances to be found, Lk is the sum of the initial content of the resource k in the environment and in the cells (Lk4. Variational modelling theorems and their ecological consequences
4.1. Stratification Theorem
Formulation of the theorem
(Levich et al., 1994)The whole resource factor space  splits (stratifies) into
splits (stratifies) into ![]() non-intersecting domains (strata), each stratum corresponding to one of the subsets of the set of resources consumed by the community. For each stratum SJ, where J ¹
Æ
is a subset of the set of resources {1,2,...,m}, one has:
non-intersecting domains (strata), each stratum corresponding to one of the subsets of the set of resources consumed by the community. For each stratum SJ, where J ¹
Æ
is a subset of the set of resources {1,2,...,m}, one has:
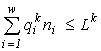
The theorem yields an algorithm for calculating the strata for a set of quotas ![]() specified in the community. Figs.1 and 2 present the stratification of the environmental factor space for m = 2 and m = 3. The Stratification Theorem implies a reduction of the problem (1) to the problems
specified in the community. Figs.1 and 2 present the stratification of the environmental factor space for m = 2 and m = 3. The Stratification Theorem implies a reduction of the problem (1) to the problems
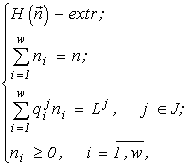 (2)
(2)
formulated for any J Ì {1,2,...,m}.
The Limiting Link Rule
The biological interpretation of the Stratification Theorem leads to the Limiting Link Rule for communities of many species, whose populations compete for several resources (Levich et al., 1993b). I will call limiting resources the resources which are entirely consumed by the community from the environment, i.e. those for which the balance inequalities from the problem (1) turn out to be equalities. According to the Stratification Theorem, from a specified set of resources ![]() , entirely consumed are (i.e. restrict the growth of the community) those resources which belong to the set J that identifies the stratum SJ, the specified vector
, entirely consumed are (i.e. restrict the growth of the community) those resources which belong to the set J that identifies the stratum SJ, the specified vector ![]() belongs to. Thus the Stratification Theorem makes it possible to rigorously predict the resources which limit the growth of a community with a specified set of quotas
belongs to. Thus the Stratification Theorem makes it possible to rigorously predict the resources which limit the growth of a community with a specified set of quotas ![]() .
.
For monocultures the Limiting Link Rule coincides with Liebig's minimum principle (Liebig, 1840), namely: for L1/L2 £ q1/q2 the factor 1 is limiting (Fig. 3). This condition is equivalent to L1/L2 < q1/q2, i.e., the limiting resource is the one for which the abundance reached on its deposit is minimal (i.e. the one which “is in its minimum” in the above sense). I would like to note that, formally, the problem (1) is not defined for w = 1, since in this case the functional becomes a constant. But the problem may be solved in this case just on the basis of the resource limitations which give
![]() ,
,
i.e., ![]() , or Liebig's minimum principle, is realized.
, or Liebig's minimum principle, is realized.
For communities of more than one species, according to the Limiting Link Rule, there are both domains where the growth is restricted by a single factor and those with several limiting factors, in particular, all the factors. The latter situation is called in the agronomical literature Mitscherlich's "Law of joint action of factors" (Mitscherlich, 1909). Experiments with phytoplankton (Droop, 1973; Rhee, 1978; Ahlgren, 1980; De Groot, 1983) demonstrate the predicted switching of the limitation.
The domains of the limitation when the community growth depends, for example, on two resources, L1 and L2, is calculated in the following way (Levich et al., 1993b). Let x0 be the unique root of the equation  , and y0 the unique root of the equation
, and y0 the unique root of the equation 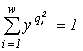 . Then the quantities
. Then the quantities  and
and 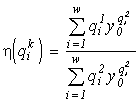 determine the boundaries of the domain
determine the boundaries of the domain ![]() , where the community growth is limited by both resources L1 and L2. When
, where the community growth is limited by both resources L1 and L2. When ![]() , the first factor is limiting, and when
, the first factor is limiting, and when ![]() , the second one. Table 1 gives an example of calculating the nature of limitation for an algocoenosis whose growth is potentially limited by nitrogen and phosphorus. Examples of calculations for other coenoses and for m > 2 are given in the paper cited above (Levich et al., 1993b).
, the second one. Table 1 gives an example of calculating the nature of limitation for an algocoenosis whose growth is potentially limited by nitrogen and phosphorus. Examples of calculations for other coenoses and for m > 2 are given in the paper cited above (Levich et al., 1993b).
I propose the description of a direct experiment for verifying the Limiting Link Rule. For an algocoenosis with known demands of the species, ![]() (
(![]() ), one puts
), one puts ![]() flasks with initial values
flasks with initial values ![]() of the set of consumable resources belonging to each stratum J. Once the growth has stopped, one pours out the content of each flask to
of the set of consumable resources belonging to each stratum J. Once the growth has stopped, one pours out the content of each flask to ![]() new flasks and adds to each of them one of the sets of resources J. The renewal of growth in a secondary flask with the addition of a minimal (by inclusion) set J indicates that just this set had been the limiting one in the corresponding primary flask. Such an experiment has been performed (Levich and Lichman, 1992) with a community of species of micro-organisms (the green algae Scenedesmus quadricauda (Turp.) Breb., Ankistrodesmus falcatus (Codra) Ralfs and the cyanobacteria Anabaena variabilis (Kutz), with different initial environmental concentrations of nitrogen and phosphorus. The quotas of the species,
new flasks and adds to each of them one of the sets of resources J. The renewal of growth in a secondary flask with the addition of a minimal (by inclusion) set J indicates that just this set had been the limiting one in the corresponding primary flask. Such an experiment has been performed (Levich and Lichman, 1992) with a community of species of micro-organisms (the green algae Scenedesmus quadricauda (Turp.) Breb., Ankistrodesmus falcatus (Codra) Ralfs and the cyanobacteria Anabaena variabilis (Kutz), with different initial environmental concentrations of nitrogen and phosphorus. The quotas of the species, ![]() and
and ![]() were determined in monocultures of the same species using a special methodology (Levich and Artyukhova, 1991). The results of the experiment coincided with the predicted sets of limiting factors (only nitrogen, only phosphorus or jointly nitrogen and phosphorus) for different initial values of the environmental concentrations.
were determined in monocultures of the same species using a special methodology (Levich and Artyukhova, 1991). The results of the experiment coincided with the predicted sets of limiting factors (only nitrogen, only phosphorus or jointly nitrogen and phosphorus) for different initial values of the environmental concentrations.
Selection of species for balanced utilization of multicomponent substrates
The species selection problem is solved by two stages (Zamolodchikov and Levich, 1992). One should first choose the quota matrix ![]() in such a way that the boundaries of the total consumption stratum embrace the specified vector of environmental resources (for instance, a cone with the boundaries
in such a way that the boundaries of the total consumption stratum embrace the specified vector of environmental resources (for instance, a cone with the boundaries ![]() and
and ![]() for m = 2 and the vector
for m = 2 and the vector ![]() in Fig. 1). At the second stage, given the quota matrix
in Fig. 1). At the second stage, given the quota matrix ![]() , one should choose real species with the necessary demands (quotas). Such a problem may be useful for biological decontamination of waters, for composing cultivation media, etc.
, one should choose real species with the necessary demands (quotas). Such a problem may be useful for biological decontamination of waters, for composing cultivation media, etc.
4.2. Solution of the variational problem
Species structure formula. Sufficient and necessary conditions of an extremum
The problems (2) have the solutions
![]() , (3)
, (3)
where the vectors ![]() ,
, ![]() and
and ![]() have components j from the set J which identifies the stratum containing the vector
have components j from the set J which identifies the stratum containing the vector ![]() . The Lagrange multipliers
. The Lagrange multipliers ![]() and the total abundance n are sought as functions of the resources
and the total abundance n are sought as functions of the resources ![]() that are entirely consumed in the stratum SJ, from the algebraic equations
that are entirely consumed in the stratum SJ, from the algebraic equations
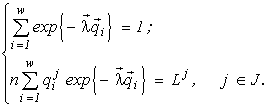 (4)
(4)
It has been shown (Levich et al., 1994) that a solution to (3) always exists, is unique and realizes a maximum of the functional ![]() . In applied ecology, the species structure formula (3) makes it possible to calculate quantitatively:
. In applied ecology, the species structure formula (3) makes it possible to calculate quantitatively:
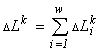 ;
;
Adequacy of the model
The species structure formula explains qualitatively the origin of rank distributions of the abundances ni of populations in communities. The origin of rank distributions is discussed in more detail in Section 5.1.
In an experiment with a polyculture of 10 species of green algae (Chlorella vulgaris (Bejerink.), Scotiella nivalis (Fritsch.), Chromochloris cinnoborina (Chodat.), Scenedesmus quadricauda (Turp.), Scenedesmus bijugatus (Lagerh.), Scenedesmus obliquus (Kruger.), Ankistrodesmus acicularis (Korschik.), Ankistrodesmus braunii (Brunnth.), Stichococcus mirabilis (Lagerh.) and Chlamydomonas humicola (Luksch.)) the abundances and biomasses of the species, the primary production and the concentrations of mineral forms of nitrogen and phosphorus were measured within 70 days in several repetitions. The demands of the cells for phosphorus was measured in monocultures of the same species. The algae grew in the storing regime, without bubbling, on Beneke's medium. The content of the nutrients in the medium was maintained in such a way that the algal development be limited by environmental phosphorus. At the stationary stage of the growth, the distribution of cells' abundances obeyed the species structure formula ![]() with a multiple correlation factor of 0.97 (Levich et al., 1986).
with a multiple correlation factor of 0.97 (Levich et al., 1986).
The same set of experiments, along with sixteen other ones, was, in addition, analyzed with the aid of the rank criteria of sample adequacy and cellular quota calibration (Zamolodchikov et al., 1993). The sets of experiments differed from each other in the choice of taxons (four to ten species in a polyculture) and in initial concentrations of nitrogen and phosphorus in the medium (Levich et al., 1997). When the growth is limited by a single resource, the place of a species in the decrease-ranged row of abundances at the stationary stage is entirely determined by the cellular quota rank of the species with respect to the limiting resource (the greatest abundance corresponds to the smallest quota). An attempt was made to pick out, within the experimental error, a unique set of cellular quota ranks measured in the experiment, in such a way as to reproduce the experimental abundance ranks in already all the sets of experiments where the growth was limited by a single resource. I succeeded to do so with Spearman's rank correlation factor of 0.92 to 1.00 (Table 2). For sets of experiments with more than one limiting factor, the adequacy of the species structure formula was verified in the following way. From the species' abundances measured in a pair of sets of experiments, the cellular quotas of nitrogen and phosphorus were calculated; then, using these calibrated quotas, the species' abundances were computed for all the other sets of experiments, and the results were compared with the experimental values. The comparison showed that the computed abundances coincide with the experimentally measured ones within the experimental errors.
Invariance of the species structure formula
The set of algebraic equations (4), after exclusion of the variable n, is written in the form
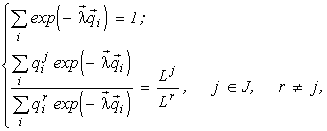 (5)
(5)
whence it follows that the Lagrange multipliers
lk and, simultaneously, the relative abundancesThe species' relative abundances ni/n are also invariant with respect to similarity transformations of the quotas ![]() (Levich et al., 1994), therefore the species structure formula allows one to calculate only ratios of quotas of different species with respect to each resource, but not their absolute values (this fact is also important for model calibration).
(Levich et al., 1994), therefore the species structure formula allows one to calculate only ratios of quotas of different species with respect to each resource, but not their absolute values (this fact is also important for model calibration).
The species structure formula makes it possible to find the resource dependence of the total abundance of the community and its entropy diversity index (Levich et al., 1994):

where ½
J½
is the number of limiting resources corresponding to the stratum SJ; 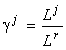 are the resource ratios, f and g are some functions.
are the resource ratios, f and g are some functions.
Examples of the species structure formula (justifications of the calculations are contained in the papers: Levich, 1980; Levich et al., 1994)
3) m = 2; w = 4. I will present the experimental values of nitrogen and phosphorus quotas for one of the sets of experiments with laboratory algocoenoses (dimension: 10-9 mg/cell):

The results of numerical calculations according to the species structure formula are presented in Fig. 5.
![]()
The results of the calculations are demonstrated in Fig. 7.
4.3. Theorem of Maximum Species Abundances
Analytical result
As has been indicated above, the set of equations (5) implies that the relative abundances of the species depend only on the ratios of the environmental resources which limit the growth. It has been proved (Levich et al., 1993a; Alexeyev and Levich, 1997) that the relative abundance of a species takes its greatest possible value if the environmental resource ratios coincide with the ratios of the species' demands for the same resources. Fig. 8 illustrates this result by a numerical calculation for the case m = 2, w = 4 and the experimental values of the quotas.
Phenomenological verification of the theorem
There is a number of well-established phenomenological dependences that reflect the empirical concepts of phytoplankton growth and consumption. They include, in particular, the Monod law (Monod, 1942) for resource absorption from the environment: ![]() , Droop's law (Droop, 1973) for the dependence of the growth rate on the intracellular concentrations of substances:
, Droop's law (Droop, 1973) for the dependence of the growth rate on the intracellular concentrations of substances: ![]() , the matter conservation law, etc. These dependences gave rise to the creation of simulative models taking into account the empirical generalizations. Since such models incorporate realistic data descriptions, these model should, like “big approximation formulae”, implicitly describe the “correct” behaviour of the communities. On the basis of these premises, I have tested the hypothesis of the controlling effect of the growth-limiting resources using the following simulative model (JØ
rgensen, 1980):
, the matter conservation law, etc. These dependences gave rise to the creation of simulative models taking into account the empirical generalizations. Since such models incorporate realistic data descriptions, these model should, like “big approximation formulae”, implicitly describe the “correct” behaviour of the communities. On the basis of these premises, I have tested the hypothesis of the controlling effect of the growth-limiting resources using the following simulative model (JØ
rgensen, 1980):

for w = 3 and 4; m = 2 (Levich and Lichman, 1992). In addition to the previously introduced notations, here: bi is the biomass of the i-th species; Vmax and umax are the greatest growth and absorption rates, respectively, and ![]() is the corresponding semi-saturation constant.
is the corresponding semi-saturation constant.
After model calibration based on experimental data for a laboratory algocoenosis, three computer experiments were conducted with, respectively, 45, 240 and 17 combinations of initial nitrogen and phosphorus concentrations. The dependence of the species abundances on the N/P ratio was not pre-loaded in the model. The results of the simulations confirm the hypothesis on the dependence of the relative abundances on the N/P ratio and on the proximity of the optimal N/P ratio to the ratio of the corresponding calibrated minimal quotas for each species.
Table 3 demonstrates, as ratio of species in 4-species polyculture varies depending on the resources ratio in a medium in the beginning of each computer experiment. At the lowest N/P Scenedesmus quadricauda cells contribute about 80 % to total biomass of polyculture, but biomass of, for example, Ankistrodesmus falcatus makes only 6-8%. At the increase of N/P species predominance in polyculture changes into opposite. Listed in Table 3 intervals of N/P values and species shares in polyculture are integrated on a few computer experiments. For example, in experiments with the N/P ratios in the beginning of experiment varying from 0.07 up to 5 share of S. quadricauda varied from 75 up to 80 %, and share S. obliquus varied from 3 up to 6 % and so on. Figure 9 shows similar change of subdominants in 3-specific polyculture (points marked on the graphs are the results of concrete computer experiments).
Experimental control of the composition of an algocoenosis with the aid of the environment resource ratio
The experiments of my colleagues and mine have been conducted with laboratory polycultures and with natural phytoplankton communities in vitro and in situ.
The numerous sets of laboratory experiments (Levich et al., 1997; Bulgakov and Levich, 1999) differed from each other in the algocoenosis compositions and in the initial nutrient concentrations in the medium. In the repeated experiments, one measured the abundances, cellular volumes and environmental resource concentrations both in the polycultures and in the corresponding monocultures. The initial intracellular deposits of the limiting resources were controlled, as well as such non-limiting parameters as light, temperature, acidity, micro-elements; algological and bacteriological purity, absence of metabolic interaction. The resource consumption by the whole community and the cellular demands were calculated. The experiments in the storing cultivation regime continued until a stationary stage of growth was reached. Fig. 10 presents the results of two experiments with two-species polycultures (Levich and Bulgakov, 1993). It should be noted that neither of these experiments contradicted the consequences of variational modelling.
Two experiments have been conducted with pond phytoplankton in different seasons (Levich et al., 1992; Bulgakov and Levich, 1999). The pond community contained more than a hundred of species belonging to several large taxons: Chlorophyta (Chlorococcales, Chlamydomonadales, Desmidiales), Bacillariophyta, Cyanophyta. In one of the sets of experiments (20-liter aquaria), three different N/P ratios, in the interval of 5 to 16, were tested; in another set (two-liter flasks) — five ratios in the interval of 2 to 200. The experiments were repeated several times. Fig. 11 illustrates the main trend: for Protococcales algae, high values of the N/P ratio are optimal, while for blue-green ones and diatomes — low ones (of course, these are not high taxons that respond to the N/P ratio, but the dominant species: among Chlorococcales these are S. quadricauda, among Cyanophyta these are the species of the genus Microcystis, among Bacillariophyta these are Nitzschia sp.). I can note that the qN/qP ratio for S. quadricauda is measured in tens of units (Levich and Artyukhova, 1991), while for the species of the genus Microcystis the optimal ratio is 5 to 10 (Rhee and Gotham, 1980). In the experiment being described, the effect of the N/P ratio on the size structure of the community was estimated as well. It turned out (Fig. 12) that, as N/P grows, the biomass of the class of small cells increases, while that of the large cells decreases (it is naturally not the cell size that is changing, but the proportion of the species with the corresponding cell size in the whole community).
The investigations in situ were conducted (Levich and Bulgakov, 1992; Levich et al., 1996 a,b; Bulgakov and Levich, 1999) for three years in seven experimental fish-breeding ponds of 0.25 to 3.5 hectares, about 1.5 m deep. Mineral nitrogen and phosphorus were delivered to the test and control ponds from the beginning of April in different proportions: N/P = 4 in control ponds and N/P = 25 to 30 in test ponds. Besides, the data about the phytoplankton and hydrochemical characteristics of the same ponds in other seasons were taken into account (about 20 “year-ponds” altogether). The biomasses of the phytoplankton populations were investigated, and the biochemical parameters of the ponds were controlled. High N/P ratios led to an increasing fraction of Protococcales algae and to a decreasing fraction of the blue-greens (whose composition was dominated by nitrogen-non-fixing species). Fig. 13 illustrates a typical dynamics of relative biomasses for one of the ponds in one of the seasons.
Numerous laboratory experiments with flow-type cultivation of strains and natural phytoplankton have revealed the existence of optimal species-dependent concentration ratios of nitrogen, phosphorus and silicon (Holm and Armstrong, 1981; Tilman, 1982; Sommer, 1983; Kilham, 1986; Suttle and Harrisson, 1988; Grover, 1989; De Pauw and Naessens-Foucquaert, 1991; Suttle et al., 1991).
The first observations of the role of substance ratios for the phytoplankton development have been made as early as in the thirties (Pearsall, 1930). Significant are Smith's works (Smith, 1983; 1986): he analyzed the data from tens of lakes of the world and discovered that the fraction of the blue-greens in the lake algocoenoses falls down abruptly as the atomic N/P ratio exceeds the value of 25. Tilman (1982) called the discovered law “a dramatic influence of the N/P ratio on the taxonomical composition of lakes”. The widely known experiments in the small lakes of Sweden, conducted for many years (Schindler, 1977; Findley and Kasian 1987), have also shown that the N/P variation led to a change in the reservoir blooming type. The dependence of a high abundance of the blue-greens on low values of the N/P ratio (or the dependence of a high abundance of the greens on high N/P values) has been noticed in the lakes of the USA (McQueen and Lean, 1987; Stockner and Shortreed, 1988), South-Eastern Asia (Cho et al., 1990), South Africa (Haarhoff et al., 1992). The inverse proportionality between the abundance of the blue-greens and the N/P value has been established with the aid of statistical correlation analysis for many lake ecosystems (Varis, 1991).
One of the possible mechanisms of such N/P-dependences of the abundances of blue-green and green algae can be represented by the dependence of the optimal N/P ratio on the ratio of the corresponding cellular demands, revealed by the theorem of maximum species abundances (in the cases when this ratio is high for the green algae, dominant in the coenoses, and is low for the blue-greens).
The model and empirical data on the role of the N/P ratio for the species and size structure of phytoplankton communities have made it possible to formulate the conception of directed reservoir blooming control with the aid of biogenic manipulation (Levich, 1995a; 1996). In the de-eutrophication problems, regulation with the aid of the N/P ratio leads to an opportunity of paradoxical control. Namely, the conventional way of de-eutrophication is to lower the phosphoric load (arrow AB in Fig. 1). If, however, it is indeed the low N/P ratio that is essential for the dominance of cyanobacteria, rather than the absolute doses of the nutrients, then one can achieve a transition from reservoir blooming with the blue-greens to blooming with, e.g., Protococcales, by adding nitrogen compounds to the reservoirs (arrow AC in Fig. 1), which is both technically and economically much easier than to extract phosphorus or to restrict its presence in the flows. The additional primary production emerging due to enhanced doses of nutrients (now as the biomass of the Protococcales) may be easily utilized and turned into secondary production by consumers (for example, by fishes eating phytoplankton, specially introduced in the reservoir), since green algae, unlike many taxons of the blue-greens, do not form a trophic dead end and are, as a rule, not toxic. Moreover, a transition from the domain of one-factor limitation (point A in Fig. 1) to that of two-factor limitation (point C in Fig. 1) guarantees the absence of accumulation of the nutrients in the medium due to their full balanced consumption.
The regulation of the phytoplankton community composition may turn out to be useful as well in the case of optimization (by species or biochemical composition, or by size structure) of forage phytoplankton communities for invertebrate breeding, herbivorous fish breeding and other forms of aquaculture (Levich et al., 1996a,b).
An increased proportion of the blue-greens due to a lowered environmental N/P ratio may turn out to be useful for sewage disinfection if sewage waters are to be used for sprinkling or in order to improve the biological properties of sprinkling waters.
4.4. Interpretation and discussion of the extremal principles. Gibbs's theorem
Extremized invariant and the entropy
The functional ![]() , extremized in the above variational problems and called the generalized entropy in Sec. 3, was obtained as a logarithm of the specific invariant which has emerged while ordering the mathematical structures describing the system. The similarity between the quantity H and Boltzmann's entropy is not by accident, since both structure invariants and the statistical entropy are calculated as the numbers of certain transformations (in the case of statistics they are treated as “microstates”). However, our functional, obtained from functor comparison of structures, is in no way connected with a statistical context: its application requires neither large abundances ni, nor a large number of species w.
, extremized in the above variational problems and called the generalized entropy in Sec. 3, was obtained as a logarithm of the specific invariant which has emerged while ordering the mathematical structures describing the system. The similarity between the quantity H and Boltzmann's entropy is not by accident, since both structure invariants and the statistical entropy are calculated as the numbers of certain transformations (in the case of statistics they are treated as “microstates”). However, our functional, obtained from functor comparison of structures, is in no way connected with a statistical context: its application requires neither large abundances ni, nor a large number of species w.
A concrete form of the generalized entropy depends on the type of transformations admitted by the structure of the system under study. Some variants of functor invariants of structures are collected for illustration in Table 4 (Levich, 1982; Levich and Solov’yov, 1999).
A substitution of a solution to the problem (1) — the species structure formula (3) — to the entropy formula leads to a representation of the entropy as a function of the resources limiting the system development:
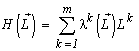 .
.
In the thermodynamical case, when I deal with a maximum entropy of a gas, with the only restriction by the heat flow L1 є DQ, I obtain H = DQ/T, where 1/T є l1 is the corresponding Lagrange multiplier. This establishes a relation between the "generalized entropy" H and the entropy in phenomenological thermodynamics.
Thus the extremal principle that I have applied can be treated as one of the modifications, or, if it turns out to be acceptable, a ground for the maximum entropy principle (Boltzmann, 1964; Gibbs, 1902; Jaynes, 1957; Feynman, 1972; Levine and Tribus, 1978; Haken, 1988; Gzyl, 1995), which is most widely applied in the most different fields, from pure mathematics and theoretical physics to ecology and linguistics.
Other thermodynamical extremal principles are equivalent to the entropy principle:
A maximum of the entropy H with an energy E restriction leads to a minimum of the Lagrange function F = E - TH, which is called in thermodynamics free energy (a relation between the absolute temperature T and a Lagrange multiplier was indicated two paragraphs before).
The quantity e = T(Heq - H), where Heq is the entropy of the system in the thermodynamical equilibrium state, is called in thermodynamics exergy (i.e. the energy that can be converted into useful work with the participation of a given environment). S. JØ rgensen (1986; 1988; JØ rgensen et al., 1995) has put forward and successfully applied the maximum exergy principle in the context of ecological modelling: changes in the influence upon a system will cause the system structure changes accompanied by non-negative exergy changes. The exergy value coincides up to a constant factor with the "generalized entropy", the logarithm of the specific invariant of the system which is extremized in our approach. Thus the extremal principle proposed in the present work is a modification of S. JØ rgensen's maximum exergy principle, supplemented by a non-thermodynamical method of entropy calculation.
Complexity, information, self-organization, expansion, measure of structuredness, “stability”, diversity
The entropy origin of the functional H creates for it some more possible interpretations:
A system complexity measure.
The amount of information contained in the system structure (Levich, 1978; JØ rgensen, 1995; Bastianoni and Marchettini, 1997).
The degree of the system's self-organization (Klimontovich, 1995; Levich, 1995b).
In its original formulation (Section 3), the extremal principle under consideration is postulated as a realization of system states with an extremal structure. The construction of a comparison between structured sets (Bourbaki, 1956; Levich, 1982; Levich and Solov’yov, 1999) is similar to that of cardinality comparison between structureless sets. Therefore the extremal principle proposed here generalizes the maximum expansion principle (within the resources available), which is conventionally applied in biology to separate populations, to communities of many species.
The functional ![]() may be characterized as a measure of the community structuredness, i.e., the degree of remoteness of the set's partition from its structureless analogue. In this way to the formulation of the extremal principle as that of the realization of an extremal structure returns.
may be characterized as a measure of the community structuredness, i.e., the degree of remoteness of the set's partition from its structureless analogue. In this way to the formulation of the extremal principle as that of the realization of an extremal structure returns.
For systems with the same basic set cardinality n, the value of the specific invariant  will be the greatest if the denominator
will be the greatest if the denominator  is the smallest. This quantity is the number of transformations admitted by the system structure (in this case, the structure of a partition into non-intersecting groups of individuals). Thus the extremal principle reduces to the requirement that a state with a minimal number of admissible states be realized, or, in the above sense, a state with the most “stable” structure.
is the smallest. This quantity is the number of transformations admitted by the system structure (in this case, the structure of a partition into non-intersecting groups of individuals). Thus the extremal principle reduces to the requirement that a state with a minimal number of admissible states be realized, or, in the above sense, a state with the most “stable” structure.
The quantity 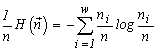 is used by ecologists as the diversity index of the species structure of a community (McArthur, 1955). I would like to note that a consideration of communities with other admissible transformations than those adopted in our model (Section 3) leads to expressions for the structure invariants which coincide with other known diversity indices (see more details in section 5.1). The above identifications make it possible to interpret our extremal principle as the requirement of a maximum species diversity in a community (see e.g. Lurie et al., 1983).
is used by ecologists as the diversity index of the species structure of a community (McArthur, 1955). I would like to note that a consideration of communities with other admissible transformations than those adopted in our model (Section 3) leads to expressions for the structure invariants which coincide with other known diversity indices (see more details in section 5.1). The above identifications make it possible to interpret our extremal principle as the requirement of a maximum species diversity in a community (see e.g. Lurie et al., 1983).
The Gibbs theorem
It can be shown (Levich and Alexeyev, 1997) that the problem (1)
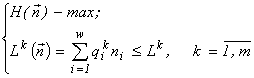
for each ![]() is equivalent to the problems
is equivalent to the problems

It thus turns out that, instead of the formulation of the extremal principle as “the system entropy is maximum under the condition that the resource consumption is lower than a certain deposit”, another formulation is valid: “the resource consumption by a system is minimum under the condition that the system entropy (or its complexity, diversity, etc.) is higher than a certain threshold”, i.e., the maximal entropy principle is equivalent to the principle of minimal consumption of limiting resources. The theorem indicated is a generalization of the Gibbs theorem (Gibbs, 1902) that the requirement of maximum gas entropy (for given energy) is equivalent to the energy minimization procedure (for given entropy).
5. Ecological meaning of the model constructs
5.1. Origin of rank distributions
If one enumerates the groups of organisms by decreasing abundances, then the number i of a group is called its rank, and the rank dependence of the abundance n(i) is called a rank distribution. The rank distributions of abundances (or biomasses) are an effective tool for quantitative studies of the structure of ecological communities and for normalizing the structure-violating influences.
One may consider as groups such sets as biological taxons, size classes, or any sets of individuals united by physiological or other indications. The reviews concerning applications of rank distributions in ecology (Levich, 1980; Frontier, 1985; Puzachenko, 1996) contain a great number of references to studies of communities of plankton, benthos, periphyton, birds, mammals, insects, higher plants and many other organisms.
Various approximations are used in ecology for phenomenological descriptions of rank distributions (Levich, 1980): the exponential model, n(i) ~ ![]() ; the hyperbolic model, n(i)
; the hyperbolic model, n(i) ![]() ; the zeta distribution that unifies them n(i) ~
; the zeta distribution that unifies them n(i) ~![]() ; the “broken rod” model, n(i) ~
; the “broken rod” model, n(i) ~ ![]() (where n(i) denotes the number of individuals of the rank i; z, b and B are model parameters).
(where n(i) denotes the number of individuals of the rank i; z, b and B are model parameters).
The species structure formula (3) (see Section 4.2) explains the origin of rank distributions.
Let m = 1, i.e. only one resource is consumed. Let the species' demands for this resource be distributed linearly: qi º
q1i. Then the species structure formula yields the exponential rank distribution, ni /n = zi, where z =![]() (see also examples in Section 4.2). Then, let the species' demands be distributed by the law qi =q1 ln(B + i), then ni /n ~ 1/(B + i)b, where b =
(see also examples in Section 4.2). Then, let the species' demands be distributed by the law qi =q1 ln(B + i), then ni /n ~ 1/(B + i)b, where b = ![]() q1. For such a slowly varying demands distribution as qi ~ lnlni, I obtain a distribution of abundances close to that specified by the "broken rod" model, ni ~ -lni. In the case of two resources and the demands distributions
q1. For such a slowly varying demands distribution as qi ~ lnlni, I obtain a distribution of abundances close to that specified by the "broken rod" model, ni ~ -lni. In the case of two resources and the demands distributions ![]() and
and ![]() , I obtain a two-parameter zeta distribution of abundances. The abruptly decreasing form of rank distributions becomes understandable: according to the species structure formula, the abundances depend exponentially on monotone demands distributions. Thus the distribution of abundances is entirely created by the distribution of demands. See also other examples in Section 4.2. Fig. 4 illustrates the empirical rank distributions for phytoplankton.
, I obtain a two-parameter zeta distribution of abundances. The abruptly decreasing form of rank distributions becomes understandable: according to the species structure formula, the abundances depend exponentially on monotone demands distributions. Thus the distribution of abundances is entirely created by the distribution of demands. See also other examples in Section 4.2. Fig. 4 illustrates the empirical rank distributions for phytoplankton.
5.2. Biological diversity
The origin of diversity indices
The rank distribution parameters (the Lagrange multiplies of the model) reflect the abundance decrease rate (abruptness, evenness, uniformity, homogeneity, etc) from group to group, or, which is the same, the degree of dominance of highly abundant groups. These parameters are called the indices of species' (as far as a species distribution is concerned) diversity and are usually calculated using approximate formulae: ![]() (Margalef, 1951) for exponential rank distributions,
(Margalef, 1951) for exponential rank distributions, ![]() for b = 2 (Menhinik, 1964) for hyperbolic distributions,
for b = 2 (Menhinik, 1964) for hyperbolic distributions, ![]() for b = 1 (Odum et al., 1960). These indices are incorporated in the class of parametric ones (Levich, 1980).
for b = 1 (Odum et al., 1960). These indices are incorporated in the class of parametric ones (Levich, 1980).
Another class is formed by imperative diversity indices, like the entropy index  (McArthur, 1955), the Simpson index
(McArthur, 1955), the Simpson index  (Simpson, 1949), or the Pielou index
(Simpson, 1949), or the Pielou index 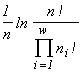 (Pielou, 1975). These indices are unambiguously related to the invariants of mathematical structures which create the functionals of the variational model. The entropy functional has emerged (see Section 3) in modelling of a community by the structure of a partitioned set and mortality and cellular fission as admissible transformations (the correspondences in Table 4 which are injective and surjective, but are not functional and are not everywhere defined). If one admits, in addition to the above ones, such transformations as absorption of some organisms by others and introduction of individuals from outside (arbitrary correspondences in Table 4), then the specific invariant acquires the form
(Pielou, 1975). These indices are unambiguously related to the invariants of mathematical structures which create the functionals of the variational model. The entropy functional has emerged (see Section 3) in modelling of a community by the structure of a partitioned set and mortality and cellular fission as admissible transformations (the correspondences in Table 4 which are injective and surjective, but are not functional and are not everywhere defined). If one admits, in addition to the above ones, such transformations as absorption of some organisms by others and introduction of individuals from outside (arbitrary correspondences in Table 4), then the specific invariant acquires the form 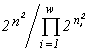 , while the extremized functional — namely, the logarithm of the invariant — is
, while the extremized functional — namely, the logarithm of the invariant — is 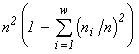 , i.e., turns out to be proportional to Simpson's diversity index. If only invariable existence of individuals is admitted (injective, functional, everywhere defined and surjective correspondences), then the specific invariant of the partitioned sets structure is
, i.e., turns out to be proportional to Simpson's diversity index. If only invariable existence of individuals is admitted (injective, functional, everywhere defined and surjective correspondences), then the specific invariant of the partitioned sets structure is 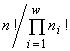 , while the extremized functional turns out to be proportional to Pielou's diversity index.
, while the extremized functional turns out to be proportional to Pielou's diversity index.
Thus the variational model allows one to consciously choose a diversity index that is adequate to the community structure and state. Namely, the imperative diversity indices are determined by the mathematical structure adopted for the description of the community, and by the transformations admitted by its functioning. As for the parametric indices, they are created by extremizing some imperative index and, in addition, depend on the demands (quotas) matrix and on the environmental resource deposits.
The biological diversity theorem
According to the variational model, one can assert that the biological diversity is a consequence of the limited nature of biogenic resources on the Earth. More precisely, the following theorem is valid: under unlimited resources, only one-species communities can exist. Indeed, a solution of the variational problem (1) without resource limitation using Lagrange's method of indefinite multipliers implies the requirement that the partial derivatives of the Lagrange function  with respect to ni and n be zero, which in turn allows one to express ni and n in terms of the multipliers l: ni = n = e l -1 and their substitution to the constraint
with respect to ni and n be zero, which in turn allows one to express ni and n in terms of the multipliers l: ni = n = e l -1 and their substitution to the constraint  gives w = 1.
gives w = 1.
5.3. The ecological meaning of the Lagrange multipliers
The interpretation of the Lagrange multipliers (at least for m = 1) as parametric diversity indices has been demonstrated in Section 5.2.
Another interpretation is connected with the dimensionality of the Lagrange multipliers. Since the exponent of the exponential function in the species structure formula (3) is dimensionless, the dimensionality of the multiplier lk is inverse to that of the demands ![]() . That is, the quantity 1/lk may be proportional to the community-averaged demand for the resource k, having the same dimensionality. (I would note that, in the case of perfect gas thermodynamics, for a given energy one has 1/l = T, where the absolute temperature T is proportional to the mean molecular kinetic energy.)
. That is, the quantity 1/lk may be proportional to the community-averaged demand for the resource k, having the same dimensionality. (I would note that, in the case of perfect gas thermodynamics, for a given energy one has 1/l = T, where the absolute temperature T is proportional to the mean molecular kinetic energy.)
One more interpretation is connected with a theorem of variational modelling claiming that
![]()
(Lancaster, 1968), i.e. the Lagrange multiplier lk is the changing rate of the entropy H due to changes of the resource k, therefore it may be interpreted (Intrilligator, 1971) as the "strength of influence" of the factor k upon the "goal function" H.
6. Conclusion
Works in the field of variational modelling can be continued along several lines.
The category-functor basis of the model requires further development. In particular, a formal rather than heuristic foundation of the formula for a specific invariant is necessary. It is possible to perform calculations of functionals for communities with more complex structure types, e.g., with age or trophic structures.
It is desirable to have a "local" instead of global formulation of the extremal principle, making it possible to describe trajectories of a system rather than only stationary states. A search for dynamical equations may turn out to be promising on the way to choosing dynamical systems whose calculated generalized entropy would be a Lyapunov function.
It is possible to solve variational problems with functionals and limitations other than those used in the present paper; it is possible to formulate and prove the corresponding analogues of the already existing theorems, to formalize the approaches to descriptions of communities consuming mutually interchangeable resources, to obtain models of exploited populations, etc.
It is necessary to continue the experimental verification of the model's consequences; it is necessary, in particular, to perform the above described experiments for testing the Limiting Link Rule. It is of interest to seek physiological mechanisms responsible for the realization of the maximum species abundances theorem in the case of equal ratios of external and internal concentrations of the limiting resources for a given organism.
Another point deserving attention is application of the ideas of ecological variational modelling to the description of technocoenoses or economical system which function under the condition of competition for resources.
Application of the consequences of variational modelling to the ecological normalization problems may be of great importance. The point is that the model constructs (functionals, Lagrange multipliers, solutions of the variational problem) specify certain quantitative laws, and a deflection from these laws may be interpreted as an extent of violation of a system's normal functioning. Many of these constructs, in particular, rank distributions, parametric and imperative diversity indices, are systematically used as integral estimation characteristics in the ecology of communities (Levich, 1980; Levich, 1996a). A variational model allows one to consciously select the characteristics adequate to a situation under study and to obtain a biological-based estimate of the ecological state of natural objects on the norm-pathology scale. On the basis of such an estimate allows onecan, in turn, calculate regional standards of ecologically admissible levels of environmental factors which violate the ecological prosperity (Levich, 1994; Levich and Terekhin, 1997).
References
Ahlgren, G., 1980. Effects on algal growth rates by multiple nutrient limitation. Archiv. f. hydrobiologie, 89: 43-50.
Alexeyev, V.L. and Levich, A.P., 1997. A search for maximum species abundances in ecological communities under conditional diversity optimisation. Bull. of Mathemat. Biology, 59: 649-677.
Bastianoni, S. and Marchettini, N., 1997. Emergy/exergy ratio as a measure of the level of organization of systems. Ecological Modelling, 99: 33-40.
Bendoricchio, G. and JØ rgensen, S.E., 1997. Exergy as goal function of ecosystems dynamic. Ecological Modelling, 102: 5-15.
Boltzmann, L., 1964. Lectures on Gas Theory. California Univ. Press, Berkley.
Bourbaki, N., 1956. Thé orie des ensembles. Paris.
Bulgakov, N.G., 1990. Lightdepending characteristics of microalgae growth. Biologicheskie Nauki (Biology Sciences), 7: 58-64 (in Russian with English abstract).
Bulgakov, N.G. and Levich, A.P., 1999. Environmental biogenic elements and the phytoplankton: the nitrogen-to-phosphorus ratio as an independent regulating factor. Archiv fü r Hydrobiologie, 146: 3-22.
Cho, K-S., Kim, B-Ch. and Heo, W-M., 1990. Recent expansion of bluegreen algal blooms in a nitrogen-rich reservoir, Lake Soyang, Korea. In: Dev. Ecol. Perspect. 21st Cent. 5th Int. Congr. Ecol., 23-30 August, at Yokohama, Yokohama, p.356.
Cohen, D., 1979. Maximizing final yield when growth is limited by time or by limiting resources. J. Theor. Biol., 33: 229-307.
De Groot, W.T., 1983. Modelling the multiple limitation of alagal growth. Ecological Modelling, 18: 99-119.
De Pauw, N. and Naessens-Foucquaert, E., 1991. Nutrient-induced competition between two species of marine diatoms. Hydrobiol. Bull., 25: 23-27.
Droop, M.R., 1973. Some thoughts on nutrient limitation in algae. J. Phycol., 9: 264-272.
Feynman, R.P., 1972. Statistical mechanics. Institute of Technology, Massachusetts.
Findley, D.L. and Kasian, S.E.M., 1987. Phytoplankton community responses to nutrient addition in lake 226, experimental lakes Area, north-western Ontario. Canad. J. Fish. and Aquat. Sci., 44: 35-46.
Frontier, S., 1985. Diversity and structure in aquatic ecosystems. Oceanogr. and Mar. Biol. Annual. Rev., 23: 253-278.
Gibbs, J.W., 1902. Elementary principles in statistical mechanics. Longmans, N.Y.
Grover, J.P., 1989. Effects of Si:P supply ratio, supply variability and selective grazing in the plankton. An experiment with a natural algal and protistan assemblage. Limnol. and Oceanogr., 34: 349-367.
Gzyl, H., 1995. The Method of Maximum Entropy. World Scientific; Singapore, New Jersey, London, Hong Kong.
Haarhoff, J., Langenegger, O. and Van Der Merwe, P.J., 1992. Practical aspects of water treatment plant design for a hypertrophic impoundment. Water S. Afr., 18: 27-36.
Haken, H., 1988. Information and Self-organization: a Macroscopic Approach to Complex Systems. Springer, Berlin.
Holm, N.P. and Armstrong, D., 1981. Role of nutrient limitation and competition in controlling the populations of Asterionella formosa and Microcystis aeruginosa in semicontinuous culture. Limnol. and Oceanogr., 26: 622-635.
Insarov, G.E., 1975. Ladder model of organisms growth and multiplication. In: "Quantitative Aspects of Growth of Organisms", Nauka, Moscow, pp. 114 - 118 (in Russian).
Intrilligator, M., 1971. Mathematical Optimization and Economic Theory. Prentice-Hall, N.Y.
Jaynes, E.T., 1957. Information theory and statistical mechanics. Phys. Rev., 106: 620-630.
JØ rgensen, S.E., 1980. Lake management. Pergamon Press, Oxford.
JØ rgensen, S.E., 1986. Structural dynamic model. Ecological Modelling., 31: 1-9.
JØ rgensen, S.E., 1988. Use of models as experimental tool to show, that structural changes are accopainied by increased exergy. Ecological Modelling, 41: 117-126.
JØ rgensen, S.E., 1995. The growth rate of zooplankton of the edge of chaos: ecological models. J. Theor. Biology, 175: 13-21.
JØ rgensen, S.E., Mejer, H.F. and Nielsen, S.N, 1995. Emergy, environ, exergy and ecological modelling. Ecological Modelling, 77: 99-109.
Kilham, S.S., 1986. Dynamics of lake Michigan natural phytoplankton communities in continuous cultures along a Si:P loading gradient. Can. J. Fish. and Aquat. Sci., 43: 351-360.
Klimontovich, Yu.L., 1995. Statistical Theory of Open Systems. Moscow, Janus (in Russian).
Lancaster, K., 1968. Mathematical Economics. N.Y.
Levich, A.P., 1978. Information as system structure. Semriotica i informatica (Semiotic and Informatic), 10: 116-132 (in Russian).
Levich, A.P., 1980. The Structure of Ecological Communities. Moscow University Press, Moscow (in Russian).
Levich, A.P., 1982. Sets Theory, the Language of Cathegory Theory and Their Application in Theoretical Biology. Moscow University Press, Moscow (in Russian).
Levich, A.P., 1994. A Biological Concept of Environmental Control. Doklady Biological Sciences, 337: 360-362.
Levich, A.P., 1995a. Ecological Approaches to Regulating the Bloom Type in Eutrophic Water Bodies. Doklady Biological Sciences, 341: 170-172.
Levich, A.P., 1995b. Self-organization criteria and control parameters in the ecology of communities. In: Proceedings of the International Conference "Self-Organization Criteria in Physical, Chemical and Biological Systems", Suzdal, pp. 108 - 113 (in Russian).
Levich, A.P., 1995c. Time as variability of natural systems: ways of quantitative description of changes and creation of changes by substantial flows. In: On the Way to Understanding the Time Phenomenon: the Construction of Time in Natural Science. Part 1. Interdisciplinary Time Studies. World Scientific; Singapore, New Jersey, London, Hong Kong, pp.149-192.
Levich, A.P., 1996. The role of nitrogen-phosphorus ratio in selecting for dominance of phytoplankton by cyanobacteria or green algae and its application to reservoir management. J. of Aquatic Ecosystem Health., 5: 1-7.
Levich, A.P. and Alexeyev, V.L., 1997. Extremal principle in the ecology of communities: results and discussing. Biophysics, 42: 525-532.
Levich, A.P. and Artyukhova, V.I., 1991. Measuring requirements of phytoplankton for envinronmental substrate factors. Biology Bulletin of the Academy of Science of the USSR, 18: 86-93.
Levich, A.P. and Bulgakov, N.G., 1992. Regulation of species and size composition in phytoplankton communities in situ by N:P ratio. Russian Journal of Aguatic Ecology, 2: 149-159.
Levich, A.P. and Bulgakov, N.G., 1993. Possibility of controlling the algae community structure in the laboratory. Biology Bulletin of the Russian Academy of Sciences, 20: 457-464.
Levich, A.P. and Lichman, E.G., 1992. Model studies of an opportunity of directed structure change of phytoplankton community. Zhurnal Obshchey Biologii (Journal of General Biology), 53: 689-703 (in Russian with English abstract).
Levich, A.P. and Solov’yov, A.V., 1999. Category-Functor Modelling of Natural Systems. Cybernetics and Systems: an International Journal, 30: 571-585.
Levich, A.P. and Terekhin, A.T., 1997. A method to determining ecosystem normal functioning regions in abiotic factors spaces. Water Resources, 3: 328-335.
Levich, A.P., Alexeyev, V.L. and Niculin, V.A., 1994. Mathematical aspects of variation modelling in ecology of communities. Matematicheskoe modelirovanie (Mathematical modelling), 6: 55-71 (in Russian with English abstract).
Levich, A.P., Alexeyev, V.L. and Rybakova, S.Yu., 1993a. Optimization of the structure of ecological communities: model analysis. Biophysics, 38: 903-911.
Levich, A.P., Bulgakov, N.G. and Nikonova, R.S., 1996a. Rational fertilization of fish ponds populated by different species. Biology Bulletin of the Russian Academy of Sciences, 23: 101-103.
Levich, A.P., Bulgakov, N.G. and Zamolodchikov, D.G., 1996b. Optimization of phytoplankton communities structure. KMK Scientific Press Ltd., Moscow (in Russian).
Levich, A.P., Khudoyan, A.A., Bulgakov, N.G. and Artyukhova, V.I., 1992. On a possibility to control the species and size structure of a community in experiments with natural phytoplankton in vitro. Biologicheskie nauki (Biological sciences), 7: 17-31 (in Russian with English abstract).
Levich, A.P., Lyubimova, E.G. and Martashvili, G.Sh., 1986. Species of substrate-energy factors in laboratory algocoenoses. In: Ecological Forecast, Moscow University Press, Moscow, pp.69-103 (in Russian).
Levich, A.P., Maximov, V.N. and Bulgakov, N.G., 1997. Theoretical and Experimental Ecology of Phytoplankton: community structure and functions management. SAL, Moscow (in Russian).
Levich, A.P., Zamolodchikov, D.G. and Alexeyev, V.L., 1993b. Limiting link rule for multispecies community consuming essential resources. Zhurnal Obshchey Biologii (Journal of General Biology), 54: 271-286 (in Russian with English abstract).
Levine, R.D. and Tribus, M., 1978. The Maximum Entropy Formalism. MTT Press, Cambridge, Mass.
Liebig, J., 1840. Chemistry in its application to agriculture and physiology. Taylor and Walton, London.
Lotka, A., 1922. Contribution to the energetics of evolution. Proc. Nat. Acad. Sci. USA., 8: 147-151.
Lurie, D., Valls, J. and Wagensberg, J., 1983. Thermodynamic approach to biomass distribution in ecological systems. Bull. Math. Biology, 45: 869-872.
Margalef, R., 1951. Diversidad de Especies en las Comunidades Naturales. Publnes. Inst. Bilo. Apl. Barcelona, 9, N5.
Margalef, R., 1958. Temporal succession and spatial heterogeneity in phytoplankton. In: Perspectives in marine biology. Berkley, pp.327-347.
Mauersberger, P. and Straš kraba, M., 1987. Two approaches to ecosystem modelling: thermodynamic and cybernatic. Ecological Modelling, 39: 161-169.
McArthur, R.H., 1955. Fluctuations of animal populations and measure of community stability. Ecology, 36: 533-536.
McArthur, R.H., 1969. Species packing, or what competition minimizes. Proc. Nat. Acad. Sci. USA, 64: 1369-1375.
McArthur, R.H., 1970. Species packing and competitive equilibrium for many species. Theor. Pop. Biol., 1: 1-11.
McQueen, D.J. and Lean, D.R.S., 1987. Influence of water temperature and nitrogen to phosphorus ratios on the dominance of blue-green algae in lake St.George, Ontario. Can. J. Fish and Aquat. Sci., 44: 598-604.
Menhinick, E.F., 1964. A comparison of some species-individuals diversity indices applied to samples of field insects. Ecology, 48: 392-404.
Mitscherlich, E.A., 1909. Das Gesertz des Minimums und das Gesetz des Abnehmenden Bodenertrags. Landw. Jahrb., 38: 595.
Monod, J., 1942. Recherches sur la croissance des cultures bacteriennes. Hermann, Paris.
Nielsen, S.N., 1995. Optimization of exergy in a structural dynamic model. Ecological Modelling, 77: 111-122.
Nielsen, S.N., 1997. Examination and optimization of different exergy forms in macrophyte societies. Ecological Modelling, 102: 115-127.
Odum, E.P., 1983. Basic Ecology. Saunders College Publishing, N.Y.
Odum, H.T., 1971. Environment, Power and Society. Wiley, N.Y.
Odum, H.T., Cantlon, J.E. and Kornicker, L.S., 1960. An organizational hierarchy postulate for the interpretation of species-individuals distrbutions, species entropy and ecosystem evolution and the meaning of a species variety index. Ecology, 41: 395-399.
Patten, B.C., 1995. Network integration of ecological extremal principles: exergy, emergy, power, ascendency, and indirected effects. Ecological Modelling, 79: 75-84.
Pearsall, W.H., 1930. Phytoplankton in the English lakes. I. The proportions in the waters of some dissolved substances of biological importance. J. Ecol., 18: 306-315.
Pielou, E.C., 1975. Ecological diversity. Wiley Interscience Publ., N.Y.-London-Sydney-Toronto.
Puzachenko, Yu.G. and Puzachenko, A.Yu., 1996. Semantic aspects of biological diversity. Zhurnal Obshchey Biologii (Journal of General Biology), 57: 1 - 43 (in Russian with English abstract).
Rhee, G.-Yull., 1978. Effects of N:P atomic ratios and nitrate limitation on algal growth, cell composition and nitrate uptake. Limnol. and Oceanogr, 23: 10-25.
Rhee, G.-Yull and Gotham, J.T., 1980. Optimum N:P ratios and the coexistance of planktonic algae. J. Phycol., 16: 486-489.
Samuelson, P.A., 1974. A biological list-action principle for the ecological model of Volterra-Lotka. Proc. Nat. Acad. Sci. USA, 71: 3041-3044.
Schindler, D.W., 1977. Evolutioh of phosphorus limitation in lakes. Science, 195: 260-262.
Schmelzer, J., Ebeling, W. and Feister, R., 1981. Contributions to the theory of competing predators. II. On the existenve of extremum principles. Stud. Biophys., 82: 157-158.
Semevsky, F.M. and Semenov, S.M., 1982. Mathematical modelling of ecological processes. Gidrometeoizdat, Leningrad (in Russian).
Simpson, E.H., 1949. Measurement of diversity. Nature, 169: 688.
Smith, V.H., 1983. Low nitrogen to phosphorus favor dominance by blue-green algae in lake phytoplankton. Science, 225: 669-671.
Smith, V.H., 1986. Light and nutrient effects on the relative biomass of blue-green algae in lake phytoplankton. Can. J. Fish. and Aquat. Sci., 43: 148-153.
Sommer, U., 1983. Nutrient competition between phytoplankton species in multispecies chemostat experiments. Archiev fü r Hydrobiologie, 96: 399-416.
Stockner, G. and Shortreed, S., 1988. Response of Anabaena and Synechococcus to manipulation of nitrogen:phosphorus ratios in a lake fertilization experiment. Limnol. and Oceanogr., 33: 1348-1361.
Straš kraba, M. and Gnauck, A.H., 1985. Freshwater ecosystems. Modelling and simulation. Elsevier, Amsterdam.
Suttle, C.A. and Harrison, J., 1988. Ammonium and phosphate uptake rates, N:P supply ratios, and evidence for N and P limitation in some oligotrophic lakes. Limnol. and Oceanogr., 33: 186.
Suttle, C.A., Cochlan, W.P. and Stockner, J.G., 1991. Size-dependent ammonium and phosphate uptake, and N:P supply ratios in an oligotrophic lake. Can. J. Fish. and Aquat. Sci., 48: 1226-1234.
Svirezhev, Yu.M., 1991. Phenomenological thermodynamics of interacting populations. Zhurnal Obshchey Biologii (Journal of General Biology), 52: 840 - 853 (in Russian with English abstract).
Tilman, D., 1982. Resource competition and community structure. Princeton, New Jersey.
Varis, O., 1991. Associations between lake phytoplankton community and growth factors — a canonical correlation analysis. Hydrobiologia, 21: 209-216.
Washida, T., 1995. Ecosystem configurations consequent on the maximum respiration hypothesis. Ecological Modelling, 78: 173-193.
Webb, J.N., 1995. Hamilton’s variational principle and ecological models. Ecological Modelling, 80: 35-40.
Zamolodchikov, D.G. and Levich, A.P., 1992. A choice of microalgae species for full utilization of substrate factors in water. Moscow University Biological Science Bulletin, 47: 457-464.
Zamolodchikov, D.G., Levich, A.P. and Rybakova, S.Yu., 1993. A study of the adequacy of category — theoretic model of phytoplankton communities. In: Ecological Monitoring Problems and Ecosystem Modelling. Vol. 15, pp.234-246 (in Russian with English abstract).
Zeide, B., 1991. Quality as a characteristic of ecological models. Ecological Modelling, 55: 161-174.