 ;
;Экологический мониторинг. Часть
5. Учебное пособие под ред. проф. Д.Б.Гелашвили. – Нижний Новгород: Изд-во Нижегородского ун-та, 2003, с. 93-259.Региональный экологический контроль на основе биотических и абиотических данных мониторинга
Н.
Г. Булгаков, А. П. Левич, В. Н. МаксимовМосковский государственный университет им. М.В.Ломоносова, Биологический факультет
В задачи экологического мониторинга входят сбор, хранение, а также анализ данных о природной среде и о влиянии на нее человеческой деятельности.
Сбор данных в России регламентируется методическими руководствами Роскомгидромета, ответственного за экологический мониторинг в стране, и других ведомств (см., например, Руководство по гидробиологическому мониторингу..., 1992; см. также
http://ecograde.bio.msu.ru/opis3.htm; Организация и проведение..., 1992; Экологический мониторинг..., 1998, 2000).Хранение данных происходит как на бумажных (см., например, Ежегодники состояния..., 1981-1991; Ежегодники качества..., 1984-1991; Ежегодные данные..., 1990; Ежеквартальные бюллетени..., 1975-1983), так и на электронных носителях. Из вневедомственных баз
данных мониторинга отметим информационную систему (ИС) "Экология пресноводных вод России" (http://ecograde.bio.msu.ru; см. также Абакумов и др., 2000), основывающуюся на указанных выше "бумажных" публикациях.ИС "Экология пресноводных вод России" включает набор баз данных:
Подробное описание гидробиологических и физико-химических характеристик, представленных в ИС, дано соответственно в табл. 1 и 2. Базы данных охватывают сведения о большинстве крупнейших речных бассейнов России (Северная Двина, Волга, Дон, Кубань, Терек, Обь, Енисей, Ангара, Лена, Амур, Уссури).
ИС реализована в 2-х формах: 1) программа Ecograde для работы в среде Microsoft Access. Эта программа позволяет работать с информационными картографическими материалами, со списками водных объектов, измеряемых переменных; позволяет вводить и редактировать данные, вести их обработку. Для программы созданы разделы "Описание информационной системы" и "Инструкции пользователю". 2) Сайт в сети Internet (http://ecograde.bio.msu.ru), на котором доступны все материалы и функции, содержащиеся в программе Ecograde, кроме ввода и редактирования данных. Встроенный в сетевую версию MySQL-сервер позволяет получать выборки из таблиц баз данных по заданным значениям полей.
Кроме набора баз данных, ИС содержит инструкции пользователю, картографические материалы по гидрографическим районам России с указанием створов отбора проб, информацию о методиках отбора проб и о методах получения оценок качества пресных вод, информацию о программах химического, токсикологического, гидрологического и биологического мониторинга в бассейнах рек России, об индивидуальных сапробностях гидробионтов.
Анализ данных
для целей экологического контроля природной среды решает следующие взаимно дополняющие, но не заменяющие друг друга задачи:индикация экологического состояния природных объектов на шкале "норма-патология";
диагностика, т.е. выявление и ранжирование причин, нарушающих экологическое благополучие;
нормирование воздействий на экосистемы;
прогноз экологического состояния систем на основе предполагаемых значений потенциальных абиотических воздействий;
управление качеством нарушенных экосистем.
Можно привести медицинскую аналогию задачи экологического контроля. Индикация экологического состояния соответствует показателю температуры тела теплокровных организмов, отклонение которой от нормы является неспецифическим симптомом патологического состояния организма. Диагностика соответствует выявлению истинных причин патологического состояния. Нормирование и управление качеством среды соответствуют методам лечения болезни. Отметим, впрочем, что подобная аналогия не подразумевает неправомерного отождествления экосистемного и организменного уровней жизни.
В.Д.Федоров (1970) обратил внимание на важнейшее различие между организмом и надорганизменными системами, которое состоит в том, что организмы — это системы a-типа, в которых "выделяется подсистема, регуляторная связь которой с любым элементом сильнее, чем связь этого элемента с произвольно взятым другим элементом". В r-системах, к которым относятся экосистемы, все связи между элементами равноценны. Вследствие того, что в r-системах нельзя произвести выделение управляющей подсистемы, их относят к классу систем с "пассивным" управлением. Для a-систем функциональные перестройки направлены на поддержание, в конечном счете, постоянства структурных характеристик (например, сохранение специфического внешнего облика системы за счет функционирования механизмов регуляции обмена веществ). Для r-систем структурные перестройки направлены на поддержание постоянства функциональных характеристик. Так, например, изменение соотношения свето- и теплолюбивых видов позволяет поддерживать постоянство продукционных характеристик в течение вегетационного периода при варьировании температурных условий и освещенности.Здесь наиболее существенно то, что указанные различия
a-систем и r-систем имеют следствием соответственно смертность организма и бессмертие экосистемы. Поэтому для организма понятия "нормы" и "патологии" имеют вполне осмысленное содержание, так как действительно есть некоторая объективная шкала, на которой можно провести более или менее четкую границу между нормальным уровнем функционирования организма и его патологическими нарушениями. Эта шкала измеряется близостью к смерти. Поэтому, например, температура тела у взрослого человека выше 400C — несомненный признак патологии и вовсе не потому, что статистическая норма для этого показателя составляет 36.60С, а потому что при 42-430C может наступить смерть (т.е. прекращение функционирования) из-за паралича сердца или кровоизлияния в мозг. В экосистеме же сохранение функции за счет структурных изменений означает, что ее внешний облик (видовой состав сообщества) может кардинально измениться, а продуктивность при этом останется относительно постоянной. Это и есть бессмертие экосистемы, потому что, во-первых, изменение видового состава происходит постепенно и нельзя установить момент, когда, например, мезотрофный водоем превращается в эвтрофный, а озеро — в болото. Во-вторых, в отличие от смерти, процесс экосистемных структурных перестроек обратим. Отсюда следует, что хотя в последнее время все чаще и чаще употребляются термины "здоровье" и "болезнь" экосистемы (о чем более подробно будет сказано в нижеследующем обзоре методов биоиндикации), такие определения по сути бессодержательны, иначе придется признать болото менее "здоровой" экосистемой, чем бывшее когда-то на этом месте озеро. Очевидно, устанавливать параметры нормального состояния экосистемы и некоторого отклонения от этой нормы нужно в применении к определенным практическим нуждам человека (обеспеченности пищей, чистой водой, территориями, предназначенными для рекреационных целей и т.д.).Содержание предлагаемой читателю книги задумано как руководство по количественным технологиям, предназначенным для решения указанных выше задач экологического контроля. Иллюстрирующие примеры в тексте относятся, в первую очередь, к данным по пресноводным экосистемам.
2.1. Трудности современной концепции, основанной на нормативах предельно допустимых концентраций загрязняющих веществ
Действующая в настоящее время система экологического контроля основана на концепции предельно допустимых концентраций загрязняющих веществ (ПДК). Однако известно, что концепция ПДК экологически не обоснована. Перечислим основные недостатки этой концепции (Федоров, 1973; Абакумов, Сущеня, 1991):
— Нормативы ПДК определяются в лабораторных условиях в краткосрочных (дни) и хронических (недели) экспериментах на изолированных популяциях организмов, принадлежащих к небольшому числу тестовых видов, по ограниченному набору физиологических и поведенческих реакций для отдельных факторов без какого-либо учета их возможного взаимодействия, поэтому экстраполяция нормативов ПДК на реальные природные объекты неправомерна.
— ПДК принимаются как единые нормативы для огромных административных территорий (порядка одной шестой части суши), в то время как действие загрязняющих веществ зависит от специфических фоновых, климатических, хозяйственных и многих других характеристик конкретного региона. Вследствие этого использование единых ПДК в районах с различными экологическими условиями в реальной практике невозможно.
Возможна, например, следующая ситуация. В водоеме фоновые концентрации железа на порядок превышают ПДК, однако водные организмы адаптированы к этим концентрациям и требовать у предприятий снижения содержания железа в стоках до ПДК бессмысленно. Содержание же хлоридов в водах значительно ниже ПДК, хотя есть данные о том, что хлориды негативно влияют на некоторые популяции водных организмов. Однако требовать уменьшения концентрации хлоридов в стоках невозможно, поскольку нормативы ПДК не нарушены.— За несколько десятилетий в результате достаточно дорогостоящих исследований для водоемов хозяйственно-бытового назначения
установлено около тысячи ПДК, тогда как число загрязняющих веществ антропогенного происхождения превысило миллионы наименований и ежегодно синтезируется около четверти миллиона новых химических веществ. Кроме того, при попадании в воду или воздух сбросов различных предприятий при их химическом взаимодействии образуются вещества разнообразной химической природы, которые действуют на биоценозы принципиально иначе, чем их составляющие. Более того, в результате происходящих химических реакций и превращений химических элементов в водной среде происходит образование новых соединений, которые могут быть токсичнее исходных ингредиентов. Вредное действие физических, химических и других факторов при их комбинировании может суммироваться (аддитивное или независимое действие), ослабляться (антагонизм) или усиливаться (синергизм). При этом, естественно, синергическое действие факторов представляет наибольшую опасность для организмов. Согласно обобщенной концепции синергизма (Петин и др., 1999), при комбинированных воздействиях факторов происходит образование дополнительных повреждений за счет взаимодействия субповреждений, индуцируемых каждым из агентов и не являющихся значимыми при раздельном воздействии каждого из факторов. Показано, что существует оптимальное соотношение воздействующих агентов, при котором повреждающий эффект максимален. Чем меньше интенсивность одного фактора, тем меньшая интенсивность другого фактора должна использоваться для проявления максимального повреждающего эффекта. Анализ аддитивного взаимодействия факторов актуален при нормировании воздушных загрязнений. Так, выявлена особенно высокая зависимость внутриутробной смертности эмбрионов у матерей в Сан-Паулу (Бразилия) с индексом, отображающим совместное действие концентраций в воздухе NO2, SO2 и CO, по сравнению с концентрациями каждого из веществ в отдельности (Pereira et al., 1998). Подобный эффект был замечен в отношении сочетанного воздействия радионуклидных и химических загрязнений на перестройку генома и изменение свойств внутриклеточной среды у человека, мышевидных грызунов и растений (Бурлакова и др., 1998). Заметим также, что не более 10% от общего числа нормированных по ПДК веществ обеспечено методами обнаружения на уровне ПДК (Абакумов, Сущеня, 1991).— На организмы, помимо химического загрязнения, оказывают негативное влияние многие другие факторы, например, тепловое, радиационное, электромагнитное или биологическое загрязнения. И хотя контроль за подобными "нехимическими" воздействиями в принципе возможен в лабораторных условиях, в реальности никто не занимается определением соответствующих ПДК из-за больших материальных затрат, связанных с такими опытами.
— Необоснованным выглядит также один из основополагающих принципов концепции ПДК, указывающий на абсолютную универсальность полученных нормативов, пригодность их для любой природной зоны, любого времени года, любого местообитания (например, при разработке рыбохозяйственных ПДК не учитывается даже разница между лентическими и лотическими водоемами). В самом деле, каждая экосистема обладает эволюционно обусловленным уникальным комплексом связей между отдельными компонентами, специфическим адаптационным потенциалом к возможным опасным воздействиям, выработанной со временем токсикорезистентностью.
Оценка состояния природных объектов по уровням ПДК фактически является неоправданной экстраполяцией границ толерантности тестовых организмов по отношению к изолированным воздействиям на существенно многовидовые экосистемы, где действуют одновременно сложные комплексы десятков и сотен факторов самой разной природы, и которые находятся (в отличие от стандартных лабораторных популяций) в совершенно различных фоновых условиях функционирования.
Отсутствие соответствия между лабораторными и природными моделями экосистем приводит к тому, что ПДК часто оказываются завышенными (Жигальский, 1997). В качестве примера можно привести ситуацию, когда, несмотря на удовлетворительные результаты гидрохимического анализа (т.е. соблюдение ПДК) в водоемах заповедника “Большая Кокшага” (республика Марий Эл), проведенный гидробиологический мониторинг показал тенденцию к ухудшению экологического состояния пойменных участков реки, что выражалось в изменении структуры зоопланктонных сообществ (Дробот, 1997). Известны и обратные ситуации — например, состояние сообщества зоопланктона (
индексированное по стабильности видового состава) в реке Суре в 1993-1997 оставалось благополучным и при превышении ПДК большинства измеряемых физико-химических показателей (Максимов и др., 2000).Перечисленные недостатки концепции ПДК ставят под сомнение дееспособность всей существующей системы экологического контроля — методов диагностики, нормирования, прогноза, управления, а вместе с ними — экономических, правовых и социальных инструментов природоохранной деятельности. Недостатки концепции ПДК известны давно и конструктивная постановка проблемы состоит не столько в критике устаревшего подхода, сколько в конкретной разработке комплекса методов, способных заменить существующие методы контроля.
2.2. Биотическая концепция контроля природной среды.
Альтернативой методологии ПДК, биологической основой которой является существование пределов толерантности для отдельных организмов, могла бы служить концепция экологической толерантности, устанавливающая допустимые уровни воздействий для биотической части реальных экосистем. Согласно предлагаемой концепции (Максимов, 1991а) для любой экологической системы можно найти такие пределы изменений экологических факторов, при которых сохраняют относительную стабильность признаки, отличающие эту экосистему от других, соседних, экосистем. В указанном смысле можно отождествить пределы экологической толерантности с границами, внутри которых состояние экосистемы можно считать нормальным. Тогда по отношению к загрязняющим веществам-ксенобиотикам нижний предел толерантности устанавливается автоматически: это их полное отсутствие в экосистеме. Верхний предел толерантности можно тогда считать экологически допустимым уровнем загрязнения.
Представление о пределах толерантности широко известно в экологии, но в приложении к индивидуальным организмам и экологическим популяциям. Механическое перенесение этого представления на сообщества и экосистемы неправомерно, так как они отличаются от индивидуальных организмов прежде всего принципами самоорганизации. Вследствие этого при выходе какого-либо фактора за пределы толерантности у организма, как говорилось, наблюдается изменение функциональных показателей его состояния при неизменных показателях его состава и структуры, т.е. морфологических признаков (даже в тех крайних случаях, когда наблюдается гибель организма). В противоположность этому любое изменение внешних условий вызывает в сообществе (а значит и в экосистеме) прежде всего структурные изменения (изменение обилия видов, трофических группировок, размерного и возрастного состава и т.п.) при относительном постоянстве таких функциональных показателей, как продуктивность, скорость деструкции и других процессов экологического метаболизма (Федоров, 1970). В силу этого при чрезмерном отклонении внешних условий от некоторой внешней “нормы” наблюдается достаточно постепенное превращение одной экосистемы в другую, такое, что его нельзя характеризовать, как гибель.
Следует упомянуть и о другом отличии экосистем от организма, которое хотя и не носит столь принципиального характера, как только что рассмотренное, но, тем не менее, должно быть принято во внимание при разработке методологических основ изучения экосистем. Оно заключается в том, что пределы толерантности организма или популяции можно установить непосредственно в эксперименте, в котором любой экологический фактор можно варьировать в достаточно широких пределах, испытывая в частности и такие уровни этого фактора, при которых возможна гибель по крайней мере некоторой части особей изучаемой популяции. Очевидно, что подобный эксперимент немыслимо провести с какой бы то ни было природной экосистемой. Отсюда следует, что по сути дела единственным способом установления пределов толерантности экосистемы по отношению к любым экологическим и ксенобиотическим факторам может быть достаточно широкомасштабное и регулярное наблюдение за этой экосистемой, т.е. экологический мониторинг.
Другими словами, речь идет о пассивном “эксперименте”, который человечество в течение длительного времени проводит в местах своего проживания и хозяйственной деятельности не на отдельных организмах, а на популяциях и сообществах, реально населяющих природные экосистемы; не с изолированным химическим веществом, а с полным комплексом действующих на биоту данной экосистемы факторов (химических, гидрологических, климатических, радиационных, биологических и т.д.); в условиях конкретного региона с учетом его фоновых и других локальных характеристик; не при краткосрочном воздействии, а в реальном масштабе времени с учетом запаздывания реакций и накапливания эффектов.
Появляется возможность сменить “химический” (основанный на методологии ПДК) подход к осуществлению экологического контроля на биотический подход (Левич, 1994), основанный на концепции экологической толерантности (Максимов, 1991а) и на представлениях о приоритете биологического контроля (Абакумов, 1991). Эта концепция предполагает существование причинно-следственной связи между уровнями воздействий на биоту и откликом биоты. Задача биотического подхода — выявить в пространстве абиотических факторов границы между областями нормального и патологического функционирования природных объектов. Такие границы предлагаются взамен нормативов ПДК и называются экологически допустимыми уровнями (ЭДУ) нарушающих воздействий. Согласно биотическому подходу, оценки экологического состояния на шкале “норма-патология” должны проводиться по комплексу биотических показателей, а не по уровням абиотических факторов. Абиотические же факторы (загрязнения, другие химические характеристики, климатические показатели, интенсивности переносов и др.) должны рассматриваться как агенты воздействия на популяции организмов, на экологические связи между ними и как потенциальные причины экологического неблагополучия.
Для реализации биотического подхода необходим набор методов получения оценок состояния сообществ, с помощью которых можно было бы отличить экологически благополучную экосистему от экосистемы, в которой произошли существенные изменения, вызванные внешними (в первую очередь — антропогенными) воздействиями. Тогда на некоторой шкале состояний сообществ можно будет установить границы “нормы” и “патологии”. Впрочем, ввиду упомянутых выше принципиальных различий между экосистемой и организмом, в данном случае лучше говорить об установлении границ стабильного существования экосистемы, т.е. таких пределов изменения биотических параметров, при которых экосистема “сохраняет свое лицо”. Систематический контроль за изменением выбранных оценок состояния и должен составлять основу биологической части экологического мониторинга.
Другая группа методов должна обеспечить выявление тех физико-химических характеристик экосистемы, которые ответственны за изменение состояния сообщества и его выход за установленные границы стабильного существования. Это, очевидно, должны быть математические методы анализа, позволяющие выделить в многомерном пространстве экологических факторов область экологического благополучия. Речь здесь может идти, разумеется, только о тех факторах, которые контролируются в соответствии с химической составляющей программы экологического мониторинга. К этой же группе следует отнести и те математические методы, с помощью которых можно установить ЭДУ для обнаруженных повреждающих воздействий.
Отметим, что речь идет об анализе данных экологического мониторинга реальных природных объектов, т.е. об анализе огромных массивов экологических данных. Такой анализ доступен лишь современным информационным технологиям, включающим компьютерные базы экологических данных.
3. Особенности анализа данных экологического мониторинга
3.1. Трудности приложения математической статистики к анализу данных мониторинга
Фундаментальные знания о закономерностях функционирования естественных надорганизменных систем добывают не только в специально организованных и спланированных экспериментах, но и путем анализа данных экологического мониторинга, полученных с помощью стандартных методик. Однако эти данные не всегда удовлетворяют требованиям метрологии, статистической воспроизводимости и другим условиям, которые позволили бы обоснованно использовать для их анализа традиционные методы математической статистики (Максимов и др., 1999).
Независимо от конечных целей экологического мониторинга и организации соответствующей системы наблюдений результат этих наблюдений всегда представляет собой прямоугольную таблицу. Если значения измеряемых переменных располагать в столбцах, число таких столбцов может достигать нескольких десятков — по числу переменных. Каждая строка в такой матрице будет содержать измеренные значения упомянутых переменных в одной пробе, отобранной в определенный момент времени в определенном месте. Понятно
, что число таких строк может измеряться сотнями. Иначе говоря, исходные данные, полученные по программе мониторинга, представляют собой матрицу размерности m*n, где m — число строк, n — число столбцов, и размерность эта весьма велика.При работе с такими матрицами специалисты по статистическому анализу экспериментальных данных рекомендуют использовать разнообразные методы многомерной статистики. Преимущества этих методов, по-видимому, бесспорны: 1) вместо изучения каждой из переменных в отдельности и ее связей с остальными можно сразу исследовать весь массив данных и получить информацию о влиянии всех переменных и их взаимодействий на изучаемую экосистему; 2) при нынешней всеобщей компьютеризации снимаются все затруднения, связанные с огромным объемом вычислений. Раньше многомерными статистическими методами могли пользоваться лишь сравнительно немногие исследователи, в распоряжении которых были большие вычислительные машины и при них помощники-программисты. Теперь не менее (а то и более) мощный персональный компьютер стоит у каждого экспериментатора на письменном столе, а современные (и весьма популярные!) пакеты прикладных статистических программ, такие как Стадия, Statgraphics, Systat, SPSS,
Statistica и т.п., позволяют осуществлять анализ данных даже в том случае, когда исследователь имеет лишь приблизительное представление об алгоритме соответствующих вычислений и принципах его построения. Достаточно создать файл исходных данных и "загрузить" подходящий программный модуль из пакета, которым данный пользователь располагает, руководствуясь в высшей степени "дружественным интерфейсом", которым снабжен каждый такой пакет.Однако в этой кажущейся простоте заключена и немалая опасность, поскольку далеко не всегда исходные данные удовлетворяют тем, довольно жестким, требованиям, которые предъявляют к ним стандартные статистические методы. В учебниках по статистике эти требования, естественно, всегда оговариваются. Важнейшие из них — нормальность распределений переменных, однородность дисперсий, устойчивость частот. Однако ни в одном из таких учебников мы не видели указаний на то, к чему приводит нарушение этих требований.
В работе В.Н.Максимова с соавторами (1999) проводили исследование эффективности традиционных методов математической статистики при анализе сопряженностей гидрохимических и биотических (численности видов зоопланктона) характеристик на примере экосистемы р. Сура в районе Сурского водохранилища.
Многомерный анализ часто начинают с расчета Пирсоновских коэффициентов парной корреляции, которые отражают сопряженность изменений во времени и пространстве любых двух переменных в исходной матрице данных. Наличие таких сопряженностей между гидрохимическими переменными указывает на некоторые характерные особенности гидрологии в исследуемом водоеме, а наличие статистической связи между отдельными гидрохимическими и биологическими переменными может характеризовать отклик биотической компоненты экосистемы на изменение абиотических условий. Кроме того, в результате расчета коэффициентов корреляции для всех пар переменных мы получаем корреляционную матрицу, которая служит основой для таких популярных методов многомерного анализа, как множественная регрессия, факторный анализ, некоторые модификации кластер-анализа.
Хорошо известно однако, что величина коэффициента корреляции Пирсона, как параметра 2-мерного нормального распределения, отражает тесноту связи между двумя выборками, только если они получены из нормально распределенных совокупностей, а сама связь является линейной. Поэтому прежде чем "запускать" соответствующую вычислительную программу, следовало бы по крайней мере убедиться в нормальности распределения всех переменных в исходной матрице данных. Однако даже в руководствах по многомерной статистике нам не приходилось видеть примеры, где проводилась бы проверка нормальности исходных переменных. Между тем такая проверка не требует особых усилий, поскольку соответствующие вычислительные программы имеются в любом пакете прикладных статистических программ.
Можно, в частности, построить так называемые "ящики-с-усами" (
box-and-whiskers plots) и сразу увидеть такие типичные отклонения от нормальности, как асимметрию распределения и наличие "выскакивающих" или "экстремальных" значений. Хорошим способом проверки является и построение полувероятностных графиков. В качестве наиболее надежного метода проверки нормальности часто рекомендуют расчет асимметрии и эксцесса эмпирических распределений, в особенности, когда объем выборки достаточно велик (что несомненно имеет место в нашем примере). Показатели асимметрии и эксцесса, рассчитанные для всех переменных в исходной матрице данных, приведены также в табл. 3. Наименьшие значения этих показателей обнаруживаются только для кальция, растворенного кислорода и рН. Можно принять, что эти три переменные распределены по закону, близкому к нормальному. Поскольку их показатели асимметрии и эксцесса мало отличаются от нуля, распределения остальных переменных характеризуются отчетливой асимметрией и эксцессом и, следовательно, их никак нельзя рассматривать как нормально распределенные.Чтобы показать, к чему может привести отклонение исследуемых переменных от нормальности, приведем для примера диаграмму рассеяния (рис. 1) для концентраций взвешенных веществ и хрома. Коэффициент корреляции для этой пары переменных равен 0.57 и его статистическая значимость формально очень высока, поскольку он рассчитан по 213 парам значений. Вид диаграммы на рис. 1 заставляет, однако, усомниться в том, что между этими переменными действительно имеется сколько-нибудь существенная связь.
Обратим внимание на “ящики-с-усами” по бокам диаграммы, характеризующие вид распределений переменных. Отклонения от нормальности этих распределений совершенно очевидны. На фоне довольно плотного облака точек в левом нижнем углу диаграммы резко выделяются экстремальные значения,
явно "выскакивающие" и за пределы "усов". Если же исключить эти значения (как иногда рекомендуют в руководствах по статистике), т.е. всего 11 точек из 213, то для оставшихся 202 пар значений переменных “взвешенные вещества” и “хром” коэффициент корреляции будет равен всего 0.22. Формально этот коэффициент отличен от нуля с вероятностью 0.998, что обычно считается очень высоким уровнем значимости, однако следует иметь в виду, что этот уровень определяется для единственной корреляции. Иначе говоря, оценка, которую мы получаем по стандартной программе корреляционного анализа, рассчитывается только для пары “взвешенные вещества — хром” в отсутствие остальных переменных. А в нашей матрице данных, как уже было сказано, 44 переменных, так что корреляционная матрица должна содержать 946 коэффициентов парной корреляции. Поэтому при уровне значимости 1-0.998 = 0.002 можно ожидать, что по крайней мере 1-2 раза величина коэффициента корреляции r = 0.22 может встретиться в такой матрице совершенно случайно. Разумеется, оценки коэффициентов в нашей матрице корреляций нельзя считать полностью независимыми, но тем не менее должно быть понятно, что для каждого из 946 коэффициентов статистическая оценка их значимости должна быть более строгой, чем для единственной пары переменных. По-видимому, для того, чтобы признать отличным от нуля коэффициент корреляции, равный 0.22, нужно принять уровень значимости во всяком случае не более 0.001.Однако даже если признать статистически значимым коэффициент корреляции, равный 0.22, то остается весьма сомнительной его, так сказать, познавательная ценность. Квадрат коэффициента корреляции (коэффициент линейной детерминации) характеризует долю дисперсии переменной
y, объясняемой линейной зависимостью у от х. Несколько огрубляя, это можно интерпретировать, как долю изменений переменной у, связанных именно с изменением х. Поскольку 0.222 = 0.0484, возвращаясь к нашему примеру, можно заключить, что (без учета "диких значений") концентрация хрома в воде примерно на 5% обусловлена содержанием в воде взвешенных веществ или, наоборот, всего 5% изменений концентрации взвешенных веществ в воде непосредственно связано с содержанием в ней хрома.Что же все-таки можно извлечь из рассмотрения диаграммы рассеяния на рис. 1? Прежде всего ясно, что в большинстве случаев концентрации взвешенных веществ в исследованных пробах не выходят за пределы 20-30 мг/л, а концентрации хрома — за пределы 0.010 мг/л. Кроме того, только в 4 случаях из 214 экстремально высокие значения для обеих переменных наблюдались в одной и той же пробе. При этом все эти пробы были отобраны в Сурском водохранилище на станциях
B, D, E, F в мае 1997 г. И еще в 2-х пробах, на станции F в августе 1996 г. и у середины плотины в одной из проб, взятых в апреле 1994 г., экстремальные значения концентрации взвешенных веществ наблюдались одновременно с относительно высокой концентрацией хрома (0.01 мг/л). Вряд ли на этом основании можно заключить, что содержание хрома в воде р. Сура и Сурском водохранилище как-то связано с общим количеством взвеси. Итак, по сути дела все, что мы смогли узнать, сводится к обнаружению "выбросов" взвешенных веществ и хрома. Зато естественным образом возникает вопрос: в какой мере эти самые "выбросы" повлияли на сообщества организмов на упомянутых станциях.При попытке применить анализ корреляций к данным о численности отдельных видов зоопланктона мы сталкиваемся с еще более серьезными затруднениями. Хорошо известно, что показатели обилия видов в пробах чаще всего не подчиняются нормальному закону и их распределение асимметрично. Как видно из табл. 3, и в нашем примере для всех видов, выбранных для анализа, характерна не только сильная асимметрия, но и не менее значительный эксцесс. Поэтому
a priori ясно, что прежде чем рассчитывать коэффициенты корреляции, следует каким-то способом преобразовать исходные данные, чтобы получить их распределение, близкое к нормальному. Однако помимо этого возникает еще проблема т.н. пропущенных значений.Например, в нашей матрице данных
Daphnia cucullata была обнаружена в 67 пробах, а D. longispina — в 83, но только в 37 пробах оба эти вида присутствовали одновременно. Если рассчитать коэффициент корреляции между численностями этих видов, рассматривая отсутствие вида в пробе, как пропущенное значение (т.е. оставив пустыми соответствующие места в таблице исходных данных), то при вычислении все пробы, в которых отсутствовал хотя бы один из двух видов, будут исключены и мы получим коэффициент, характеризующий сопряженность их обилий в 37 пробах, тогда как общее количество проб в нашей матрице — 214. Этот коэффициент практически равен нулю (r = 0.0006). Если заменить пропущенные значения нулями, как это чаще всего делается, то в расчете будут использованы все 214 проб. Коэффициент корреляции при этом оказывается на порядок больше (r = 0.0065), но его отличие от нуля остается статистически незначимым.Однако замена пропущенных значений нулями, когда дело касается численностей видов, представляется разумной только на первый взгляд. Прежде всего, мы при этом лишаемся возможности применить логарифмирование — наиболее популярный метод нормализации асимметричных распределений, поскольку нули не логарифмируются. Но гораздо важнее другое: ведь если ни одна особь данного вида не попала в пробу, это не значит, что его не было в водоеме в момент отбора пробы. В лучшем случае мы можем считать, что его обилие было меньше, чем обилие самого малочисленного вида, обнаруженного в этой пробе. Как правило, этот самый малочисленный вид бывает представлен в пробе единственной особью. Поэтому иногда пропущенные значения вместо нуля заменяют некоторыми условными величинами, скажем 1/5 или 1/6. Правда, при этом такую, пусть малую, численность мы можем приписать и тем видам, которых действительно не было в данный момент в водоеме.
Впрочем, на величине коэффициента корреляции такая замена нуля на любую достаточно малую постоянную величину не сказывается, а отклонение наших данных от нормального закона при этом не уменьшается, так что неплохо было бы убедиться, что найденное выше отсутствие корреляции между численностями
D. cucullata и D. longispina действительно указывает на отсутствие сопряженности в их изменениях.При работе с заведомо "ненормально" распределенными переменными, в частности при описании структуры экологических сообществ, рекомендуется использовать непараметрические методы, среди которых наиболее популярен коэффициент корреляции рангов Спирмена (см. например Михайловский, 1988). Если рассчитать этот коэффициент для той же пары видов, обозначив нулями отсутствие вида в пробе, получим
rS = 0.293, что для 214 сравниваемых рангов отличается от нуля при очень высоком уровне значимости (p<10-4). Если же рассматривать отсутствие вида в пробе, как пропущенное значение, то для 37 проб, в которых встречались оба вида дафний, то корреляция оказывается не только статистически значимой, но и весьма существенной с экологической точки зрения: rS = 0.783 (p<10-6).Итак, в зависимости от того, как мы оцениваем отсутствие вида в пробе и каким методом анализа мы пользуемся при расчете корреляции, мы получаем принципиально различные результаты.
Причина этого становится понятной, если построить диаграмму рассеяния для рангов, рассчитанных по возрастанию численности
D. cucullata и D. longispina так, что отсутствию вида в пробе приписывали средний минимальный ранг. Вид этой диаграммы (рис. 2) показывает, во-первых, что коэффициент линейной корреляции рангов (коэффициент Спирмена) ни в какой мере не характеризует связь между рангами обилия для данной пары видов. Во-вторых, хорошо видна положительная корреляция между рангами в пробах, где оба вида встречались одновременно, что собственно и отражает коэффициент rS = 0.783. Но, кроме того, нельзя не обратить внимание на совокупности точек по краям диаграммы. Они соответствуют пробам, в которых встречался лишь один из двух видов. Расположение этих точек заставляет усомниться в том, что между D. cucullata и D. longispina вообще имеется какая-либо связь, поскольку их число сравнимо с числом проб, содержащих оба вида.Приходится признать, что "классический" метод корреляционного анализа оказывается малоэффективным в применении к данным экологического мониторинга, а поэтому не следует рассчитывать и на то, что с помощью упомянутых выше методов факторного или регрессионного анализа мы получим результаты, имеющие сколько-нибудь внятный экологический смысл.
Вернемся, однако, к диаграмме рассеяния для концентраций взвешенных веществ и хрома (рис. 1). Интересное обстоятельство можно обнаружить при визуальном анализе диаграммы рассеяния, если более внимательно рассмотреть ее левый нижний угол в увеличенном масштабе (рис. 3). Почти все точки на этой диаграмме расположены на горизонталях, соответствующих некоторым округленным значениям концентрации хрома. Из 214 значений величина 0.001 встретилась 14 раз, 0.002 — 37 раз и т.д. Это конечно связано с методическими особенностями способа определения хрома. То же характерно и для ряда других переменных, прежде всего ионов металлов, определявшихся в пробах (
Cu, Zn, Pb, Ni, Mn, Co), а также для нитритов и фенолов. Но это значит, что мы имеем дело не с непрерывными, а с дискретными величинами, и не выполняется еще одно требование большинства традиционных статистических методов и в частности корреляционного и факторного анализа — требование непрерывности измеряемых переменных.3.2. Детерминационный анализ данных.
3.2.1. Процедуры детерминационного анализа.
Перечисленные выше недостатки традиционной статистики не свойственны методу детерминационного анализа (ДА), который позволяет устанавливать связи (сопряженности) между различными переменными — как числовыми, так и нечисловыми (качественными). Технология ДА дает возможность создавать любые новые количественные и качественные переменные. При этом исследователь контролирует признаки вновь создаваемых качественных переменных и, соответственно, в любой момент может откорректировать их. Таким образом, ДА становится незаменим в ситуациях, когда необходимо найти связь изменений одной переменной с изменениями другой, если одна из них или обе носят качественный характер.
ДА, созданный первоначально для проведения социологических исследований (Чесноков, 1982), в применении к экологическим данным позволяет (Замолодчиков и др., 1992; Булгаков и др., 1992; Максимов и др., 2000; Левич и др., 2001) устанавливать наличие зависимостей между различными компонентами экосистем, включать в анализ как количественные, так и качественные переменные, учитывать совокупное действие многих факторов, ранжировать установленные зависимости по величине собственных критериев значимости, проводить контекстный анализ, т.е. разбивать исследуемый массив данных на части (по территориальному, временному или любому иному признаку) и работать с каждой из частей в отдельности. Перечисленные достоинства метода ДА позволяют относиться к нему как к весьма привлекательному инструменту для решения задач экологического контроля.
При детерминационном анализе данных используется программное обеспечение “ДА-система” (фирма “Контекст”,
http://www.context.ru), обладающеее всеми необходимыми функциями для осуществления экологического контроля.Известно, что для исследования сопряженностей между дискретными величинами (каковыми являются значения биотических и абиотических характеристик, используемых при экологическом контроле) существует специально разработанный метод обнаружения связи между переменными — метод таблиц сопряженности или перекрестных таблиц (
contingency tables, crosstabulation), подразумевающий, как и ДА, введение качественных признаков для количественных переменных. Согласно этому методу, предлагается более или менее произвольно разбивать шкалу измеряемых переменных на классы и подсчитывать частоты попадания результатов измерений в каждый из классов. Те же процедуры реализованы и в ДА. Однако основное преимущество ДА заключается в том, что, в отличие от метода таблиц сопряженности, с его помощью возможно вычисление значений химических или физических параметров окружающей среды, сопряженных с установленными ранее признаками благополучия или неблагополучия биотического компонента экосистемы. В этом и состоит суть решения задачи экологического нормирования нарушающих экологическое благополучие воздействий.Рассмотрим подробнее ДА-технологию, остановившись отдельно на процедурах, используемых при анализе экологических данных. Все эти процедуры реализованы в прикладном пакете программ “ДА-система” (версия 4.0), предназначенном для работы в операционной среде Windows 95 и старше, а также Windows NT.
Типы переменных
. Как уже было сказано выше, характерная особенность данных, к которым применим ДА, в том, что наряду с количественными, числовыми, переменными можно ввести их качественные, нечисловые, признаки. При этом анализ качественных и количественных данных ведется с учетом их специфики, но с помощью единых процедур. Количество и наполненность маркированных определенными качественными признаками интервалов на шкале дискретных значений числовой переменной задается исследователем в зависимости от стоящей перед ним конкретной задачи и исходя из неких априорных представлений о том, какие значения изучаемой характеристики организма, например, считать низкими, а какие — высокими.Анализ правил.
Для установления связи между различными экологическими переменными с помощью процедуры ДА проверяется заданная критериями точности и полноты истинность этой связи (правила). При этом правилом называется условное суждение вида “если x, то y”, где переменная x называется объясняющей переменной, а переменная y — объясняемой переменной. Точность и полнота — это условные частоты данного правила: точность (Т) — доля случаев, когда правило подтверждается, среди всех случаев, когда имеет место объясняющий признак; полнота (П) — доля случаев, когда правило подтверждается, среди всех случаев, когда имеет место объясняемый признак. Другими словами, точность — это частотная оценка достаточности правила, а полнота — частотная оценка необходимости правила. Вычислим, например, точность и полноту для конкретного правила “если значение концентрации фенолов (объясняющая переменная) было высоким, то наблюдалась низкая общая численность зоопланктона (объясняемая переменная)”. Обе переменные в данном случае являются качественными, т.е. заданные диапазоны их значений маркированы некоторыми признаками (“мало” и “много”). Допустим, что для концентрации фенолов количество наблюдений в классе “много” равно 100, а для численности зоопланктона число наблюдений в классе “мало” — 50. Количество совпавших наблюдений составило 40. Следовательно, Т = 40/100 (40%), а П = 40/50 (80%) (рис. 4а). Соответственно, 100%-я точность означает, что все заданные значения объясняющей переменной сопряжены только с заданным значением объясняемой переменной и ни с каким другим (рис. 4б), а 100%-я полнота — что все заданные значения объясняемой переменной встречаются только вместе с заданным значением объясняющей переменной и ни с каким другим (рис. 4в). В качестве объясняющей может выступать и числовая переменная. Тогда с помощью ДА легко получить интервал ее значений, наиболее надежно объясняющий определенный класс качества объясняемой переменной.Анализ данных с заданием контекста.
Контекст в ДА — это набор признаков, выполняющих особую роль. Он ограничивает анализируемые данные подвыборкой только тех наблюдений, которые обладают указанными признаками. Задать контекст — это значит предложить ДА-системе работать так, словно в анализируемом массиве данных не существует никаких других наблюдений, кроме тех, которые обладают выделенными признаками. При анализе экологических данных это бывает полезным, когда необходимо ограничить выборку либо определенным периодом времени, либо определенным географическим местоположением, либо однородными климатическими, хозяйственными, территориальными или иными условиями.Учет совокупного действия факторов.
ДА позволяет проводить анализ данных, когда в качестве объясняющих выступают несколько переменных. Тогда появляется возможность выявить, например, при каком количественном сочетании различных физико-химических факторов достигаются те или иные значения индикаторных биотических показателей. При этом в ДА существует процедура, позволяющая вычислить вклад каждого фактора в суммарную точность и полноту, реализующиеся в случае одновременного учета всех факторов. Если значение вклада данного фактора, например в точность, больше нуля, то изъятие этого фактора из анализа снизит суммарную точность на соответствующую величину; если вклад меньше нуля, то суммарная точность после исключения фактора, наоборот, повысится. Значение вклада в полноту называется существенностью факторов при их совокупном действии. Совместное действие нескольких факторов на биоту может быть проанализировано также с помощью задания контекста, где контекстом будут служить определенные диапазоны значений каких-либо абиотических факторов, или путем объединения нескольких переменных в одну вторичную.Оптимизация количественных переменных.
С помощью ДА решается следующая задача — нахождение на множестве значений числовой переменной интервала, в котором совокупность значений переменной наилучшим образом объясняет некоторое правило. Наилучшим – в том смысле, что точность правила с искомым объясняющим признаком не ниже заданной, а полнота правила максимальна. Соответствующая процедура в ДА называется оптимизацией числовой переменной. Оптимизационные расчеты решают задачу нормирования абиотических переменных, поскольку выбрав в качестве объясняемой переменной какой-либо биотический параметр, свидетельствующий о неудовлетворительном состоянии сообщества организмов, можно для любого фактора окружающей среды определить значения, которые отвечают за возникновение экологического неблагополучия. Если ищется только верхняя допустимая граница оптимизируемой переменной (для водных экосистем — концентрации веществ-загрязнителей, БПК5, ХПК) или нижняя граница (концентрация растворенного кислорода), то график зависимости биотической характеристики от абиотической переменной носит вид, как на рис. 4. В том случае, если неблагополучие биоты связано как со слишком высокими, так и со слишком низкими значениями переменной (концентрации солей азота, фосфора, кальция, магния, калия, марганца, хлоридов, сульфатов и др.), оптимальным должен быть интервал ее значений посередине шкалы (рис. 5).3.2.2 Примеры детерминационного анализа экологических данных
При анализе сопряженностей между видами зоопланктона
D. cucullata и D. longispina весь ряд значений численности каждого из них разбивали на классы “мало” и “много” (Максимов и др., 1999). При этом отсутствие вида в пробе было отнесено к классу “мало”. Таким образом, введение качественной переменной в ДА позволяет не задумываться над тем, как относиться к нулевым значениям — действительно ли их приравнивать к нулю или считать пропущенными. В нашем случае классы для обоих видов не были равнонаполненными, поскольку количество только нулевых проб превышало 50%. Кроме того, к классу “мало” были отнесены значения численности меньше или равные 0.1*103 кл/м3. Высокая численность D. cucullata наиболее достоверно сопряжена с высокой численностью D. longispina. Т. е. из 57 случаев наблюдения высокой численности D. longispina 51% совпал со случаями высокой численности D. cucullata, в то время как из 144 случаев низкой численности D. longispina со случаями высокой численности D. cucullata совпало только 17%. Такое резкое отличие в значениях точности указанных правил свидетельствует о несомненной положительной сопряженности между численностями исследованных видов. Напомним, что традиционный корреляционный анализ не дал определенного ответа на вопрос о связи между D. cucullata и D. longispina (см. раздел 3.1).В работах Д.Г.Замолодчикова с соавторами (1992) и Н.Г.Булгакова с соавторами (1992) детерминационный анализ использовали для выявления зависимости биотических показателей нагульных и выростных прудов с поликультурой карпа и растительноядных рыб (рыбопродуктивности, конечной навески и выживаемости рыбы) от тех или иных переменных гидрохимического и гидробиологического характера.
Исходные данные для статистической обработки по выростным прудам, функционировавшим в режиме поликультуры, были взяты из соответствующих материалов Волжского экспериментального рыбного завода Астраханской области. За период с 1987 по 1990 гг. для двенадцати выростных годопрудов был составлен массив переменных (Булгаков и др., 1992). Термин "годопруд" означает наблюдение в данном конкретном пруду в определенный год, поскольку один и тот же водоем мог быть задействован в разные сезоны. Набор переменных, для которых имелись данные по всем годопрудам, включал следующие блоки:
1) Рыбоводные характеристики
— начальные и конечные навески, плотность посадки, выживаемость, продуктивность отдельно по видам рыб и общая рыбопродуктивность;2) количество внесенных азотных и фосфорных удобрений (сумма за сезон и отдельно за апрель-май, июнь-июль и август-сентябрь);
3) гидрология пруда
— глубина и площадь;4) гидрохимические параметры прудов — содержание кислорода,
pH, перманганатная окисляемость, концентрация азота и фосфора, отношение азота к фосфору в воде;5) абсолютные и относительные биомассы таксонов фитопланктона (хлорококковые, вольвоксовые, зеленые, диатомовые, эвгленовые, цианобактерии) и общая его биомасса;
6) абсолютные биомассы таксонов зоопланктона (веслоногие, ветвистоусые, коловратки) и общая его биомасса;
7) максимальные сезонные биомассы, а также время в сутках от заливки пруда до достижения этого максимума для отдельных таксонов и суммарного фитопланктона.
Для переменных из п.п. 4-6 в виде самостоятельных переменных фигурировали среднесезонные значения соответствующего параметра, а также усреднения за апрель-май, июнь-июль, август-сентябрь.
Всего, таким образом, было проанализировано 138 переменных. Посредством ДА весь ряд из 12 значений для каждой переменной был разделен на два условных класса — "мало" и "много". Разбиение в каждом случае происходило нелинейным образом так, чтобы в каждом классе оказалось не менее четырех и не более восьми значений. При этом граница между классами "мало" и "много" для каждой конкретной переменной принималась исходя из гидрохимических нормативов для рыбоводных прудов, а также из общих представлений о том, какая биомасса фито- и зоопланктона считается высокой, а какая — низкой.
Если высокому значению объясняемой переменной соответствовало высокое значение объясняющей переменной, то такую детерминацию (сопряженность) именовали положительной, если наоборот — отрицательной. Для анализа были отобраны только значимые детерминации, т.е. те, которые соответствуют определенным порогам точности и полноты (соответственно не менее 50 и 60 %).Объясняемой переменной "высокая общая рыбопродуктивность" сопутствовало повышенное содержание азота в удобрениях, но не в воде прудов. Вероятно, активное вовлечение минерального азота в процессы ассимиляции ведет к наблюдаемому снижению его концентрации. Фосфор, как и предполагалось, не требуется в большом количестве для роста ихтиомассы. На рост рыбопродуктивности положительно влияет повышенное содержание кислорода, особенно в конце сезона, а отрицательно — высокая окисляемость. Оказалось также, что наиболее благоприятны весной низкие значения водородного показателя, а осенью — высокие. Последний факт, впрочем, может быть связан с метаболической деятельностью рыб и других гидробионтов.
Так что в данном случае нельзя однозначно ответить на вопрос, что было причиной, а что — следствием. И тогда весьма вероятно, что рыбопродуктивность следует переквалифицировать в объясняющую переменную. В отношении фитопланктона была отмечена положительная сопряженность рыбопродуктивности со среднесезонной биомассой зеленых и с осенней биомассой эвгленовых водорослей. Хлорококковые и диатомовые водоросли сопряжены с высокой рыбопродуктивностью, имея низкую биомассу. Правда, для относительной биомассы хлорококковых картина обратная. Высокая продуктивность сопряжена с малым обилием цианобактерий как по абсолютной, так и по относительной биомассе. Отрицательная детерминация была найдена и для общей массы водорослей. Заметим также, что на повышение рыбопродуктивности влияют также ранние пики цветения вольвоксовых и зеленых водорослей. Среди таксонов зоопланктона положительную сопряженность обнаруживала только биомасса веслоногих раков. У остальных групп и зоопланктона в целом знак сопряженности менялся на протяжении сезона.Большой продуктивности по белому толстолобику соответствовало повышенное количество азотных и пониженное — фосфорных удобрений; высокая концентрация всех минеральных форм азота и низкая — фосфора, и, соответственно, повышенные соотношения этих элементов в воде; увеличенное содержание растворенного кислорода и уменьшенная окисляемость (за исключением конца сезона); большая годовая сумма тепла; повышенная биомасса (абсолютная и относительная) представителей отдела зеленых водорослей и пониженная — цианобактерий. Для диатомовых водорослей существенных детерминаций не найдено, а в отношении эвгленовых положительная детерминация выявлена с низкой относительной биомассой (в среднем за сезон). Примечательно, что в тех случаях, когда пруды обладали высокой продуктивностью по белому толстолобику, чаще всего в них было мало зоопланктона, что согласуется еще и с отрицательной сопряженностью с продуктивностью по пестрому толстолобику. Известно, что последний является основным потребителем зоопланктонной продукции в пруду. Продукция белого толстолобика прямо зависела от его конечной навески и выживаемости, а также от выживаемости пестрого толстолобика, но была отрицательно сопряжена с конечной навеской последнего. Поэтому можно говорить, что весь комплекс указанных факторов влиял прежде всего на конечную навеску, а не на выживаемость: бедность прудов зоопланктоном не стала причиной массового отхода пестрых толстолобиков, но и не позволила существенно прибавить в весе, что и предопределило в конечном счете рыбоводные итоги.
Для высокой продуктивности по пестрому толстолобику практически не существовало положительных сопряженностей ни с количеством удобрений, ни с концентрацией биогенных элементов, ни с кислородным режимом, ни с биомассой фитопланктона и отдельных его частей. Высокому съему продукции этого вида рыб сопутствовала лишь постоянно высокая вторичная продукция копепод, а также коловраток и всего зоопланктона в отдельные моменты сезона.
Единственным таксоном фитопланктона, чья абсолютная биомасса положительно сопряжена с высокой продукцией карпа, стали цианобактерии. Высокая биомасса зоопланктона, главным образом, веслоногих, совпадала с высокой продуктивностью карпа в августе-сентябре. В остальное время никаких положительных сопряженностей не было обнаружено.
При исследований факторов, влияющих на рыбопродуктивность и относительную биомассу зеленых водорослей в 20 нагульных прудах (Замолодчиков и др., 1992), выяснилось, что большая общая рыбопродуктивность наблюдалась при низком и среднем содержании кислорода в воде (все переменные были разделены на три класса "мало", "средне" и "много"). В целом для данной объясняемой переменной было выявлено небольшое количество значимых сопряженностей.
В конце сезона (август-сентябрь), т.е. тогда, когда биомасса рыб доходит до максимума, высокой продуктивности по белому толстолобику сопутствовали низкие концентрации кислорода. Велики также сопряженности с низкими значениями биомассы зоопланктона, который, во-первых, не представляет никакой пищевой ценности для белого толстолобика, во-вторых, может действовать как конкурент за пищевой ресурс.
Следствием высокой продукции пестрых толстолобиков также было пониженное содержание кислорода. Характерно, что для данной объясняемой переменной было выявлено мало сопряженностей с фитопланктонными показателями — микроводоросли, как известно, не являются основной пищей этого вида рыб.
Рыбопродуктивность по карпу была сопряжена с низкой биомассой большинства таксонов фитопланктона. Это доказывает, что в системе трофических связей пруда не наблюдается никакого взаимодействия между микроводорослями и карпом, который питается бентосом и зоопланктоном.
Наиболее важными из переменных, объясняющих высокую относительную среднесезонную биомассу зеленых водорослей, оказались низкие относительные биомассы цианобактерий и пирофитовых водорослей, что свидетельствует о конкуренции за ресурс между двумя последними отделами водорослей и зелеными. Также была отмечена сопряженность с низкой среднесезонной биомассой зоопланктона. В данном случае зеленые водоросли в результате ослабления пресса выедания получают условия для массового развития.
Примеры применения ДА к задачам индикации, диагностики и экологического нормирования приведены в главах 4 и 6.
3.3. Метод функции желательности.
Биотическая концепция экологического контроля подразумевает применение биологических показателей для оценки экологического состояния природных объектов. Такими показателями могут быть численности или биомассы выделенных групп организмов в изучаемом местообитании; характеристики продуктивности; параметры распределения организмов по размерам, биомассе, группам численности; индексы разнообразия; показатели встречаемости организмов в местообитаниях с различной обеспеченностью питательными веществами или с различной степенью загрязненности (индексы сапробности) и многие другие.
Индикация экологического состояния, как правило, требует перевода значений измеренной числами индикаторной характеристики в качественные градации шкалы "норма-патология". Необходимость разбиения количественной шкалы измерения экологической переменной на классы, обладающие лишь качественными признаками, как указывалось выше, существует также при использовании детерминационного анализа данных. Способы разбиения количественных шкал на классы имеют, как правило, экспертный, т.е. не формализованный характер. Существует прием преобразования данных, позволяющий сделать экспертную процедуру более прозрачной. Этот прием состоит в построении "функции желательности", предоставляющий математический инструментарий для отображения количественных шкал в обобщенные шкалы критериев качества.
Присущее функции желательности соотнесение текущего значения той или иной индикаторной характеристики с максимумом (или эталоном) входит в метод Бателя — одну из процедур оценки воздействия на окружающую среду (Вторжение..., 1983). Для целей экологического контроля этот метод осуществляется А.М.Степановым (1986, 1988, 1990, 1991). В другой функции желательности учтено, что наиболее желательна неотличимость текущего состояния от контроля, а повышение обилия индикаторного организма так же нежелательно, как и его снижение (Сахаров, Ильяш, 1982б). В других простых функциях желательности наиболее желательным признается наиболее вероятное (чаще всего встречающееся) состояние (Сахаров, Ильяш, 1982а) или многолетнее среднее (Сахаров, 1982). Удобной и часто используемой в экологии является функция желательности Харрингтона
d = exp(-exp{-y'}) (Калинин и др., 1991; Сахаров, Ильяш, 1982а; Федоров и др., 1982), где y'— кодированное значение признака.Показано, что функция желательности может быть с успехом использована при оценке качества природных вод (Максимов, 1980; Максимов и др., 1983), при оценке состояния лабораторных популяций по комплексу эколого-физиологических показателей (Тамарина и др., 1981), а также как обобщенный показатель состояния сообщества при изучении действия загрязнителей на экосистемы (Симонов и др., 1987, Kaitala, Maximov, 1986). На основе накопленного опыта применения указанного подхода к различным экологическим задачам разработан ряд описанных ниже практических приемов, облегчающих построение шкал частных желательностей с учетом специфики объекта исследования (Носов и др., 1997).
Расчет функции желательности начинают с выбора для каждого экологического фактора шкалы на отрезке от 0 до 1, такой, что значениям этого фактора, наиболее благоприятным для нормального функционирования экосистемы, сопоставляются значения, близкие к 1 (обычно от 0.6 до 1). Тем же уровням фактора, которые по каким-либо соображениям считаются "плохими", даются на шкале желательности значения, близкие к 0 (обычно от 0 до 0.4).
Различают два основных варианта построения шкал желательности: с односторонним и с двухсторонним ограничением. В первом из них задается лишь одно "критическое" значение фактора, например, максимально допустимый уровень какого-нибудь загрязнителя. Тогда результат анализа любой пробы, в которой количество этого загрязнителя превысит установленное ограничение, будет оцениваться величиной желательности, не превышающей 0.4, и чем выше окажется содержание загрязнителя, тем ближе к 0 будет желательность этого показателя. Очевидно, что без особых колебаний мы примем желательность равной 1 в том случае, если загрязнение будет полностью отсутствовать в пробе.
Естественно, что для некоторых факторов единственное ограничение может быть установлено снизу. Например, в водоемах чаще всего обращают внимание на нежелательность снижения концентрации растворенного кислорода. В этом случае минимальным значениям содержания кислорода будут соответствовать и минимальные значения желательности.
Для большинства же биотических и абиотических факторов в принципе должны быть установлены как минимальные, так и максимальные допустимые уровни. Способ их установления зависит от степени изученности той конкретной экосистемы, для которой они определяются. В качестве первого приближения мы считаем, что проще всего строить шкалу желательности на основе эмпирической функции распределения соответствующего экологического параметра.
Оценки желательности каждого из показателей, полученные по предлагаемому методу, образуют матрицу той же размерности, что и матрица исходных данных. Эта новая матрица может быть проанализирована любым из стандартных методов многомерного анализа. При этом, между прочим, преодолеваются трудности, связанные с различиями в размерности физически разнородных факторов. Если, к примеру, достаточно нелепо выглядит вопрос: "Что больше — температура 15
0С или соленость 250/00?", то абсолютно осмысленным будет сравнение желательности для температуры dt = 0.7 и желательности для солености ds = 0.2, если для какого-либо конкретного региона Мирового океана температура 150C близка к обычной в данный момент времени, а соленость — значительно ниже, чем нормальная (350/00).Для предварительной, своего рода рекогносцировочной, оценки экологической ситуации достаточно рассчитать обобщенную желательность:
D =Величина этой обобщенной желательности может служить некоторой интегральной мерой отклонения состояния экосистемы от нормы. В идеальном случае для абсолютно ненарушенной экосистемы величина
D должна быть равна 1, а если хотя бы одна из величин di окажется равной 0, очевидно, что и D = 0 (подробнее об этом см. Максимов, 1980).Возможны следующие способы построения функций желательности:
— через указание наиболее желательного значения на основе вида эмпирической функции распределения измеряемой величины;
— по левой и правой границам диапазона желательных значений;
— по левой границе и месту расположения оптимальной желательности;
— по правой границе и месту расположения оптимальной желательности.
После выбора способа построения функции желательности строится эмпирическая функция распределения рассматриваемой величины и соответствующая ей вероятностная функция. На графике функции распределения (рис. 6) можно установить требуемое значение переменной. После ввода всех параметров функции желательности строится ее график. По горизонтальной оси откладываются измеренные значения, по вертикальной — соответствующие им желательности.
Используемые для расчетов формулы являются частными случаями общей формулы для функции желательности, многократно описанной в литературе (см. например: Адлер и др., 1976). Перечислим эти формулы для каждого из вышеприведенных способов построения желательностей.
Построение функции желательности по эмпирической функции распределения на основе задания наиболее желательного значения. Пусть
x ® Fэксп(x) экспериментальная функция распределения случайной величины x. Обозначим через y(z) функцию для z Î [0,1].y(z) = 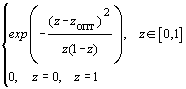 ;
;
Тогда искомая функция желательности есть суперпозиция функций
G(x) = y(Fэксп(x)). Единственным параметром, задаваемым при указанном способе построения желательности, является выбор числа zопт из диапазона [0,1].Смысл такого преобразования сводится к стандартизации исходной переменной и при этом величина желательности получается тем ближе к 1, чем меньше отклонение
x от некоторого значения, принятого нами за оптимальное. Выбор соответствующего числа zопт делается на основе эмпирической функции распределения величины x, что в известной мере отражает представление о статистической норме, как о таком интервале значений экологического показателя, в котором они чаще всего наблюдаются в длительно существующей ненарушенной экосистеме.Построение функции желательности по месту расположения левой и правой границ диапазона желательных измерений. Пусть значения
xлев и xправ определяют диапазон желательных измерений рассматриваемой величины. Обозначим через z(x) вспомогательную функцию от x ® z(x) = . Тогда желательность в точке x будет вычисляться по формуле G(x) = exp (- z2(x)).
. Тогда желательность в точке x будет вычисляться по формуле G(x) = exp (- z2(x)).
Построение функции желательности по левой границе и месту расположения оптимальной желательности.
Учитывая сделанные ранее обозначения, введем вспомогательную функцию x ® z(x) =Построение функции желательности по правой границе и месту расположения оптимальной желательности.
Желательность вычисляется по той же формуле, что в пункте 3, только во вспомогательной функции xлев заменяется на xправ.В приведенных ниже примерах использованы данные гидрохимических анализов 94 проб, собранных при оценке качества вод в ряде малых рек Московской области. Среди множества измеренных показателей были выбраны такие общепринятые параметры качества пресных вод, как БПК
5 (биохимическое потребление кислорода за 5 суток) и концентрация растворенного кислорода.На рис. 6 показана функция распределения переменной БПК
5, использованная при выборе параметров для двухстороннего ограничения. Вид графика соответствует тому моменту, когда уже задана левая граница допустимых значений (в этом примере произвольно взято значение хлев = 1.953) и происходит установка верхней границы xправ = 5.122. Данные границы соответствуют благополучному классу качества вод по БПК5 в соответствии с 6-балльным классификатором качества по гидрохимическим показателям (Оксиюк и др., 1993). На графике при этом проведена вертикальная линия, указывающая положение верхней границы на оси абсцисс.На рис. 7 показан график функции желательности, рассчитанной для переменной БПК
5 при выбранных таким образом двухсторонних границах. По этому графику легко видеть, что наивысшая желательность, т.е. "благополучные" значения БПК5, относятся к интервалу вблизи средних и медианных величин (т.е. значений в диапазоне 2.9-4 мг О2/л). Самые же большие и самые малые значения (выше 5.5 мг О2/л или ниже 1.8 мг О2/л) принимаются в данном случае за совершенно нежелательные и им приписываются значения желательности, близкие или практически равные 0.Вариант с ограничением слева для переменной "Концентрация кислорода" показан на рис. 8. Вполне естественно, что для содержания в воде кислорода его максимальная концентрация (в данном примере 14.83 мг/л) принята за оптимальное значение. В качестве минимально допустимой в данном примере принята концентрация 7 мг/л.
На рис. 9 для той же переменной построена функция желательности, основанная лишь на эмпирической функции распределения переменной "Концентрация кислорода" в исследованных пробах и при условии, что за оптимум принято значение концентрации 8.366 мг/л, близкое к медиане и среднему арифметическому. Этот пример моделирует ситуацию, когда
a priori ничего не известно о значении некоего показателя для обследованной экосистемы, а в расчет принимается лишь приведенное выше соображение, что в благополучной экосистеме любой показатель ее состояния чаще принимает значения внутри интервала его возможных изменений и реже — на концах этого интервала.4. Индикация состояния экосистем по биотическим показателям
4.1. Экспертные оценки
Общепринятый подход к оценке экологического состояния природных объектов в мировой практике экологического контроля отсутствует. Существующие методы различны для различающихся биотопов и программ мониторинга (Воробейчик и др., 1994; Булгаков, 2002). Наиболее употребительны способы индикации, основанные на экспертных оценках.
В качестве одного из примеров приведем классификатор качества пресных вод, используемый в системе экологического контроля Роскомгидромета (Организация и проведение..., 1992). Классификатор (табл. 4) оперирует, в частности, балльными индексами (индекс сапробности, биотический и олигохетный индексы), которые в свою очередь являются экспертными оценками экологического качества вод для отдельных групп организмов. Индекс сапробности для фито-, зоопланктона и перифитона вычисляется по формуле (Pantle, Buck, 1955; Slă
decek, 1973):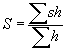 ,
,
где
s — индивидуальная сапробность каждого вида, h — численность вида или относительная частота встречаемости. Биотический индекс для зообентоса находится по методу Ф.Вудивисса (Woodiwiss, 1964; Вудивисс, 1977), согласно которому по мере повышения уровня загрязнения вод происходит упрощение видовой структуры бентоценоза за счет выпадения индикаторных таксонов при достижении предела их толерантности на фоне снижения общего разнообразия организмов, объединенных в так называемые группы Вудивисса. Специальная шкала, учитывающая присутствие показательных организмов и число групп Вудивисса в пробе, позволяет найти искомый биотический индекс. Олигохетный индекс, основанный на увеличении представительности олигохет с ростом уровня загрязнения, рассчитывается как отношение численности видов класса Oligochaeta к общей численности зообентоса (Goodnight, Whitley, 1961).Другой классификатор качества вод предложен С.С.Бариновой (Оценка состояния..., 1992). Он представляет собой 5-балльную шкалу оценок состояния, базирующуюся на объединении нескольких как биологических, так и физико-химических характеристик, в том числе индекса сапробности по Сладечеку, индекса сапробности по Ватанабе, прозрачности воды по диску Секки, содержания хлорофилла, валовой суточной продукции фитопланктона, биомассы фитопланктона, удельной электропроводности воды.
В основе отмеченного индекса Ватанабе (
Watanabe et al., 1986, 1988а,б), как и в случае с индексом Сладечека, лежит анализ сообщества видов-индикаторов сапробности, имеющих свой индикаторный вес. Однако метод разработан только для диатомовых водорослей, представляющих лишь небольшую часть сообществ гидробионтов, что является существенным недостатком метода (Руководство..., 1992).Помимо индексов сапробности, в последнее время чрезвычайно широкое применение при изучении природных сообществ получил индекс видового разнообразия Шеннона, заимствованный из теории информации (
Shannon, Weaver, 1949):![]() ,
,
где
ni — численностьПри всем различии перечисленных индексов их объединяет общий принцип: в основе каждого из них лежит анализ распределения организмов по градиенту загрязнения (в первую очередь, по градиенту органических веществ в воде). При этом какие-либо допустимые пределы для измеряемых переменных не устанавливаются, но вместо этого вводятся экспертные оценки в баллах, значениях сапробности, номера классов качества вод. Естественно, что при практическом использовании такого подхода возникают разнообразные недоразумения, многократно обсуждавшиеся в литературе. В частности нередки случаи, когда оценки полученные по разным биотическим идентификаторам, не совпадают и приходится придумывать методы расчета т.н. интегральных оценок, что порождает “индексы загрязнения“, число которых растет от года к году.
Упомянутые выше показатели объединяет и их общий недостаток: при их построении совершенно игнорируются биотические отношения между популяциями в реальных сообществах, такие как конкуренция, мутуализм и др. Попытка исправить этот недостаток была предпринята В.А.Абакумовым (Абакумов, 1991; Руководство..., 1992). На основе развиваемых им представлений об экологических модификациях предлагается ввести градации состояния экосистем: фоновое состояние, состояние антропогенного экологического напряжения, состояние антропогенного экологического регресса и состояние антропогенного метаболического регресса.
При фоновом состоянии возможны перестройки структуры экосистемы, не ведущие к ее усложнению или упрощению, т.е. не изменяющие общего уровня организации биоценоза (например, смена видов-доминантов, изменение видового состава); не происходит глубоких изменений интенсивности метаболизма биоценоза. Состояние антропогенного экологического напряжения выражается в увеличении разнообразия биоценоза, в уменьшении энтропии, в усложнении межвидовых отношений, в увеличение пространственно-временной гетерогенности, в усложнении пищевой цепи. Состояние антропогенного экологического регресса характеризуется уменьшением видового разнообразия и пространственно-временной гетерогенности, увеличением энтропии, упрощением межвидовых отношений и трофических цепей. О состоянии антропогенного метаболического прогресса свидетельствует увеличение как первичной продукции, так и продукции всех последующих трофических уровней, что сопровождается, как правило, ростом численности и биомассы отдельных компонентов биоценоза. Состояние антропогенного метаболического регресса соответствует снижению активности биоценоза по сумме всех процессов образования и разрушения органического вещества. Этот подход несомненно более “экологичен” и поэтому представляется более обоснованным, чем, скажем, система сапробности или разнообразные биотические индексы, баллы и т.п. Однако и в этом случае мы получаем набор экспертных оценок состояния сообществ, для которых тоже необходимо построение шкал типа "норма-патология".Один из методов применения экологических модификаций основывается на определении изменений интенсивности общего метаболизма биоценоза, оцениваемых через продукционные характеристики фитопланктона (Абакумов, Сиренко, 1988; Сиренко, 1991). В качестве характеристик интенсивности метаболизма используется отношение продукции и деструкции фитопланктона, а также характер вертикального распределения хлорофилла, определяемый по его нативной флуоресценции, в том числе и дистанционными методами анализа.
Ряд исследований посвящён оценке антропогенных экологических модификаций сообщества макрозообентоса (Попченко, 1988, 1991, 1994; Раддэм и др., 1991). Большой вклад в теоретическую и практическую разработку проблемы внесли работы В.И.Попченко, который предлагает оценивать экологические модификации биоценоза через посредство его функциональных характеристик. В качестве таковых предлагается отношение общего дыхания сообществ водных беспозвоночных к его суммарной биомассе, отношение продукции к биомассе, а также отношение продукции к энергии, рассеиваемой популяцией в пространство. Позднее Попченко была разработана и предложена схема общих критериальных тестов инвариантных состояний сообщества зообентоса, рекомендованная общепринятыми методиками (Руководство…, 1992). Схема содержит критерии для выявления экологического и метаболического прогресса и регресса донного сообщества.
Другой способ выявления экологических модификаций для сообщества макрозообентоса — это расчет индекса Раддэма (Раддэм и др., 1991). Группы и виды макрозообентоса распределяют по различным классам в соответствии с их устойчивостью к закислению, причём границы между классами выбраны таким образом, чтобы каждый класс соответствовал определённой экологической модификации.
Применение метода экологических модификаций фитопланктона и зообентоса к данным гидробиологического мониторинга Горьковского водохранилища в 1987-1997 гг. показало (Дмитриева, Обридко, 1999), что в начале периода исследований сообщество фитопланктона находилось в состоянии экологического напряжения, а сообщество макрозообентоса — в состоянии экологического регресса.
Переход от одной модификации к другой регистрировали по данным об изменении видового разнообразия. В дальнейшем наблюдали обращение указанных экологических модификаций, связанное со снижением уровня антропогенной нагрузки.Экологические модификации сообщества перифитона исследовали в работах В.Н.Тальских (1991, 1998). Изменения уровня метаболизма перифитона оценивали при помощи индекса Хорасавы (отношение общего количества организмов, не содержащих хлорофилл, к общему количеству организмов с хлорофиллом), а также индекса относительного обилия продуцентов (отношение обилия продуцентов к сумме обилий консументов и редуцентов).
Ряд вариантов оценки антропогенных экологических модификаций биоценоза по показателям микрозоопланктона был предложен С.В.Креневой (Кренева, Гусева, 1991).
В Ладожском озере, в водоемах Молдавии и Калмыкии, в бассейне Северной Двины, на реках о. Сахалин возникновение метаболического прогресса выявляли по изменению численности и биомассы, а экологического регресса — по изменению числа видов инфузорий и коловраток.М.Б.Иванова (1997) отмечает, что при разработке экологических нормативов для природных экосистем следует исходить из поддержания биологического разнообразия и сохранения структуры и функционирования экосистем.
Автором предложена следующая классификация озер по их экологическому состоянию (по сути совпадающая с сериальными стадиями сукцессии), основанная на степени нарушения природного лимногенеза в результате антропогенных процессов эвтрофирования, ацидификации и загрязнения: 1) озера не подвергаются действию антропогенных факторов, или это воздействие настолько незначительно, что не отражается на функциональных показателях экосистемы; 2) озера испытывают пресс антропогенной нагрузки и находятся в состоянии резистентной устойчивости, т.е. лимногенез не нарушен; 3) озера испытывают локальное во времени антропогенное воздействие, приводящее к изменению функционирования экосистемы, но после его прекращения происходит возвращение к исходному состоянию; 4) при усилении антропогенного воздействия происходит постепенное изменение структурных и функциональных характеристик биоценоза; при прекращении воздействия возможен возврат к прежнему состоянию, хотя это более длительный и затратный процесс; 5) массированное поступление в озеро веществ антропогенного происхождения приводит к изменению типа лимногенеза; на месте старой образуется новая экосистема с другими структурными и функциональными характеристиками и связями (пример — превращение исходно ацидных светловодных озер в высокопродуктивные в результате внесения в них удобрений); 6) при непрекращающемся массированном антропогенном воздействии условия в озере меняются настолько, что его экосистема полностью разрушается; так, вследствие выпадения кислых дождей при pH меньше 3.5 возникают так называемые "мертвые" озера с полным отсутствием жизни; чтобы восстановить такой водоем, необходима кардинальная очистка котловины с удалением всех донных осадков.Для экспертной оценки сообществ речных и морских гидробионтов могут быть использованы видовая структура, показатели развития организмов и особенности их распределения (Engle et al., 1994; Груздева и др., 1996; Weber, Isely, 1997; Деревенская, Мингазова, 1998; Лугаськов и др., 1998; Gorham-Test, 1998; McRae et al., 1998; Sivadasan, Joseph, 1998, Stevenson, 1998).
В частности, состав и разнообразие макрозообентоса значительно различались на участках Мексиканского залива с разным уровнем загрязненности седиментов. Для оценки качества воды залива предложен бентический индекс, включающий индекс Шеннона и сведения об относительном обилии тубифицид и двустворчатых моллюсков (Engle et al., 1994). На основании индекса, отражающего количество таксонов и обилие особей макробеспозвоночных, сделан вывод о хорошем качестве воды в бассейне р. Чаттуга (Weber, Isely, 1997). Видовой состав перифитонных сообществ, в частности, диатомовых водорослей, может служить индикатором целостности экосистем (Stevenson, 1998), которая понимается как "способность экосистемы к поддержанию сбалансированного, приспособленного к внешним условиям сообщества организмов, которое характеризуется видовым составом, разнообразием и функциональной организацией, близкими к тем, которые складываются в естественной, ненарушенной, среде обитания данного региона" (Karr, Dudley, 1981). Свидетельством снижения целостности экосистемы является, например, увеличение доли зеленых нитчаток или цианобактерий (Stevenson, 1998).В основу экспертной классификации речных экосистем по показателям зообентоса может быть положен интегральный индекс экологического состояния по биологическим показателям (Зинченко и др., 2000, Выхристюк и др., 2001), учитывающий такие гидробиологические параметры как численность и биомасса бентоса; число видов в сообществе; видовое разнообразие, оцениваемое по индексу Шеннона; биотический индекс Вудивисса и олигохетный индекс Пареле (Пареле, Астапенок, 1975). Интегральный индекс (ИБС) рассчитывается по формуле:
![]() ,
,
где
Bi — относительная оценка используемых биологических показателей на 4-балльной шкале (табл. 5); Nb — количество отобранных биологических показателей. На основе ИБС и интегрального индекса экологического состояния по химическим показателям вычисляется обобщенный индекс экологического состояния водотока, позволяющий выделить три типа экологического состояния: зону экологического бедствия, зону экологического кризиса, зону относительного экологического благополучия. На основе объединения нескольких биотических индикаторов путем оптимального распознавания образов возможно построение так называемого “обобщенного портрета” исследуемого сообщества организмов, т.е. уравнения оптимальной плоскости, переводящей пространство индикаторных признаков в бинарный вид и, соответственно, разделяющей это пространство на “нормальную” и “патологическую” части (Шитиков и др., 2001).Необходимость интегрального подхода при экспертной оценке состояния водных экосистем признается в работах и других авторов (Баканов, 1999, 2000; Баканов и др., 1998; Балушкина, 1997, 2001). Предлагаемые интегральные оценки основаны на том, что исходные гидробиологические показатели нормируются в некоторой единой шкале, после чего суммируются. Констатируя, что в настоящее время для мониторинга пресноводных водоемов по зообентосу применяется свыше 60 методик оценки состояния экосистем, использующих различные индексы или их функциональные комбинации (Баканов, 2000), А.И.Баканов (1999) предложил методику мониторинга пресных водоемов по важнейшим характеристикам бентосных сообществ с использованием комбинированного индекса загрязнения (КИСС).
Индекс объединяет значения 6 показателей бентосного сообщества (суммарной численности N, суммарной биомассы B, числа видов S, индекса Шеннона H, олигохетного индекса Пареле ОИП и средней сапробности пробы СС, рассчитанной как средневзвешенная сапробность трех первых доминирующих по численности видов). Вначале все наблюдения ранжировали по каждому из 6 показателей (ранг 1 присваивали максимальным значениям N, B, S, H и минимальным значениям ОИП и СС). Каждому показателю придавали определенный "вес". Поскольку СС, как показали данные мониторинга, более тесно связана с загрязнением, ее вес — 2, вес B и ОИП — 1.5, вес N, S и H — 1. Тогда КИСС =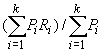 , где Ri — ранг наблюдения по i-му показателю, i — порядковый номер показателя, Pi — "вес" этого показателя, k — число показателей. На 12 станциях Угличского, Рыбинского и Горьковского водохранилищ значения КИСС (9.6-14.4) не отличались от среднего значения (12) больше чем на 0.67δ (δ = 3.6). Οоэтому состояние бентоса здесь характеризовали как удовлетворительное. На 6 станциях руслового участка Волги КИСС был меньше 9.6, что квалифицировано как хорошее состояние. На 5 станциях вблизи Ярославля КИСС превышал 14.4, поэтому оценка состояния здесь была неудовлетворительной, что подтверждалось наблюдением бедного видового состава сообщества, доминированием тубифицид и личинок мотыля Chironomus plumosus.
, где Ri — ранг наблюдения по i-му показателю, i — порядковый номер показателя, Pi — "вес" этого показателя, k — число показателей. На 12 станциях Угличского, Рыбинского и Горьковского водохранилищ значения КИСС (9.6-14.4) не отличались от среднего значения (12) больше чем на 0.67δ (δ = 3.6). Οоэтому состояние бентоса здесь характеризовали как удовлетворительное. На 6 станциях руслового участка Волги КИСС был меньше 9.6, что квалифицировано как хорошее состояние. На 5 станциях вблизи Ярославля КИСС превышал 14.4, поэтому оценка состояния здесь была неудовлетворительной, что подтверждалось наблюдением бедного видового состава сообщества, доминированием тубифицид и личинок мотыля Chironomus plumosus.
Анализ корреляций показал (Балушкина, 2001) положительную связь между интегральным показателем антропогенного воздействия на живые компоненты речной экосистемы (Балушкина, 1997) и большинством измеряемых гидрохимических характеристик воды и донных отложений. На основании значений данного показателя предполагается провести выделение границ классов состояния экосистем.
Примерами биоиндикации для морских акваторий может служить введение интегрального индекса аномальности морской экосистемы, индекса суммарной антропогенной нагрузки, критерия потенциальной экологической опасности (Фащук, 1997).
Напомним, что, кроме конструирования и обоснования самих индексов для целей диагностики, необходим метод отображения множества встречающихся значений индексов на какую-либо разновидность шкалы “норма-патология” для состояний экосистем, например, метод функции желательности, рассмотренный в предыдущем разделе.
4.2. Параметры ранговых распределений
4.2.1. Измерение экологического разнообразия
Огромное разнообразие жизни, пожалуй, — одно из существенных отличий живой материи от косной. Разнообразие можно определить как степень различия объектов в изучаемой совокупности. В разнообразии живого можно выделить эволюционное разнообразие, связанное с различием объектов биосферы в различные периоды ее существования; географическое разнообразие организмов в различных их местообитаниях на Земле; объединяющее первые два – таксономическое разнообразие биологических систематик и другие подходы к разнообразию. Интересующие нас объекты – компоненты экологических сообществ, реально существующие и одновременно сосуществующие в экосистемах.
Измерение разнообразия необходимо, чтобы отслеживать изменения, происходящие в экосистемах; чтобы отличать друг от друга состояния экосистем; чтобы оценивать состояния экосистем на шкале "норма-патология". Задача измерения разнообразия нетривиальна и в первую очередь из-за того, что сообщества — многокомпонентные системы. По одним признакам "выигрывает" одна система, по другим — другая, и требуется способ согласования множества признаков, сосуществующих одновременно.
В самом общем виде удобно рассматривать сообщество как объединение групп различающихся по какому-либо признаку организмов. Это могут быть: популяции биологических видов, размерные группы, возрастные когорты, группы физиологически сходных организмов (например, потребляющих одинаковые ресурсы), группы сходных жизненных форм и т.д.
Наиболее полная информация о количественных характеристиках сообщества содержится в "векторе"
В табл. 7 сведены некоторые из встречающихся в литературе показателей, которые свертывают содержащуюся в векторе
Один из путей в обосновании выбора тех или иных индексов разнообразия предоставляет анализ ранговых распределений численностей видов (Левич, 1980;
Frontier, 1985; Мэгарран, 1992; Пузаченко, Пузаченко, 1996). Ранговое распределение представляет собой преобразованный вектор численностей: наиболее обильной группе присваивается первый номер, следующей по численности группе — второй и так далее до наименее обильной группы, которая имеет номер w, совпадающий с общим числом групп в сообществе. На рис. 10 представлено ранговое распределение численностей видов для приведенного в табл. 6 примера сообщества птиц.Для количественного описания ранговых распределений применяются различные аппроксимации: экспоненциальная модель
n(i) ~ zi, гиперболическая модель n(i) ~ 1/(i+B)b , объединяющая их дзета-модель n(i) ~ zi/(i+B)b , модель "разломанного стержня" n(i) ~ ln1/i (в формулах n(i) обозначает численность особей ранга i; z, b и B — параметры моделей).Известны несколько подходов к обоснованию формы ранговых распределений (Левич, 1996). Например, объяснение экспоненциального закона
(Motomura, 1932) с помощью априорных представлений о различном "могуществе" видов при их взаимодействии в сообществе. Упомянутая выше беспараметрическая модель "разломанного стержня" (MacArthur, 1960) рассчитывает результат случайного бросания точек на отрезок ("стержень"), изображающий доступный сообществу запас единственного и равномерно распределенного ресурса. В.Д.Федоров (1978) в модели "экспоненциально разломанного стержня" делает то же на отрезке с экспоненциально распределенным ресурсом. Р.Кернер (цит. по Песенко, 1978) показал, что логнормальный закон следует из статистической механики системы "хищник — жертва", описываемой уравнениями Вольтерра. Гиперболическую зависимость числа видов с данным значением существенного параметра от величины этого параметра выводят Б.Я.Рябко с соавторами (1978). Адекватная форма ранговых распределений для численностей биологических таксонов на основе модели самоподобных множеств представлена в работе Ю.Г.Пузаченко и А.Ю.Пузаченко (1996).4.2.2. Примеры оценок состояния экосистем по ранговым распределениям
Ранговые распределения могут рассматриваться как инструмент при анализе состояния сообществ (Левич, 1980). Непосредственным объектом анализа при этом может быть форма кривой рангового распределения или при неизменной общей форме — количественные значения его параметров. Ввиду того, что одинаковые значения целостных характеристик сообществ (общая численность, число видов, индексы разнообразия) могут порождаться разными ранговыми распределениями, последние являются более тонким и чувствительным инструментом изучения состояния экосистем.
Метод ранговых распределений применяли для изучения влияния тяжелых металлов на пресноводный планктон (Сироткина, Левич, 1981; Карташева, Левич, 1981). Степень неравномерности распределения численностей видов, которая собственно и характеризуется параметрами ранговых распределений, оказалась существенно подверженной влиянию указанных внешних факторов на сообщество. Так, для фито- и зоопланктона Рыбинского водохранилища уравнения регрессии
, описывающие влияние металлов на показатели биоты, для значений общей численности и числа видов не выявили значимых эффектов влияния, в то время как аналогичные уравнения для ранговых параметров позволили обнаружить воздействия различных добавок загрязнителей.Подобный анализ был проведен при изучении влияния нефтепродуктов, дисперсантов и их комбинаций на фитопланктон Белого моря (Федоров и др., 1977). Было показано, что различные соединения приводят к идентичному изменению численностей, но ранговые распределения вскрывают различное влияние исследованных соединений на структуру сообщества — обнаружены соединения, которые сильнее всех прочих нарушают гиперболичность рангового распределения.
4.2.3. Метод
ABCВ ряде работ оценка состояния экосистемы основывается не на индивидуальных характеристиках рангового распределения биомассы или численности видов, а на сравнении этих распределений. Этот метод был предложен Р.Уорвиком
(Warwick, 1987) для анализа сообществ морского зообентоса и назван им ABC-методом (abundance-biomass comparison method). Он основан на том, что биомасса как носитель консервативной информации медленнее реагирует на изменения среды, а численность — более динамичный показатель реакции сообщества. Поэтому в стабильных сообществах преобладают крупные виды с медленной динамикой, а в нарушенных — мелкие и более динамичные. Если по оси X отложить (в логарифмической шкале) ранги видов порядке уменьшения численности (биомассы), а по оси Y — соответствующие накопленные проценты от общей численности (биомассы), то в стабильных ненарушенных сообществах кривая численности будет лежать ниже кривой биомассы, а в сильно нарушенных сообществах — выше. Состояния неустойчивого равновесия или восстановления сообщества после стресса дают приблизительно совпадающие или пересекающиеся кривые.Для характеристики соотношения ранговых распределений биомассы и численности использовали различные числовые индексы. В одном случае (
Beukema, 1988) вычисляли сумму разностей между накопленными процентами биомассы и численности по всем рангам. В другом (Meire, Dereu, 1990) — усредненную величину этой разности в расчете на один вид. В обоих случаях положительные значения индекса соответствуют нормальным, отрицательные — нарушенным сообществам.ABC-метод с успехом применяли при анализе экологического состояния сообществ морского зообентоса (Аверинцев, Жуков, 1987; Аверинцев, 1991; Warwick, 1987; Meire, Dereu, 1990). Однако метод следует с осторожностью применять в ситуациях, когда в норме преобладают организмы с высокой, но изменчивой численностью, а также в районах с постоянным стрессовым воздействием среды; существенное значение имеют предельные размеры организмов, включаемых в рассмотрение (например, совместное рассмотрение микро- и макроорганизмов может привести к невозможности адекватной интерпретации результатов).
4.2.4. Ранговые распределения в экологии сообществ с точки зрения статистики
Оставаясь весьма эффективным способом оценки состояния природных экосистем, метод ранговых распределений в своем традиционном виде сталкивается с рядом проблем статистического характера (Максимов, 2002).
Первый вопрос возникает уже во время самой процедуры ранжирования — почему 1-й ранг приписывается наиболее обильному виду? Не будет ли более естественным ранжировать виды по возрастанию их обилия, так чтобы наиболее обильный вид получил бы и наибольший ранг. Именно так поступают, кстати, и при построении ранговых статистик.
Впрочем порядок ранжировки может быть и не столь важен. Более существенные вопросы возникают при знакомстве с традиционными методами получения математического описания (модели) рангового распределения. Как уже было сказано выше, на соответствующем графике ранги откладываются по оси абсцисс, а обилия или экологические значимости видов — по оси ординат. В силу сложившейся традиции это означает, что ранг рассматривается, как независимая, а обилие, как зависимая переменная. Поэтому и уравнения, используемые для аппроксимации эмпирической связи, имеют вид
ni = f(i). Между тем, если подумать, то по самому способу получения ранжированного ряда ранг определяется исследователем в зависимости от обилия и, как это ни парадоксально на первый взгляд, с изрядной долей произвола. Произвол этот заключается не только в порядке ранжирования (по возрастанию или по убыванию), и в использовании дробных рангов или иных способов построения балльных шкал, но в первую очередь в самой процедуре ранжировки. Смысл последнего утверждения проще всего продемонстрировать на простом примере.получим с помощью генератора случайных чисел 5 таких чисел, распределенных по Пуассону, скажем, 43, 49, 54, 38, 43, ранжируем их в порядке убывания:
|
ранг i |
1 |
2 |
3 |
4 |
5 |
|
число n i |
54 |
49 |
44 |
43 |
38 |
и построим график в полном соответствии с вышеописанной методикой (рис. 11).
Поскольку полученные точки совершенно идеально "ложатся на прямую"
ln(ni) = 4.0628 - 0.0833i с коэффициентом детерминации R2 = 0.972, были бы все основания объявить полученный ряд чисел геометрическим рядом со всеми сопровождающими "экологическими" рассуждениями о последовательном использовании ресурса с постоянной долей изъятия и т.п., если бы эти числа были оценками обилия каких-то видов в какой-то экосистеме. А то, что такое возможно, нетрудно увидеть в другом, столь же простом, примере:|
ранг |
1 |
2 |
3 |
4 |
5 |
|
численность птиц |
115 |
103 |
92 |
67 |
65 |
Эти данные взяты из примера, иллюстрирующего распределение обилий птиц, из табл. 6 (Мэгарран, 1992). И здесь график в тех же координатах
(рис. 12) выглядит не менее идеально (коэффициент детерминации для уравнения ln(ni) = 4.9274 - 0.1571i практически такой же — 0.941). Но где гарантия, что найденная "зависимость" действительно отражает некие межвидовые отношения в сообществе, а не является, как в предыдущем примере, простым артефактом ранжировки? Между прочим, проверка по критерию Пирсона ("хи-квадрат") не обнаруживает значимого отличия распределения численности выбранных 5 видов птиц от распределения Пуассона. Известно, что для величины hi = 2Итак, мы сталкиваемся с проблемой: поскольку любая оценка обилия вида в экосистеме, как всякая выборочная оценка, есть величина случайная, а ранжировка этих оценок всегда приводит к получению некоторой монотонной последовательности чисел (не важно, линейной или нелинейной), нужно каким-то образом выделить в этой последовательности случайную составляющую (артефакт ранжировки — ранжировка ошибок определения обилия). Возможно, что среди специалистов по прикладному регрессионному анализу этот вопрос и обсуждался, но мы не встречали в доступной мне литературе следов такого обсуждения.
Еще один вопрос возникает по поводу правомерности использования регрессионного анализа для получения уравнения связи между обилием вида и его рангом . Общеизвестны требования к переменным, предусмотренные теорией регрессионного анализа — см. например, книгу Н.Дрейпера и Г.Смита (1986). Одно из этих требований заключается в том, что независимая переменная должна быть детерминированной и непрерывной величиной. Между тем ранги на оси абсцисс на рис. 11 и 12 — дискретны. Это значит, что на этой оси не может быть точки с абсциссой, скажем 1.2 или 4.65, а следовательно и прямые, практически идеально проведенные через совокупность экспериментальных точек, являются по сути своей чистой фикцией: реальный смысл на них имеют только точки с абсциссами, равными целым числам. Справедливости ради следует заметить, что в огромном большинстве случаев, когда регрессионный анализ применяют к реальным экспериментальным данным — в особенности в экологических исследованиях — теоретические требования к переменным не выполняются. Об этом неоднократно говорилось в различных руководствах по прикладной статистике и, пожалуй, наиболее четко — в предисловии переводчиков, Ю.П.Адлера и В.Г.Горского, к русскому переводу вышеупомянутой книги Дрейпера и Смита.
Вернемся вновь к примеру с сообществом птиц (табл. 6). Число 115 — это численность попугаев розелла, 103 — численность попугаев какаду, 92 — численность белобрюхих медососов. Расположив эти числа в убывающий ряд и приписав им разные ранги, можно утверждать, что обилие розелл в австралийском жестколистном лесу превышало обилие какаду, которых в свою очередь было больше, чем белобрюхих медососов. Однако в реальности очень трудно согласиться с таким категорическим утверждением. Гораздо более правдоподобным было бы утверждение, что обилие всех 3-х видов примерно одинаково. Но тогда этим видам следует приписать один и тот же ранг. Далее в ранжированном ряду находятся еще 2 вида, которые мало отличаются друг от друга по численности, так что им также следовало бы приписать один и тот же ранг. Возникает вопрос, какова величина этих объединенных рангов
? В практике применения ранговых статистик принято одинаковым числам в ранжированном ряду приписывать некоторые средние ранги. Тогда первые три вида в нашем примере получат ранг, равный 2, виды 4-й и 5-й — ранг, равный 4.5. Отсюда следует, что не численность зависит от ранга, а ранг зависит от численности и к тому же именно численность, как независимая переменная, при общепринятой процедуре ранжировки оказывается строго детерминированной величиной, а ранг, как зависимая переменная, определяется с погрешностью.Поясним это на том же примере. Откуда взялись числа 115 и 103, которым были приписаны ранги 1 и 2? Неизвестно, каким именно способом оценивалось обилие птиц в лесу, но допустим, что это просто число розелл и какаду, которых увидел исследователь, двигаясь, например, по некоторому маршруту в австралийском влажном жестколистном лесу. Это не значит, конечно, что их было на этом маршруте в точности 115 и 103, но увидел-то он именно 115 розелл, а не 114 и не 116. И если в действительности в лесу какаду было больше, чем розелл, и орнитолог совершенно случайно увидел их всего 103, а не 116 или 120, то ошибка в определении обилия выразится как раз в том, что розеллы получили 1-й ранг, а какаду - 2-й.
Итак, если согласиться с вышеприведенными рассуждениями, то график рангового распределения следует строить, откладывая численности по оси абсцисс, а ранги — по оси ординат. Получаем рис. 13, на котором представлены те же данные, но теперь численностям приписаны ранги по возрастанию, по оси абсцисс отложены численности, а по оси ординат — ранги. Понятно, что зависимость ранга от численности не отличается от линейной. Уравнение
i = 0.07 ni -3.20 описывает эту зависимость с коэффициентом детерминации R2 = 0.954, тем же, что для прямой на рис. 12.Для сравнения на этом же рисунке проведены кривые i = 5.992ln(
ni) - 23.7 с коэффициентом детерминации R2 = 0.941 и i = 8·10-5ni2.328, для которого R2 = 0.880. Первое из них линеаризуется при логарифмировании численностей (по оси абсцисс), а второе - при логарифмировании и численностей и рангов. Кстати, если логарифмирование численностей и может иметь какой-то биологический или хотя бы статистический смысл, то логарифмирование рангов совершенно неоправданно ни с точки зрения экологии, ни с точки зрения статистики. Важно, однако, что различия в коэффициентах детерминации для всех 3-х уравнений совершенно несущественны, иными словами нелинейные зависимости (по крайней мере по такому показателю качества аппроксимации, как R2) ничем не лучше простого линейного уравнения.Теперь посмотрим, что получится, если для примера из книги Э.Мэгарран построить график зависимости ранга от численности, пронумеровав все виды, представленные в списке, от 1-го до 31-го в порядке возрастания их обилия (рис. 14). Очевидно, что все точки на графике четко разделяются на две совокупности, каждая из которых практически идеально ложится на прямую. Только для видов, представленных в списке менее чем 10 особями, прямая описывается уравнением
i = 1.727ni + 0.4, а для остальных — i = 0.126ni + 17.78. Ранжируя по обилию виды, представленные в списке численностями от 1 до 9, мы по сути ранжируем погрешности в их подсчете. Отсюда вряд ли оправданно делать вывод о том, что, например экологическая ниша вьюрка имеет больший объем, чем у лирохвоста, на том основании, что в списке значится 6 вьюрков и 2 лирохвоста. Если же рассчитать величину χ2 для первых 16 видов (численность которых меньше 10) в предположении, что они распределены по Пуассону, то получим величину 27.20, лишь немного превышающую критическое значение при 5%-м уровне (25.00) и меньшую, чем при 1%-м уровне (30.58). Т. е. распределение численностей 16 наименее обильных видов птиц практически не отличается от совершенно случайного и, скорее всего, не свидетельствует о наличии каких-либо экологических взаимодействий между ними.Еще один вопрос, возникающий при построении ранговых распределений — почему вместо численностей обычно используют их логарифмы? Чаще всего это объясняют соображениями удобства: поскольку обильные виды обычно присутствуют в пробе в количествах, измеряемых десятками, а то и сотнями, а редкие виды представлены одной-двумя особями, логарифмирование позволяет расположить соответствующие точки на оси более равномерно и график получается более наглядным. В частности на таком графике
якобы сразу можно увидеть, подчиняется ли распределение экспоненциальному закону. Однако, эти объяснения кажутся малоубедительными. Предшествующий опыт аппроксимации эмпирических зависимостей уравнениями регрессии показал, что начинать надо с линейной модели и только после того, как статистическая проверка покажет, что эта простейшая модель неадэкватна, имеет смысл заниматься поиском нелинейной функции, более подходящей для описания экспериментальных данных.Выбранный здесь пример позволяет продемонстрировать и некоторые неблагоприятные последствия подобной операции. На рис. 15 изображен именно такой традиционный график по тем же данным, что и на рис. 14, где по оси абсцисс отложены ранги видов по убыванию, а по оси ординат — логарифмы численностей. Прямая
ln(ni) = 4.918 - 0.153i описывает экспериментальные данные с коэффициентом детерминации R2 = 0.986. Никаких изломов на этом графике не видно и, если ограничиться лишь таким поверхностным анализом, можно заключить, что распределение птиц подчиняется модели Мотомуры со всеми экологическими выводами, следующими из толкования этой модели, предложенного Р.Уиттекером (1980).При более внимательном рассмотрении рис. 15 можно заметить, что экспериментальные точки располагаются около “теоретической прямой” несколько волнообразно. Особенно хорошо это видно, если воспользоваться приемом, рекомендованным В.Н.Тутубалиным: надо поднять лист с рисунком на уровень глаз, держа его горизонтально, и смотреть вдоль линии регрессии. Две “полуволны”, соответствующие двум совокупностям точек на рассмотренном ранее рис. 14, становятся при этом отчетливо видны, а разделяют их как раз 15-й и 16-й виды, т.е. виды с числом особей больше 10 и меньше 10. Естественно, точно такая же картина получится и в том случае, если мы пронумеруем виды в порядке возрастания и построим график зависимости ранга от логарифма численности.
Более строгую проверку предположения о существовании двух "полуволн" можно осуществить, если воспользоваться приемом, предусмотренным стандартной процедурой линейного регрессионного анализа и называемым “анализом остатков”. На рис. 16 величины остатков (т.е. разностей между экспериментальными значениями
ln(ni) и и величинами, предсказываемыми уравнением ln(ni) = 4.918 - 0.153i) отложены на оси ординат, а на оси абсцисс отложены соответствующие им предсказанные значения ln(ni). На этом графике уже совершенно четко можно увидеть 2 положительных “полуволны” остатков, а наибольший по абсолютной величине отрицательный остаток приходится примерно на величину ni = 12.При анализе остатков качество аппроксимации, проверяют обычно с помощью критерия Дарбина-Уотсона
D. Этот показатель более надежен, чем коэффициент детерминации. По критерию Дарбина-Уотсона проверяется наличие корреляции остатков, которой не должно быть, если прямая линия удовлетворительно описывает экспериментальные данные. В нашем примере D = 0.912, а для однофакторной зависимости и 31 экспериментальной точки она должна быть не меньше 1.36 (нижнее табличное значение этого критерия при 5%-м уровне значимости). Таким образом приходится отбросить гипотезу о статистической независимости остатков и признать, что они существенно скоррелированы. В этом убеждает и величина сериального коэффициента корреляции: rs = 0.539, значимо отличная от 0. Но отсюда следует, что прямая на рис. 15 не так уж хорошо описывает экспериментальные данные, как это кажется на первый взгляд.Итак, можно резюмировать, что логарифмирование численностей в данном примере лишь создает иллюзию простой линейной связи логарифмов численности и их рангов и затушевывает наличие более сложной зависимости, ясно видной на рис. 14. Но если распределение численности 16 наименее обильных видов совершенно случайно, то по-видимому имеет смысл исследовать закономерность распределения видов по обилию только для остальных 15 видов, численность которых в обсуждаемом списке превышает 10 особей. Анализ остатков и в этом случае показывает, что несмотря на высоко значимую величину коэффициента детерминации
R2 = 0.945 вряд ли можно удовлетвориться простой линейной зависимостью ранга от численности, так как D = 0.709, и rs = 0.553, ясно показывают существенную скоррелированность остатков. не спасает и логарифмирование численностей, которое приводит к незначительному снижению этой скоррелированности (D = 0.923; rs = 0.480). в этом легко убедиться, посмотрев на рис. 17а,б , где представлены графики для остатков против предсказанных значений рангов, как для исходных значений численностей (рис. 17а), так и для их логарифмов (рис. 17б).На рис. 18 приведен еще один график остатков, полученных для линейной зависимости рангов от квадратных корней численности. Соответствующие значения критерия Дарбина-Уотсона и сериального коэффициента корреляции (
D = 2.007; rs = -0.043) не дают никаких оснований утверждать, что остатки скоррелированы, и в этом смысле линейная зависимость ранга от квадратного корня из численности явно лучше, чем зависимость от численности или от логарифма численности, хотя коэффициенты детерминации во всех этих вариантах принципиально не отличаются (0.945 для численности, 0.971 для логарифма и 0.986 для квадратного корня).Извлечение квадратного корня рекомендуется как более предпочтительное преобразование переменных, чем логарифмирование, хотя бы потому, что не возникает проблемы с нулями. Когда речь идет о количестве особей, подсчитанных в пробе, отобранной тем или иным способом, важно также, что не менее традиционным, чем логарифмирование, является у экологов представление о том, что погрешность счета определяется, как квадратный корень из числа обнаруженных особей, т.е
. в предположении, что в пространстве, откуда взята проба, особи были распределены по закону Пуассона. Характерно, однако, что и в основе разнообразных моделей, придуманных для описания пространственного распределения особей, лежит именно закон Пуассона. Поэтому извлечение квадратного корня из численностей в какой-то мере можно трактовать, как стандартизацию переменной. Иными словами, обилие вида в пробе измеряется в этом случае не штуками, а стандартными отклонениями счета. Конечно эта трактовка не претендует на то, чтобы быть единственно правильной, но она по крайней мере более осмыслена, чем логарифмирование численностей, а тем более логарифмирование рангов.Таким образом, изучение зависимости распределения видов по обилию наиболее разумно, по-видимому, начинать с построения графика, на котором по оси абсцисс откладывают численности видов в пробе, а по оси ординат — их номера в порядке возрастания (ранги) и, прежде чем искать некую модель для описания искомой зависимости, следует проверить гипотезу о том, что численности наименее обильных видов распределены по Пуассону. Только после этого имеет смысл подгонять данные о распределении обилия остальных видов под некоторую теоретическую модель.
Посмотрим теперь на график на рис. 14 с несколько иной точки зрения. Что представляют собой ранги видов на оси ординат? Если отвлечься от экологического содержания, скрывающегося за числами на оси абсцисс, то величины рангов — это просто накопленные частоты в ряду этих чисел и можно рассчитать вероятности нахождения каждого из них левее (т.е. меньше) заданного (например, по формуле
pi = (i - 0.5)/w) в предположении, что мы имеем дело с выборкой w чисел из нормально распределенной генеральной совокупности). Тогда вместо рис. 14 получим график эмпирической функции распределения численностей, а для проверки соответствия этого распределения какому-либо теоретическому закону следует выбрать для оси ординат масштаб, соответствующий этому закону, и убедиться, что при этом эмпирический график спрямляется.При подгонке эмпирического распределения под какую-либо другую модель даже в самых современных версиях статистических программ (например 6-й версии STATISTICA или 7-й версии SYSTAT) предлагается использовать традиционные частотные распределения вместо ранговых. Недостаток этого подхода заключается прежде всего в том, что для определения частот необходимо разбить весь набор численностей на классы, с тем чтобы подсчитать число видов (частоту), попавших в каждый класс. При этом, если разбиение осуществляется по линейной шкале, то из-за неравномерности распределения численностей большое количество классов оказываются малочисленными или вообще пустыми и тогда обычные статистические проверки требуют объединения классов, в каждом конкретном случае — совершенно произвольного. Поэтому, опять
-таки в силу сложившихся традиций, разбиение на классы производят по логарифмической шкале. Чаще всего, следуя Престону (Preston, 1948), разбивают численности по удвоению, т.е. назначая верхние границы классов, как 2n: 2, 4, 8, 16 и т.д. В книге Э.Мэгарран приводятся примеры с разбиением на классы по утроению (т.е. на основе троичных логарифмов) и по десятичной логарифмической шкале.Таким образом, при построении частотных распределений в отличие от ранговых мы допускаем двойной произвол: выбор числа классов и выбор способа разбиения. То, что от этого произвола вид получаемых гистограмм может меняться довольно существенно, давно и хорошо известно. В частности именно поэтому Г.Хан и С.Шапиро в своей книге “Статистические модели в инженерных задачах” (1969) рекомендовали использовать полувероятностные графики вместо построения обманчиво наглядных гистограмм при выборе теоретического закона распределения, адекватного экспериментальным данным. К какой путанице и разногласиям приводит следование традиции при описании видовой структуры сообществ, легко увидеть в вышеупомянутой книге Э.Мэгарран в разделе, посвященном логарифмически нормальному распределению (стр.25-35).
К тому, что там написано, можно добавить еще одно соображение. До знакомства с книгой Г.Хана и С.Шапиро мы считали, что более или менее надежная оценка соответствия эмпирических данных теоретическому закону, основанная на сравнении частотных распределений по критерию Пирсона (χ
2), возможна только, если выборка достаточно велика — как минимум 50, а лучше — больше 100 реализаций. Это значит, что описание видовой структуры каким-либо частотным распределением имеет смысл искать, если в пробе обнаружено не менее 50 видов.Между тем в нашей многолетней практике исследования сообществ планктона и перифитона лишь однажды мы имели дело с такой выборкой. Во время экспедиции в Ледовитом океане была отобрана 51 проба, по 1 л каждая, в одном и том месте (пролив Вилькицкого), в одно и то же время. Во всех этих пробах Н.Е.Лихачева подсчитала численность видов и затем этот уникальный материал был использован для проверки различных свойств рангового распределения видов (Лихачева и др. 1979). в пробе, сконцентрированной из 51 литра, после подсчета более 20000 клеток водорослей было обнаружено всего 95 видов. Обычно же, как известно, в планктонных пробах число обнаруженных видов фитопланктона редко бывает больше 30, а видов зоопланктона (со всеми личиночными стадиями) — больше 20.
Тут сразу же конечно возникает вопрос о репрезентативности таких “обычных” планктонных проб. Флористические и фаунистические списки планктонных видов даже для небольших северных озер содержат сотни наименований видов и разновидностей, которые к тому же постоянно пополняются после каждого нового обследования. Ясно, что в каждую пробу, взятую по общепринятым методикам, попадают далеко не все виды, обитающие в данном месте. Да и в рассмотренном выше примере с австралийскими птицами вряд ли список, содержащий 31 вид, полностью представляет орнитофауну влажного жестколистного леса Австралии. Впрочем все полевые экологи прекрасно отдают себе в этом отчет и понимают, что любая, даже очень тщательно отобранная и обработанная проба нерепрезентативна в строгом смысле, но тем не менее дает полезную информацию хотя бы о видах, наиболее обильных для данного местообитания.
Возвращаясь к сообществу птиц, зададимся вопросом: на сколько классов следует разбить их численности? Известна формула, по которой число классов
k = 1.44lnW +1, где W — объем выборки (в данном случае это число видов в пробе). Для 31 вида получаем, следовательно, 6 классов. Если разбивать данную совокупность на вышеупомянутые “октавы”, то верхние границы классов получатся такими: 1, 2, 4, 8, 16, 32. Такое разбиение явно не годится для данной совокупности, так как 10 видов с численностями, превышающими 32, не попадут ни в один из классов. Придется добавить еще 2 класса с верхними границами 64 и 128 и тогда получим таблицу 1.Значение χ
2 для такого разбиения на классы равно 13.65, что для 7 степеней свободы соответствует вероятности по распределению Пирсона, равной 0.0578, т.е. превышает 5%-й уровень значимости. (Считается, что 1-я модель Мак-Артура не имеет параметров, поэтому число степеней свободы для χ2 на 1 меньше числа классов). Таким образом нет достаточных оснований отвергать гипотезу о том, что распределение численности птиц отличается от модели разломанного стержня.В любом популярном руководстве по биометрии или по прикладной статистике можно однако найти никак не обоснованную рекомендацию, согласно которой следует объединять соседние классы, если в каком-нибудь из них частота меньше 5. Посмотрим, что получится, если по этой рекомендации объединить первые 3 класса и 5-й класс с 6-м. Сравнение частот с предсказанием модели представлено в той же табл. 8, а χ
2 в этом случае оказывается равным 11.62. Но для 4 степеней свободы эта величина дает вероятность 0.0204, т.е. меньше, чем 0.05, но больше, чем 0.01. Это как раз тот случай, о котором в тех же популярных руководствах пишут, как о неопределенной ситуации, когда для отбрасывания 0-гипотезы все-таки нет достаточных оснований, но и принимать ее без всяких оговорок не следует.Впрочем, как в этом, так и в предыдущем варианте, статистик предпочитает сформулировать вывод еще более уклончиво: объем материала недостаточен для того, чтобы отбросить 0-гипотезу, а вопрос о том, можно ли принять эту гипотезу, остается на совести исследователя. Мы, таким образом, приходим к тому, с чего начали: совокупность из 31 числа слишком мала, чтобы с помощью критерия Пирсона можно было уверенно оценить ее соответствие некоторому теоретическому распределению.
Разобьем теперь те же численности не по удвоению, а по утроению (назовем эти классы терциями по аналогии с октавами). Получим табл. 9. заметим, что при таком разбиении получается как раз 6 классов.
Величина χ
2 для исходного разбиения равна 12.35, что для 5 степеней свободы соответствует вероятности 0.0303. Мы опять оказываемся в неопределенной ситуации, что конечно неудивительно, поскольку объем выборки остался прежним, но при разбиении на октавы вероятность была 0.0578. т.е. больше 0.05. Если же объединить классы, чтобы их наполнение было не меньше 5, то вероятность по критерию Пирсона, равная 0.0197, оказывается еще ближе к 1%-му уровню. Получается, что при разбиении на октавы 1-я модель Мак-Артура была приемлемой, а при разбиении на терции в ее справедливости появляются определенные сомнения.При внимательном рассмотрении табл. 8 и 9 обращает на себя внимание и еще одно обстоятельство. В таблице 8 в классе обилий от 17 до 32 особей реально было обнаружено всего 2 вида, тогда как по модели их должно было быть не меньше 7. В табл. 9 в классе от 10 до 27 особей реально наблюдалось вдвое меньше видов (5), чем предсказано по модели (10.6). Поскольку речь идет о достаточно многочисленных видах, трудно представить себе, что орнитолог мог не заметить 5-6 видов, численность которых на исследованном участке леса составляет от 1 до 3 десятков. Но если в табл. 9 этот “недоучет” можно “списать” на то, что в предыдущем классе (от 4 до 9 особей) оказалось как раз на 5 видов больше, чем предсказано, то в табл. 8 число видов в обоих соседних классах, пусть на 1-2, но тоже меньше, чем должно быть по модели. И опять получается, что результат анализа зависит от способа разбиения на классы одних и тех же данных.
Приведенные соображения совершенно очевидны для профессиональных статистиков и не нуждаются в столь подробных объяснениях. Но для экологов, в особенности тех, кто использует стандартные компьютерные программы, было бы полезно, как нам кажется, убедиться, что наглядность столь популярных гистограмм распределений может оказаться весьма обманчивой, а критерий Пирсона — далеко не лучший показатель для оценки соответствия теоретического и эмпирического распределения.
Прежде чем ответить на вопрос, для чего нужны модели ранговых распределений, можно еще раз упомянуть ту исходную идею, что характер распределения видов по обилию отражает историю данного сообщества и определяется всей совокупностью взаимоотношений составляющих его видов. Поскольку опять-таки в силу традиции среди этих взаимоотношений самыми важными считаются конкурентные отношения, то численное преобладание одного или немногих видов должно свидетельствовать о том, что именно они являются победителями в борьбе за использование некоего ресурса, лимитирующего рост численности всего сообщества. Отсюда и возникают упомянутые выше трактовки экспоненциальной модели, которая свидетельствует о постоянстве доли доступного ресурса у всех участников конкуренции, а также модели Мак-Артура.
Вряд ли стоит подробно обсуждать противоречивость и малую обоснованность представления о том, что обилие вида в данный момент времени (когда отобрана проба и произведен учет численности) однозначно соответствует количеству использованного ресурса. Может быть это в какой-то степени верно для равновесного — климаксного — сообщества и даже не для сообщества в полном смысле этого слова, а лишь для гильдии или в крайнем случае для таксоцена в составе климаксного сообщества. Если же мы имеем дело с экосистемами на той или иной сериальной стадии, то ни о каком подобном соответствии не может быть и речи.
Может быть это утверждение и выглядит слишком категорическим и голословным, но если оно неверно, то не кажется ли странным, что вот уже почти полвека из одного учебника экологии в другой переходят одни и те же примеры, приводимые в пользу именно этого соответствия? Впрочем в пользу такого утверждения можно привести и некоторое подобие “доказательства от противного”. Действительно, допустим, что мы обнаружили, что в некотором сообществе численность видов распределена по геометрическому ряду, и мы делаем вывод, что имеется некий ресурс, потребление которого уменьшается от вида к виду в той же пропорции, что и обилие. Хорошо известно, однако, что даже если обилие видов в некоем списке описывается вполне удовлетворительно некоторой моделью, это вовсе не означает, что виды, попавшие в этот список, взаимодействуют именно так, как это предполагалось при построении данной модели. На это еще в 1968 году обращал внимание экологов Дж. Коэн, о чем недавно напомнил П. Морин в своем учебнике “Экология сообществ”, изданном в 1999 г. (Morin,1999).
Итак, чтобы убедиться в том, что в соответствии с моделью геометрического ряда лимитирующий ресурс был действительно использован в порядке убывающей геометрической прогрессии, нужно во-первых установить, что это за ресурс — количество пищи (и какой именно), объем занимаемого пространства, число убежищ и т.д.. Далее надо убедиться, что у каждого вида экономический коэффициент, т.е. прирост численности на единицу потребленного ресурса, один и тот же. Вдобавок к этому надо бы еще выяснить, насколько одинаково все исследованные виды выедаются хищниками. Если все эти условия выполнены, можно было бы не сомневаться в применимости модели Мотомуры к реальной экологической ситуации. Но нам не удалось обнаружить ссылок на работы, где подобная проверка адекватности модели рангового распределения была бы проведена.
Другая идея, оправдывающая интерес экологов к ранговым распределениям, сводится к тому, что вид этих распределений некоторым образом может быть связан с такой популярной характеристикой сообщества, как видовое разнообразие. Эта связь достаточно подробно была исследована А.П.Левичем (Левич, 1980; Levich, 2000). Было показано, что некоторые индексы разнообразия прямо связаны с параметрами ранговых распределений. После этого ничего принципиально нового в данном направлении сделано не было и можно лишь отметить, что в большинстве работ, в которых использовались индексы разнообразия, при выборе того или иного индекса вид рангового распределения во внимание не принимался. Единственно о чем стоит упомянуть — это пожалуй то, что все множество индексов разделяют теперь на собственно индексы разнообразия, которые в основном определяются числом видов и в меньшей степени зависят от характера распределения видов по обилию, и на индексы выровненности, величина которых как раз в первую очередь зависит именно от того, насколько равномерно распределены численности видов в изучаемом сообществе.
Надо сказать, что в последние годы интерес к индексам разнообразия со стороны экологов-теоретиков значительно снизился, но зато он сохраняется среди прикладных экологов, озабоченных поиском так называемых интегральных показателей состояния сообществ, которые могли бы служить оценкой антропогенного воздействия (прежде всего, загрязнений) на экосистемы. И в этом случае сохраняется надежда, что для решения такой задачи могут оказаться полезными разнообразные свойства ранговых распределений. Основания для таких надежд заключаются естественно в том, что, влияя на жизнедеятельность
видов, составляющих сообщество, загрязнения могут существенно изменять и характер их экологических взаимодействий, что должно отражаться и на характере распределения видов по обилию.Если согласиться с тем, что ранговые распределения в их традиционной форме являются по сути обычными эмпирическими функциями распределения, только построенными, так сказать, “задом-наперед”, то возникает вопрос: нужно ли изобретать для их аппроксимации какие-то новые модели в дополнение к огромному множеству уже известных теоретических распределений? А если нужно просто свернуть информацию, содержащуюся в списке видов с их обилиями, до одной-двух цифр, то можно, как нам кажется, воспользоваться давно известными параметрами, основанными на оценках статистических моментов. Как было сказано в разделе 4.1 индекс Шеннона по сути не дает никакой новой информации о распределении обилий видов по сравнению с обычными статистическими показателями — коэффициентом вариации и асимметрией (Воробейчик, 1994). Довольно большой эмпирический материал, накопленный нами, позволяет говорить, что между этим индексом и коэффициентом вариации действительно обнаруживается, хотя и нелинейная, но вполне отчетливая связь. Не менее четкая связь существует и между индексом выровненности Пиелу и коэффициентом асимметрии. Остается пока открытым вопрос: может ли дать что-нибудь принципиально новое для оценки состояния сообщества рассмотрение собственно графиков рангового распределения, как неких “паттернов”, о чем неоднократно говорил В.В.Налимов.
Указанные особенности построения моделей ранговых распределений следует учитывать при их использовании для биотической оценки последствий нарушающих воздействий на экосистему. Ведь адекватно оценивая распределение видов в сообществе по обилию, можно своевременно фиксировать изменения характера их экологических взаимодействий, которые, в свою очередь, являются следствием загрязнений и других антропогенных и природных нагрузок.
4.3. Эталонные экосистемы
Идея использования эталонных экосистем с самого начала была в основе системы экологического мониторинга (см. например: Израэль, 1984). В дальнейшем она была практически осуществлена в виде программы фонового мониторинга, как одного из элементов государственного контроля состояния природной среды. Очевидно, что, проводя систематические наблюдения за изменениями абиотических (физико-химических) условий в заповедниках или на территориях, достаточно удаленных от крупных промышленных центров и не подверженных интенсивному антропогенному воздействию, можно получить представление о тех естественных колебаниях абиотических факторов, которые не приводят к каким-либо нарушениям экологических процессов в соответствующих биоценозах.
Неясно, однако, насколько по этим естественным колебаниям можно судить о допустимых или предельных уровнях изучаемых абиотических факторов. Надо еще учесть, что при всех очевидных отличиях экосистем от организмов у них есть одно несомненное сходство: каждая из этих биологических систем по-своему уникальна. Поэтому, если даже в ходе многолетних наблюдений, проведенных, скажем, на заповедном озере Ильмень, мы установим допустимые пределы для содержания биогенных элементов, тяжелых металлов и т.п. в его водах, вряд ли эти "нормы" можно будет рекомендовать для природоохранных организаций Новгородской области, озабоченных состоянием экосистем других озер региона.
Заметим также, что такой подход по сути мало отличается от вышеупомянутых экспертных оценок. Исходная предпосылка здесь все-таки "химическая" — эталонные экосистемы выбираются не столько на основе оценки их стабильности или, если угодно, полноценности, как биологических систем, сколько по тем соображениям, что ввиду отсутствия интенсивного антропогенного воздействия уровень загрязнений в них не должен быть слишком высок (о полном отсутствии таковых, к сожалению, говорить уже не приходится).
Поэтому более обоснованным представляется выделение эталонных участков в пределах каждой конкретной экосистемы или в каждом конкретном водоеме. Поскольку любые изменения в уровнях абиотических факторов вызывают структурные изменения (т.е. изменения видового состава) в сообществе, то критерием для такого выделения должно быть относительное постоянство видовой структуры в пределах эталонного участка. Это постоянство можно оценивать, измеряя сходство видового состава в пробах, собранных на станциях экологического мониторинга. Например, при оценке сходства планктонных и перифитонных сообществ, как биотических идентификаторов, предлагается использовать индекс сходства, основанный на ранжировании по обилию наиболее многочисленных видов в пробах (Максимов, 1991б). Пространственная изменчивость абиотических факторов в пробах, взятых на эталонном участке, должна, очевидно, характеризовать такие изменения этих факторов, которые можно считать несущественными в их влиянии на эталонное сообщество.
Измеряя сходство видового состава сообщества на тех же станциях в течение ряда лет, можно выделить группу станций, на которых видовая структура остается стабильной не только в пространстве, но и во времени. Иначе говоря, на данном участке водоема изменения видового состава, даже если они и значительны, например, вследствие смены сезонных комплексов, должны воспроизводиться от года к году, т.е. быть обратимыми. В сущности пространственная и временная стабильность биотических идентификаторов (индикаторных сообществ) и служит основным признаком толерантности данной экосистемы к изменениям внешних условий. Тогда за норму для биологической структуры сообщества могут быть приняты пределы изменений обилия составляющих его видов в пробах, взятых на эталонном участке, а колебания измеряемых абиотических факторов можно считать экологически допустимыми уровнями для данной экосистемы.
4.4. Показатели эффективности функционирования экосистем
Достаточно распространены способы оценки состояния экосистем по структурным, продукционным показателям отдельных компонентов биоты. При этом для наиболее адекватной оценки необходимо сначала определить, что нужно защищать от предполагаемых внешних воздействий, а именно эти цели не всегда четко сформулированы (Calow, 1998). По одним представлениям, региональные (и тем более глобальные) оценки состояния и вычисленные на их основе нормативы воздействий являются слишком общими и отнюдь не универсальными. С этой точки зрения более перспективной является целенаправленная точечная оценка. Вообще изучение всего биоценоза в целом мало реально из-за большого объема работы, поэтому рекомендуется выбрать одну или несколько индикаторных групп (таксономических или функциональных) и изучать необходимые параметры внутри нее (Halffter, 1998). Требуется, чтобы такая группа удовлетворяла некоторым критериям — она должна быть богата легко определяемыми видами; отбор проб не должен наносить ущерба природным комплексам; изменение разнообразия в группе должно коррелировать с изменением разнообразия сообщества в целом. Однако существует и другая точка зрения, заключающаяся в том, что оценка качества среды производится в отношении здоровья всей экосистемы в целом путем интегрирования показателей здоровья ее компонентов, представленных разными видами живых существ (Захаров, Кларк, 1993;
Spang, 1996; Захаров, 2000).Рассмотрим некоторые конкретные показатели эффективности, которые авторы соответствующих работ предлагают использовать при оценке экологического состояния.
Для оценки возможного влияния гидрохимических, гидрологических, климатических характеристик водоема на ихтиофауну была использована многолетняя динамика уловов и урожайности некоторых рыб бассейна р. Дон (Булгаков и др., 1995). Анализировали уловы леща, чехони и судака совместно с бершом
в четырех водохранилищах: Цимлянском, Веселовском, Пролетарском и Усть-Манычском и урожайность сеголеток полупроходного леща и годовиков проходного осетра в нижнем течении Дона.При помощи метода экологически допустимых уровней факторов среды (см. раздел 6) были выделены основные факторы, связанные с падением уловов и урожайности промысловых рыб. Списки этих факторов для речного ихтиоценоза и для ихтиоценозов водохранилищ не совпадали. Более того, для разных видов рыб, обитающих в водохранилищах, эти списки также различны. Наиболее значимыми оказались следующие факторы: для уловов судака и берша — ХПК и концентрация цинка; для уловов леща — концентрация нитритного азота, взвешенных веществ, хлоридов, pH; для уловов чехони — концентрация азотсодержащих ионов, меди, цинка, температура, водность, pH и БПК
5; для урожайности леща и осетра в Дону — концентрация нитритного азота, гексахлорана, кислорода, фенолов, сульфатов, цинка, pH. Сделан вывод о возможности использовать в качестве биоиндикаторов такие показатели как промысловый возврат, упитанность, жирность рыб.Ряд работ посвящены неким обобщенным представлениям о биоиндикации, т.е. таким универсальным способам, которые пригодны для использования в любом биоме. Так, Д.Раппорт с соавторами (Rapport et al., 1985) сделали обзор некоторых типов стрессов и их симптомов и предложили несколько индикаторов экосистемного стресса:
1) колебания интенсивности круговорота биогенных элементов; 2) колебания величины первичной продукции, что является прямым следствием эвтрофирования или, наоборот, дефицита минеральных ресурсов; более эффективным индикатором является отношение продукции к биомассе, поскольку продукция может как увеличиваться, так и снижаться в ответ на стресс, тогда как величина P/B почти всегда увеличивается (Margalef, 1975); 3) колебания видового разнообразия — наиболее частой реакцией экосистемы на внешнее воздействие является снижение разнообразия 4) ретрогрессия — термин, обозначающий процесс возврата к начальным этапам природной сукцессии; ретрогрессия может выражаться в смене видвого состава в направлении доминирования видов (как правило, с коротким жизненным циклом), более приспособленных к неблагоприятным условиям среды; в результате происходит упрощение структуры сообществ, сами сообщества становятся менее стабильными и начнается новая сукцессия; 5) колебания размерной структуры — наиболее распространенный откликом биоты на стресс является уменьшение среднего размера особи (по крайней мере, временное) доминирующих видов. Данная классификация используется для индикации антропогенного стресса и для поиска факторов, вызывающих стресс в сообществах гидробионтов на различных участках Великих озер в США.В качестве функционального показателя эффективности биотического компонента экосистемы предлагается также использовать ее эксергию (Xu et al., 1999). Эксергия определяется как количество работы, которую может совершить система, когда она приведена в состояние термодинамического равновесия с окружающей средой.
Окружающая среда в состоянии покоя аналогична той, которая была на Земле за 4 миллиона лет до начала эволюции (Jørgensen, Mejer, 1977, 1979). По отношению к состоянию покоя эксергия измеряет расстояние между настоящим состоянием рассматриваемой экосистемы и термодинамическим равновесием. Вероятно, эксергия увеличивается для зрелых экосистем при удалении от термодинамического равновесия. Таким образом, она выражает организованность экосистемы через взаимосвязи живых компонентов. Эксергия экосистемы не может быть измерена, но может быть вычислена для каждого компонента системы путем умножения его средней биомассы на фактор конверсии. Таким образом, суммарный эксергетический индекс экосистемы, выведенный из классической термодинамики, теории вероятности и информационной теории (Jørgensen, 1992a,b, 1994, 1995a,b; Jørgensen et al., 1995) можно записать как:Ex = 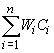 ,
,
где
Ci — биомасса i-го органического компонента экосистемы в г/л или г детрита/л; Wi — факторы конверсии i-го органического компонента. Для различных организмов величина Wi может быть рассчитана исходя из количества генов в клетке (Jørgensen, 1995a,b; Jørgensen et al., 1995).В применении к водным экосистемам Б.Хэннон (Hannon, 1985) предложил применить валовую экосистемную продукцию как экологический индикатор здоровья маршевых приливных экосистем.
Работа по изучению вариабельности динамики биомассы фито-, зоопланктона и зообентоса проведена по данным из 134 загрязненных водоемов на разных континентах (Алимов, 1997). Показано, что вариабельность возрастает пропорционально возрастанию изменчивости температуры воды. Предложен показатель выносливости экосистем, связанный с их продуктивностью, который оказывается низким в водоемах со стабильной температурой. Возрастание этого показателя возможно лишь при увеличении изменчивости температуры и других факторов среды.
В работе Е.Л.Воробейчика с соавторами (1994) приведен обзор работ по регистрации параметров экосистемного уровня в лесных экосистемах. Показателями ухудшения экологического состояния древостоя могут служить уменьшение сомкнутости полога, полноты, плотности и запаса древостоя (Рябинин, 1965; Алексеев, 1982, 1990; McLaughlin, 1985; Степанов, 1988; De Vries, 1988; Черненькова и др., 1989, Likens, 1989; Sienhiegwieg, 1989), снижение его продуктивности (Грешта, 1970; Смит, 1985; McLaughlin, 1985; Шялятене, 1988).
Показатели эффективности применяются и для оценки состояния почвенных экосистем. Из обзора Е.Л.Воробейчика с соавторами (1994) следует, что анализ состояния почвенного микробиоценоза может быть осуществлен двумя путями
— количественным учетом различных групп (видов) или измерением интегральных параметров функционирования. К числу последних относят почвенное дыхание, скорость разложения целлюлозы и других субстратов, интенсивность включения глюкозы и накопления аминокислот, активность азотфиксации, нитрификации (Кобзев, 1980; Левин и др., 1989). При исследовании почвенных угодий Брянской области установлено, что интенсивная агрогенная нагрузка ведет к снижению суммарной биомассы почвенных микроорганизмов, обедняет их видовой состав, вызывает преимущественное развитие олиготрофных фитотоксичных организмов (Гузев и др., 1996). Основными показателями состояния почв могут служить такие показатели, как репродуктивная функция актиномицетов и их качественный состав — наличие представителей группы Niger, величина микробной биомассы, вовлекаемой в круговорот (Мосина, 1996).4.5. Оценка состояния биоты, основанная на отклонениях от нормального функционирования отдельных организмов
Изучая различные морфологические, биохимические, цитогенетические, иммунологические характеристики, заболеваемость растений и животных, населяющих природные биотопы, можно судить об определенных нарушениях в экосистемах, связанных, в том числе, и с влиянием окружающей среды. Понятно, что оценка состояния, вынесенная по данным такого эксперимента, не может быть экстраполирована на весь биоценоз. Тем не менее, в отличие от лабораторных тест-объектов организмы, извлеченные из естественных местообитаний, демонстрируют реакции на весь спектр химических, физических, климатических факторов, характерных для данной экосистемы. Рассмотрим несколько методов, опирающихся на описанный подход.
При цитогенетическом анализе различных организмов была доказана возможность использования содержания микроядер как индикатора степени загрязнения окружающей среды (Кожин и др., 1997). Показана высокая достоверность подобного биохимического скрининга для оценки интегрирующего эффекта антропогенных факторов и для ранжирования отдельных районов по степени экологического неблагополучия.
По результатам 3-летнего изучения лесных сообществ вблизи стартового космического комплекса идентифицированы два типа состояния древостоя — с одной стороны, функционирование в нормальном режиме, когда индикаторные отрицательные отклонения (сокращение средней продолжительности жизни хвои у сосны, дефолиация мелких побегов в верхней части кроны у березы) не выходят за рамки флуктуаций, с другой стороны, когда эти отклонения сохраняются стабильно или усиливаются (Цветков, 1996).
При анализе фенотипической изменчивости одуванчика лекарственного
Taraxacum officinale установлено, что с увеличением уровня загрязнения тяжелыми металлами и нефтепродуктами у особей уменьшалась длина и масса семянок, возрастала доля недоразвитых семянок (Савинов, 1998).Как показало исследование причин летальных мутаций у растения
Arabidopsis thaliana в районе московского района Строгино, увеличение их частоты характерно для мест, расположенных у свалок и рядом с автострадой (Абрамов, Шевченко, 1997). Авторы делают вывод о пригодности данного вида для индикации мутагенности химических соединений.Известны примеры использования гербарных образцов растений для ретроспективного мониторинга загрязнения окружающей среды (Micieta, 1996). Данные анализа тетрад пыльцевых зерен вереска обыкновенного
Calluna vulgaris за 100 лет в различных районах Словакии показали существенное увеличение в последние годы образцов с недоразвитой пыльцой. При этом прослеживается положительная связь этого явления с ростом загрязнений.П.В.Бедова (1997) проводила биоиндикацию речных экосистем бассейна Волги по содержанию в тканях моллюсков каротиноидов. Оказалось, что на умеренно загрязненных участках этот показатель имеет минимальное значение; с увеличением загрязнения растет и содержание каротиноидов. Обнаружена прямая зависимость между данным биотическим индикатором и концентрацией в воде нитратов, нитритов, солей аммония, сульфатов и железа.
Из ракообразных универсальным биоиндикатором загрязненности морской среды может служить амфипода
Ampelisca araucana (Larrain et al., 1998). Пробы донных отложений, взятые в зоне сильного загрязнения залива Сан-Висенте (центральная часть Чили), продемонстрировали значительно большее количество мертвых раков, чем пробы с контрольных участков.Выявлено увеличение плодовитости комнатных мух
Musca domestica по мере удаления от источников техногенного загрязнения (Полякова, 1998). Также мухи из относительно чистых пунктов наблюдения обладали повышенной жизнеспособностью яиц.Исследование ихтиофауны реки, испытывающей влияние фабрики по отбеливанию крафта, показало изменение некоторых морфологических и физиологических показателей у рыб, выловленных ниже сбросов фабрики (
Gibbons et al., 1998а,б). У бычка-подкаменщика Cottus gobio фиксировали отклонения от нормы по упитанности, массе гонад, массе тела и печени (Gibbons et al., 1998а). У лососеокуня Percopsis omiscomaycus отмечали снижение веса и длины тела, а также изменения некоторых биохимических параметров (Gibbons et al., 1998б).В настоящее время все большее количество сторонников появляется у обобщенной оценки благополучия экосистемы путем интегрирования ответа на вопрос о здоровье ее компонентов, представленных разными видами живых существ. Особенностью подобной методологии, названной авторами БИОТЕСТ (Захаров, Кларк, 1993; Захаров, 2000),
является то, что исследуют организмы разных таксономических групп, а интегральным показателем их благополучия предлагают считать эффективность физиологических процессов, обеспечивающих нормальное развитие организма. В нормальных условиях организм реагирует на воздействие среды посредством буферных гомеостатических механизмов. Под воздействием неблагоприятных внешних воздействий эти механизмы могут быть нарушены. Такие нарушения гомеостаза могут наблюдаться до появления изменений, фиксируемых стандартными методами. Поэтому данная методология носит упреждающий, профилактический характер. В методологии БИОТЕСТа обычно используются 5 основных подходов к изучению организмов (Захаров, Кларк, 1993; Захаров, 2000): морфологический, генетический, физиологический, биохимический, иммунологический. Для получения надежной интегральной оценки состояния среды в целом БИОТЕСТ предлагает полнообъемную технологию применения, включающую четыре уровня интегрирования результатов:БИОТЕСТ может быть использован как в отношении живых организмов, так и путем анализа музейных коллекций. Для последней цели пригодны морфогенетические подходы, позволяющие получать информацию о состоянии среды в прошлом.
Одним из методов морфологического подхода БИОТЕСТа является оценка уровня флуктуирующей асимметрии (ФА) билатеральных морфологических признаков растений и животных (Захаров и др., 2000; Гелашвили и др., 2001). Стабильность развития, т.е. способность организма функционировать без отклонений от нормы, есть самый чувствительный показатель состояния природных популяций. В свою очередь оценка ФА представляет собой простейший способ формализации степени этих отклонений. В качестве объектов исследования ФА используются древесные растения, насекомые и мелкие млекопитающие (наземные экосистемы) и рыбы и амфибии (водные экосистемы). При выборе конкретного показателя, характеризующего ФА не существует никаких ограничений — могут быть использованы как качественные, так и количественные показатели, включая меристические (число тех или иных признаков, например пятнышек слева и справа у божьей коровки) и пластические (линейные размеры признаков, например длина прожилок у листьев слева и справа). При анализе комплекса морфологических признаков предлагается использовать интегральный индекс стабильности развития. Для нескольких меристических признаков он рассчитывается как среднее арифметическое количеств асимметричных признаков у каждой особи, деленных на общее количество исследованных признаков. Если измеряются пластические признаки, интегральный индекс равен среднему арифметическому сумм относительных значений асимметрии по всем признакам у каждой особи. Относительное значение асимметрии в данном случае вычисляется как
|L-R|/(L+R), где L и R — размеры признака соответственно с левой и правой стороны.Применительно к позвоночным животным и человеку удобным показателем ухудшения качества экосистем может служить заболеваемость организмов определенными недугами, которые индуцируются факторами окружающей среды. Возникли даже такие понятия как “медицинская экология” (см. например: Келлер, Кувакин, 1998) и “ветеринарная экология” (Уразаев и др., 1997), “экологическая патология” (Слепян, 1998).
Так, Т.И.Моисеенко (1998) на примере оз. Имандра дана методика определения суммарного индекса качества вод и обосновываны информативные экотоксикологические критерии на основе клинической картины заболеваемости рыб. Часто состояние городских экосистем и урбанизированных территорий оценивается по уровням заболеваемости и смертности населяющих их человеческих популяций. Естественно, в расчет должны приниматься заболевания, связанные с употреблением загрязненной воды или пищи, с необходимостью дышать загрязненным воздухом. Хотя более широко следует говорить о связи здоровья социума с целым комплексом природных, техногенных и социогенных факторов (Падкин, 1996).Регистрация респираторных заболеваний и замеры уровней физико-химических факторов в гг. Лондоне, Амстердаме, Роттердаме, Париже и Милане показали достоверную зависимость количества соответствующих обращений к врачу от концентрации озона в атмосфере (
Spix et al., 1998). Установлено также влияние целого ряда факторов окружающей среды на такие показатели как функционирование сердечно-сосудистой системы, нарушение электрической деятельности сердца, возникновение гипертонических кризов и приступов стенокардии (Севостьянова, 1997), уровни репродуктивных потерь (Димитриев и др., 1998). Наиболее же достоверной представляется оценка состояния антропных экосистем, базирующаяся на совокупном анализе нескольких показателей (Селезнев, 1997; Борисов, 1999): средней и относительной продолжительности жизни, среднего возраста, уровня жизни (хотя этот параметр требует выработки соответствующих критериев), а также репродуктивной функции, заболеваемости, медико-географического статуса, физического развития.Примером оценки нормальности некоторых компонентов окружающей среды может служить показатель продолжительности жизни человека. По данным ВОЗ и Минсельхозпрода РФ о влиянии радиоактивного излучения на организм человека установлены количественные соотношения между получаемой дозой и средней продолжительностью жизни (СПЖ) (Ветров, Хрупачев, 1998).
5. Существующие подходы к экологическому нормированию
5.1. Мировая практика разработки экологических стандартов
Согласно обзору Е.Л.Воробейчика с соавторами (1994) начало целенаправленной широкомасштабной деятельности по стандартизации и нормированию неблагоприятных воздействий может быть датировано первой половиной 1970-х гг., когда началось формирование структур управления природопользованием в развитых странах мира. Наряду с охраной вод первоочередными объектами охраны стали леса и их компоненты. Были установлены предельно допустимые концентрации (ПДК) для наиболее загрязняющих веществ в воздухе (Гудериан, 1979; Смит, 1985; The air quality..., 1986; Бялобок, 1988; ECE..., 1988; цит. по Воробейчик и др., 1994). На национальном уровне деятельность по охране природы регламентирована положениями эколого-экономического регулирования Environmental Impact Assessment (EIA), основанной на системе нормативов ПДК, квотах на выбросы для близко расположенных источников загрязнения и на стандартах качества окружающей среды. Такие стандарты существуют в США (The air quality..., 1986; ECE..., 1988) и в других странах. Основной упор в
EIA сделан на возможно полный охват количественными экономическими оценками убытков, наносимых природе ее пользователями. Именно с помощью экономического регулирования достигнуты наиболее значительные успехи в охране окружающей среды. Подобного рода меры оказались гораздо более эффективными, нежели административное принуждение и прямой контроль (Быстрова, 1980; цит. по Воробейчик и др., 1994). В Европе получил развитие расчет критических нагрузок (КН) веществ-загрязнителей (Танканаг, 1997). Под КН понимают максимальное поступление веществ, не вызывающее биогеохимических изменений, которые сопровождают вредные воздействия на экосистемы. Расчет КН принято вести на основе уравнений нединамического масс-баланса. Эти уравнения включают в себя количественную оценку большого числа параметров, характеризующих круговорот загрязнителей в экосистемах. Однако, для многих регионов невозможно определить с достаточной для расчетов точностью входные параметры этих уравнений. Одним из таких регионов является Россия, для которой характерно отсутствие регулярной сети станций по экологическому мониторингу. Вследствие этого необходимо применять методы определения входных параметров через косвенные показатели. Один из таких методов основан на том, что достаточно рассчитать критические нагрузки для небольших, хорошо изученных экосистем, а затем распространить результаты расчетов на всю картируемую территорию. На основании этого метода была создана специализированная экспертно-моделирующая геоинформационная система, с помощью которой был произведен расчет и картографирование величин критических нагрузок азота и серы для Европейской части Российской ФедерацииВ настоящее время во многих странах мира используется экологический стандарт ISO 14001, разработанный Международной организацией по стандартизации (
ISO) и утвержденный в 1996 г. Он предлагает простой, гармоничный подход к управлению охраной окружающей среды, применимый для всех организаций в различных странах мира. Стандарт ISO 14001 содержит в себе все элементы типовой системы управления, такие как стратегия, цели и задачи, программа менеджмента, оперативный контроль, мониторинг и оценка, обучение, внутренние аудиты и анализ менеджмента. Центр внимания данного стандарта сосредоточен на требовании к выполняющим его организациям определить все свои экологически опасные технологические процессы, соответствующие подходы к охране окружающей среды и оценить какие из них являются важнейшими. Текущий анализ менеджмента системы управления окружающей средой и ее отдельных элементов обеспечивает постоянное соответствие, компетентность и эффективность всей экологической программы предприятия (http://www.dnv.ru/). Вообще, система экологического нормирования в западных странах призвана осуществлять три основные функции (Воробейчик и др., 1994). Первая из них — исключение заведомо неприемлемого экологического ущерба. Последний, как правило, пересчитывают в экономический эквивалент. Невыполнение установленных нормативов влечет применение экономических санкций. Вторая функция состоит в регулировании антропогенной нагрузки и затрат на охрану природы таким образом, чтобы сохранялись условия для самовосстановления нарушенных экосистем, но в то же время меры по их защите не препятствовали экономическому росту. Третья функция — стимулирование постоянного снижения антропогенной нагрузки на окружающую среду.О весьма разнообразной практике установления стандартов качества природных вод в странах Европейского Экономического содружества (ЕЭС) подробно пишет в своей книге В.А.Семин (2001). Приведем некоторые примеры из нее, касающиеся особенностей нормирования абиотических факторов среды в отдельных странах.
В национальной системе мониторинга Бельгии каждая отбираемая проба анализируется примерно по 40 параметрам. Две наиболее важные группы показателей относятся к кислородному балансу воды (КБВ) и содержанию в ней тяжелых металлов. Для оценки КБВ рассматривают три ключевых параметра баланса: процент насыщения растворенного кислорода, БПК
5 и содержание аммонийного азота. После того как в пробе определены перечисленные параметры, по каждому параметру по 5-балльной шкале (балл 1 соответствует значениям кислорода — 91-110 %, БПК5 — не более 3 мг/л, аммонийного азота — менее 4 мг/л; балл 5 соответствует значениям кислорода — не более 30 и более 130 %, БПК5 — более 15 мг/л, аммонийного азота — более 5 мг/л) определяют баллы, которые суммируют для получения суммарного значения КБВ. Соответственно качество воды классифицируется от очень хорошего (КБВ = 3-4) до очень плохого (КБВ = 14-15).В Дании в 1983 г. были выделены группы водных объектов и участки с различными характеристиками. Водотоки были разделены на: 1) зоны особого интереса; 2) зоны нереста и нагула мальков лососевых рыб; 3) воды, в которых обитают лососевые; 4) воды, в которых обитают карповые; 5) водотоки со сбором дренажных вод и водотоки, находящиеся под косвенным воздействием сточных вод; 6) водотоки со сборами дренажных и сточных вод; 7) водотоки, находящиеся под воздействием сточных вод и не относящиеся к категории рыбохозяйственных; 8) водотоки, дренирующие пиритные почвы (низкий
pH, осаждение оксидов железа), где фауна сильно поражена. Озера и прибрежные воды делили на 4 типа: 1) зоны особого интереса; 2) воды для купания и для питьевых нужд; 3) воды с естественной разнообразной флорой и фауной; 4) озера, подверженные воздействию стоков, эксплуатации подземных вод и другим влияниям, а также озера, подверженные вредному воздействию сельскохозяйственного производства. Для каждого из видов использования вод были установлены критерии качества, которых следует придерживаться, чтобы достичь, а затем сохранить соответствующее данной цели качество. Например, воды, в которых обитают лососевые рыбы, должны удовлетворять следующим критериям: температура воды — 200С (летом) и 100С (зимой), максимальное изменение температуры при тепловом загрязнении — 10С, растворенный кислород — 6-8 мг/л и 9-12 мг/л (в течение 50% времени), pH — 6-9, максимальное изменение pH при сбросе стоков — 0.5, аммиак — менее 0.025 мг/л, хлор — менее 0.004 мг/л, общий цинк — менее 0.3 мг/л, взвешенные вещества — менее 25 мг/л, БПК5 — не более 3 мг/л, общий аммоний — менее 1 мг/л.Во Франции в 1975 г. была разработана шкала качества поверхностных вод по гидрохимическим показателям на основе анализа проведенной в 1971 г. инвентаризации степени загрязненности водоемов и водотоков по всей стране. Данная шкала состоит из 6 классов качества, где наилучшее качество соответствует 1-му классу, а наихудшее — 4-му, 5-му или 6-му (в зависимости от оцениваемого показателя). Классификации подлежат следующие показатели: температура воды,
0С; pH; осаждение, см3/л; растворенный кислород, мг/л; растворенный кислород, % насыщения; БПК2, мг/л; БПК5, мг/л; окисляемость, мг/л; взвешенные вещества, мг/л; ХПК, мг/л; хлориды, мг/л; сульфаты, мг/л; соли аммония, мг/л; нитраты, мг/л; нитриты, мг/л; натрий, мг/л; калий, мг/л; кальций, мг/л; ртуть, мг/л; гидрокарбонаты, мг/л; фенолы, мг/л; фосфаты, мг/л; СПАВ, мг/л.Химические критерии оценки качества вод в Германии (Баварская служба использования вод) основаны на исследованиях. проведенных ранее в США и Шотландии. Соответствующий метод включает измерение ряда химических параметров в пробах воды с последующим представлением полученной комбинации результатов в виде одного числа — химического индекса, характеризующего обобщенное качество воды. Химически индекс вычисляется как
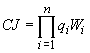 ,
,
где n — число параметров;
qi — подиндекс для i-го параметра (величина между 0 и 100, являющаяся функцией желательности от значения от i-го параметра); Wi — масса i-го параметра (число между 0 и 1), показывающая важность (приоритетность) параметра. Всего при расчете CJ используются значения 8 параметров — растворенный кислород (Wi = 0.2), БПК5 (Wi = 0.2), температура воды (Wi = 0.08), соли аммония (Wi = 0.15), нитраты (Wi = 0.1), фосфаты (Wi = 0.1), pH(Wi = 0.1), электропроводимость (Wi = 0.07). Воды со значением CJ, близким к 100, могут быть отнесены к благополучным, а со значением, близким к 0, — к неблагополучным.В Нидерландах, кроме описанного выше КБВ (применяемого, кроме Бельгии, и в других странах Бенилюкса), применяют показатель содержания общего фосфора. ПДК
Pобщ в Нидерландах равна 0.2 мг/л. Однако с учетом явления эвтрофикации контрольным значением для 6-ти летних месяцев является 0.3 мг/л. В качестве классификационной принята простейшая шкала сравнения полученного значения концентрации с предельным значением. Таким образом, устанавливаются три градации: меньше, того же порядка (0.21-0.3 мг/л) и больше стандарта. Кроме того, в Нидерландах в рамках национальной системы мониторинга ведутся наблюдения за содержанием 6-ти приоритетных металлов: ртути, кадмия, меди, свинца, хрома и цинка. Принцип нормирования здесь тот же, что и в случае с фосфором — устанавливаются три градации качества относительно величин ПДК, которые равны: для ртути — 0.5 мкг/л, для кадмия — 2.5 мкг/л, для меди — 50 мкг/л, для свинца — 50 мкг/л, для цинка — 200 мкг/л, для хрома — 50 мкг/л.В Великобритании классификация рек основана на определении критериев качества, необходимого для конкретных видов водопользования и состоит из четырех основных классов, различающихся значениями содержания растворенного кислорода, БПК
5, концентрации аммонийного азота. Классы качества соответствуют: 1) водам, пригодным для питьевого водоснабжения; 2) рекам, в которых существует промышленное рыболовство ценных видов рыб, и рекреационным зонам; 3) рекам, пригодным для питьевого водоснабжения после предварительной обработки, и рекам с промышленным рыболовством частиковых видов рыб; 4) водам, пригодным для технических нужд.5.2. Российские нормативы предельно допустимых концентраций (ПДК)
В бывшем СССР, а теперь и в России, вся система экологического контроля строится на стандартах предельно допустимых концентраций (ПДК) химических веществ. Результаты лабораторных токсикологических опытов с тест-объектами (Методические указания..., 1998) путем интегрирования полученных сублетальных концентраций (при которых происходит гибель
определенной доли особей) для разных организмов позволяют вычислить используемые в природоохранных документах ПДК. Сегодня ПДК установлены для более чем 1000 химических соединений. Существуют нормативы, регламентирующие состав воды отдельно в водоемах хозяйственно-питьевого и культурно-бытового использования и в водоемах рыбохозяйственного назначения (Мелиорация..., 1988). Исключение составляет оз. Байкал, на бассейн которого распространяются индивидуальные “Нормы допустимого воздействия на экологическую систему Байкала” (Кириенко, Васильева, 1997).В свете современных требований к охране природной среды эта система, основанная на раздельном определении концентраций опасных веществ и сопоставлении их с ПДК, не может быть признана эффективной, поскольку практическое использование концепции ПДК встречается с целым рядом трудностей. Основные из них перечислены в работе В.А.Абакумова и Л.М.Сущени (1991) и приведены в разделе 2.1.
5.3. Модельный анализ влияния абиотических компонентов на природные сообщества.
Для адекватного нормирования потенциально опасных для биоты факторов среды необходима методика, позволяющая сопоставлять некоторые биотические показатели экосистемы со значениями физико-химических характеристик за достаточно продолжительный период времени.
Например, для выявления связи между загрязняющими веществами и биотическими откликами часто используют различные модели, где анализируется зависимость доза — эффект (Криволуцкий и др., 1988; Салиев, 1988; Степанов, 1988, 1990, 1991; Цветков, 1990; Арманд и др., 1991; Комплексная экологическая..., 1992; цит. по: Воробейчик и др., 1994; Hoek et al., 1997; Simpson et al., 1997; Баринова, 1998). Полученные положительные корреляции, однако, дают не вполне точный ответ на вопрос, где на полученных с помощью таких моделей кривых провести границу между благополучием и неблагополучием биоты и получить соответствующую ей предельную норму загрязнителя. Обычно не указывается, каким конкретно образом получены приводимые критические уровни. Вероятнее всего, они определены произвольно — “на глаз” (Воробейчик и др., 1994)
Е.Л.Воробейчик с соавторами (1994) рассматривает три основных подхода к более точному экологическому нормированию. Первый из них представляет собой поиск предельной нагрузки как особой критической точки на кривой доза — эффект, связывающей входные (абиотические нагрузки) и выходные (отклики экосистемы) параметры. Главное условие для определения этой точки — построение в полном объеме дозовой зависимости по экспериментальным данным на всем градиенте нагрузки. В обзоре приведены конкретные функции, использованные для поиска критической точки (
Cate, Nelson, 1971; Beckett, Davis, 1977; Jones, Molitoris, 1984; Singh, Rattan, 1987; Гродзинский, 1988; Пузаченко, 1990).Второй подход выглядит как существенная редукция первого: на основе экспертных оценок определяют единственное значение выходного параметра (вне связи с величинами нагрузок), имеющее смысл границы естественных флуктуаций. Нагрузка, соответствующая выходному параметру в этой единственной точке, принимается за предельную. Согласно данному подходу, предельной нагрузкой является максимально недействующая, при которой индикационные параметры достоверно не отличаются от раз и навсегда установленного контрольного значения. Именно на таких принципах строится гигиеническое нормирование при установлении ПДК. При третьем подходе требуется привлечение “внешней” информации. Например, экономическая целесообразность выращивания сельскохозяйственной культуры определяет допустимый минимальный урожай. Предельная нагрузка, как и во втором подходе, находится через сопоставление с этой величиной.
В системе экологического контроля, разработанной Е.Л.Воробейчиком с соавторами (1994), предлагается при нормировании опираться на методы определения предельной нагрузки как критической точки логистической функции. Причина такого выбора состоит в том, что большинство дозовых зависимостей для экосистемных параметров при техногенном загрязнении имеет вид
S-образной кривой и, следовательно, может хорошо аппроксимироваться логистическим уравнением. При этом места перегибов логистической кривой как раз и представляют собой критические точки или предельные значения, характеризующие переход системы из одного состояния в другое в результате превышения допустимого значения абиотического компонента. Для расчета предельных нагрузок в качестве аппроксимирующего уравнения использовали логистическую кривую вида:![]() ,
,
где
y — оценка параметра, x — оценка нагрузки, a , b — коэффициенты, a0 — минимальный уровень переменной y, A — ее максимальный уровень. С помощью построенных кривых были получены диапазоны предельно допустимых значений содержания тяжелых металлов (Cu, Pb, Cd, Zn) в почве в зависимости от компонента лесной биоты, по которому проводили оценивание (древесный ярус, травяно-кустарничковый ярус, подстилка, почвенный микробиоценоз, почвенная мезофауна, почвенные ферменты, эпифитные лишайники).Данная методика, безусловно, позволяет оценить допустимые значения многих факторов, воздействующих на различные составляющие природных биоценозов в условиях реальной, а не искусственной экосистемы. Тем не менее, остаются непроясненными некоторые вопросы. Например, как воздействует на биоту не каждый из факторов по отдельности, а все они в комплексе, или, другими словами, меняется ли значение предельной нагрузки для одного из факторов при изменении величины любого другого
? Все ли факторы в одинаковой мере важны как причины экологического неблагополучия или их можно ранжировать, исходя из степени потенциальной опасности? Наконец, исчерпывается ли списком факторов, определяемых программой мониторинга в данном природном объекте, угроза нормальному функционированию биоценозов или необходим поиск новых причин экологических рисков?6. Экологически допустимые уровни воздействий на экосистемы
Описанная в разделе 2.2 биотическая концепция контроля природной среды (Левич, 1994) лежит в основе системы экологического нормирования, задача которой — выявить в пространстве абиотических факторов границы между областями нормального и патологического функционирования природных объектов. Такие границы названы экологически допустимыми уровнями (ЭДУ) нарушающих воздействий. Согласно биотическому подходу, оценки экологического состояния на шкале “норма-патология” должны проводиться по комплексу биотических показателей, а не по уровням абиотических факторов. Абиотические же факторы (загрязнения, другие химические характеристики, климатические показатели, интенсивности переносов и др.) должны рассматриваться как агенты воздействия на популяции организмов, на экологические связи между ними и как возможные причины экологического неблагополучия.
Для реализации подобной системы контроля наряду с методами, обеспечивающими индикацию состояния биотического компонента экосистемы, необходимы методы выявления тех физико-химических характеристик экосистемы, которые ответственны за изменение состояния сообщества и его выход за установленные границы нормального существования
(Maximov et al., 1999). Это очевидно должны быть математические методы анализа, позволяющие выделить в многомерном пространстве экологических факторов область экологического благополучия. К этой же группе следует отнести и те математические методы, с помощью которых можно установить ЭДУ для обнаруженных повреждающих воздействий.6.1. Пространство наблюдений, область нормального функционирования и экологически допустимые уровни факторов среды
Совокупность значений биотических и абиотических показателей, синхронизированных по времени и месту отбора проб, может быть наглядно представлена в виде следующего геометрического образа: в многомерном пространстве биотических факторов совокупность наблюдений представлена “облаком” точек (рис. 19А), каждая из которых отмечена маркером оценки состояния (в простейшем случае это два “цвета”, а именно — “хорошо” (нормальное состояние) и “плохо” (патологическое состояние)). В идеальном случае совокупность “хороших” точек образует компактную область нормального функционирования экосистемы. Граница этой области и представляет собой объект исследования для метода ЭДУ. Чтобы без лишних усложнений описать метод, примем дополнительные предположения, упрощающие реальную картину: область нормального функционирования односвязана и адекватно аппроксимируется многомерным кубом. Тогда проекции области нормального функционирования на оси пространства абиотических факторов представляют собой пределы изменения каждого из факторов, выход за которые переводит экосистему из благополучное в неблагополучное состояние. Эти пределы названы экологически допустимыми уровнями (ЭДУ) факторов и отыскиваются “методом ЭДУ” (Левич, Терехин, 1997), о котором пойдет речь в следующем разделе.
Для реальных совокупностей наблюдений границы области нормального функционирования нечетки и размыты (рис. 19Б). Поэтому в методе ЭДУ используются процедуры оптимального распознавания образов, многомерного статистического и детерминационного анализа. Если оценки состояния не бинарны, то метод позволяет получать нормативы различной степени жесткости, сдвиг границы между оценками, объявленными благополучными и неблагополучными, меняет границу области нормального функционирования в пространстве действующих факторов, а с нею — нормативы ЭДУ. Таким образом, появляется возможность вводить дифференцированные нормативы допустимых воздействий для различных категорий природных объектов (например, заповедных зон, рекреаций, хозяйственных территорий, зон дампинга и др.). ЭДУ, полученные на основе оценок по различным биотическим идентификаторам, естественно, могут различаться. Для выбора “истинного” норматива следует, как и в случае отбора оценок состояния, или выбрать приоритетный идентификатор, или, применив принцип наибольшей жесткости, отобрать наиболее безопасный для биоты норматив.
6.2. Использование метода ЭДУ для диагностики и нормирования факторов окружающей среды
Поставленная задача выделения в пространстве факторов области нормального функционирования экосистемы (в форме многомерного параллелепипеда) и расчета границ этой области (т.е. величин ЭДУ) по каждому из факторов решается с помощью метода многомерного анализа данных, который для простоты далее будем называть методом ЭДУ (Замолодчиков, 1992, 1993; Левич, Терехин, 1997; Максимов и др., 2000; Левич и др., 2001). Выход за пределы ЭДУ будем интерпретировать как переход системы из благополучного в неблагополучное состояние.
Реальные границы областей нормального функционирования могут оказаться весьма размытыми. На рис. 20 показано распределение наблюдений для идеального случая одномерного пространства факторов с простой областью нормального функционирования (при всех значениях фактора, меньших ЭДУ, состояние экосистемы благополучно).
Пусть
X — фактор среды (объясняющая переменная), Y — оценка экологического состояния (объясняемая переменная), а ЭДУ, — значение переменной X, превышение которого a priori должно вести к неблагополучной оценке. При этом наблюдение экологически благополучно, если Y < F, и неблагополучно, если Y ³ F, (где F — заданная константа). Кроме того, a (точки в квадранте 1) — число наблюдений, для которых Y < F и X < E; b (точки в квадранте 2) — число наблюдений, для которых Y < F и X ³ E; c (точки в квадранте 3) — число наблюдений, для которых Y ³ F и X < E; d (точки в квадранте 4) — число наблюдений, для которых Y ³ F и X ³ E. В соответствии с этими обозначениями вводятся количественные критерии значимости детерминации "если X ³ E, то Y ³ F": точность T =Определить влияние X на Y — значит, в первую очередь, найти оптимальное значение ЭДУ (или ЭДУ
1 и ЭДУ2 в случае двусторонней границы) при заданном значении F и минимальном пороге точности. Для приведенного на рис. 20 идеального случая точность и полнота для найденного ЭДУ равны 100%Аналогичная диаграмма для реальных данных приведена на рис. 21. Есть несколько причин нарушений идеального случая. Первая из них — статистический разброс и погрешности измерений, в результате чего могут появиться точки в квадрантах 2 и 3 на диаграмме. Вторая причина — воздействие на экосистему факторов среды, отличающихся от рассматриваемого, которые могут вызывать экологическое неблагополучие при значениях исходного фактора, меньших ЭДУ. Это приводит к снижению полноты, т.е. к появлению точек в квадранте 3 на диаграмме, но никак не отражается на точности (не добавляет точек на диаграмме в квадранте 2). Чем более значим данный фактор при объяснении экологического неблагополучия (или чем большее число неблагополучных случаев может быть объяснено превышением ЭДУ именно данного фактора), тем выше критерий полноты.
Вернемся к рис. 21, где приведены результаты анализа влияния на оценку экологического состояния планктона концентрации аммонийного азота — одного из 67 факторов, для которых такой анализ был проведен по данным мониторинга различных водоемов бассейна Дона в 1975-1991 гг. Оценку состояния измеряли по пятибалльной шкале (1 балл — полностью благополучное состояние, 5 баллов — состояние регресса) с точностью 0.5 балла (Абакумов, 1991).
Согласно экологическим модификациям природных сообществ (Абакумов, 1991; Руководство..., 1992). предложено для планктона считать нормальными фоновое состояние и состояние экологического напряжения, неблагополучными — состояния с элементами регресса, а также состояния экологического и метаболического регресса. В терминах кодов оценки граница нормы соответствует величине 2.75. Для зообентоса граница нормы и патологии лежит между состояниями с элементами экологического регресса и состояниями с явно выраженными признаками регресса (код оценки границы 3.75). Нижняя граница точности была задана на уровне 75%. Максимальная полнота P = 42/(42+73)100% = 37% в данном случае достигалась при значении концентрацииКак указывалось ранее, поиск нормативов ЭДУ реализован в процедуре оптимизации (см. раздел 3.2.1.), как составной части детерминационного анализа данных (программное обеспечение "ДА-система" фирмы "Контекст"). При этом программа позволяет построить график зависимости полноты от точности соответствующей детерминации (рис. 22), с помощью которого легко определить, на какой максимум полноты можно рассчитывать при заданном минимальном пороге точности. Итогом оптимизации является нахождение величины ЭДУ, соответствующей некоторому оптимальному сочетанию точности и полноты. Конечно, при таком подходе неизбежно возникает некоторый элемент субъективизма, связанный с выбором этого самого оптимального сочетания.
Чтобы хотя бы немного снизить степень этого субъективизма, можно, например, принять за ЭДУ такое значение объясняющей переменной, при котором величина среднего геометрического точности и полноты максимальна.Если факторов среды несколько, то их однофакторные ЭДУ могут быть рассмотрены в совокупности. Будем относить наблюдение к неблагополучным, если значение хотя бы одного из факторов
X1, X2, ..., Xm превышает свой ЭДУ. Тогда соответствующим образом переопределяются значения a, b, c, d (числа наблюдений). Принимается, что a — число точек, где Y < F и Xi < E для всех Xi; b — число точек, где Y < F и Xi ³ E хотя бы для одного Xi; c — число точек, где Y ³ F и Xi < E для всех Xi; d — число точек, где Y ³ F и Xi. ³ E хотя бы для одного Xi. При таком переопределении a, b, c и d формулы для T и П сохраняют прежний вид. Полученное "суммарное" значение П не меньше одномерных значений, однако объединенная точность может стать меньше минимально допустимого значения.Подобный многофакторный подход, т.е. совместное определение значений ЭДУ всех факторов из условия максимизации совместной полноты при ограничении минимальной допустимой суммарной точностью, более эффективен, так как позволяет выявить синергизм или антагонизм факторов и получить более точные значения ЭДУ.
При многофакторном подходе предлагается следующий алгоритм расчета ЭДУ. Сначала с помощью двухфакторного метода находятся два фактора, дающие наибольшую полноту. После этого к найденному ядру из двух переменных поочередно добавляется каждый из оставшихся факторов. Для каждого из добавляемых факторов вычисляется оптимальное значение ЭДУ и соответствующая ему совместная трехфакторная полнота (значения ЭДУ для переменных ядра берутся из предыдущего анализа и не меняются). В качестве третьего фактора к ядру добавляется тот, которому соответствует максимальная совместная полнота, приводящая к наибольшему ее увеличению при переходе от двухфакторного анализа к трехфакторному. Затем аналогично трехфакторное ядро расширяется до четырехфакторного и т.д.
Описанная процедура была использована для анализа связи между оценкой состояния планктона и 67 факторами среды
в бассейне Дона. Для 12 факторов (БПК5, NH4, NO3, нефтепродукты, фенолы, СПАВ, Cu, Zn, Cr, пестициды, температура), давших наибольшую полноту при одномерном анализе, в табл. 10 приведены соответствующие им однофакторные ЭДУ, точности и значения полноты.В табл. 11 приведены результаты двухфакторного анализа зависимости экологического состояния от загрязняющих переменных. Добавление второго фактора увеличивает полноту с 37 до 48 % (нефтепродукты предпочтительнее использовать, чем содержание цинка, поскольку для них имеются более полные данные). В результате последовательного добавления по одной переменной к исходному ядру из двух переменных, полученному двухфакторным анализом, были оценены следующие значения полноты: для NO
2 — 53% (три фактора), для БПК5 — 56% (четыре фактора), для СПАВ — 57% (пять факторов), для расходов воды — 59% (шесть факторов), для фенолов — 59% (семь факторов).Объединение семи однофакторных ЭДУ дало бы П = 62%, однако при точности всего лишь 70%, тогда как приведенные результаты с П = 59% обеспечиваются с заданной точностью 75%.
Описанные выше многофакторный и гибридный методы чувствительны к наличию множества пропущенных наблюдений, поскольку требуют одновременного присутствия значений многих факторов в каждом наблюдении. Удовлетворить это требование можно с помощью так называемого шагового метода. Он похож на описанный выше метод последовательного ввода факторов, но отличается от него тем, что основан полностью на однофакторных ЭДУ. На каждом шаге ищется новый фактор, дающий наибольший прирост суммарной полноты всех введенных переменных, но его ЭДУ не пересчитывается. На последнем шаге, после включения всех переменных, получают суммарную точность и полноту, о которых упоминалось выше.
Целесообразнее вводить факторы даже не на основании прироста фактической полноты. Ее следует пересчитывать на всю совокупность наблюдений с помощью формулы:
П
общ =где
N2 — число всех неблагополучных наблюдений, для которых Y ³ F. Это позволяет избежать ввода на первых шагах факторов, дающих большой прирост полноты, но при ограниченном числе наблюдений.Шаговый анализ и его результаты позволяют упорядочить факторы по степени их влияния на оценки, а также понять их внутреннюю взаимосвязь. Если группа факторов на первом шаге характеризуется высокой полнотой, а после ввода одного из них на этом шаге все остальные дают малый прирост полноты на втором шаге, то можно утверждать, что их влияние на
Y коррелировано (фактически такой анализ аналогичен анализу частных корреляций в случае количественной переменной Y). Это важно с точки зрения управления качеством среды, поскольку реально влиять на оценку состояния могут и не все эти факторы.После проведения описанных выше процедур метода ЭДУ все участвующие в анализе причин экологического неблагополучия абиотические факторы обычно разделяются на две группы: предзначимые, т.е. те, для которых ЭДУ найдены в пределах наименьшего и наибольшего значений данной переменной в исходно массиве данных, и незначимые, т.е. те, для которых все встречавшиеся в массиве данных значения соответствовали только благополучным оценкам объясняемой биотической характеристики. Отсутствие вычисленной величины ЭДУ для незначимых переменных говорит о том, что соответствующие нормативы для них лежат вне пределов встречавшихся за исследованный период значений. Для предзначимых факторов результатом исследования является вычисленная величина ЭДУ. Однако не все предзначимые факторы могут быть признаны истинными причинами возникающего неблагополучия биоты. Для идентификации таких причин предназначен процесс отбора среди предзначимых факторов значимых, т.е. тех, которые дают наибольший вклад в описание экологического неблагополучия.
Критерии значимости:
— соблюдение минимального порогового значения (как правило, не менее 50%) точности детерминации "превышение ЭДУ влечет неблагополучную оценку"
— высокая полнота соответствующей детерминации;
— достаточное (не менее 30%) количество как благополучных, так и неблагополучных наблюдений;
— некоторые экспертные априорные соображения о влиянии данной переменной среды на данную биотическую характеристику.
Значимые факторы и соответствующие значения их ЭДУ могут быть проранжированы по критерию полноты. В соответствии с этим некоторый фактор, несоблюдение ЭДУ для которого в 80% случаев сопряжено с экологическим неблагополучием, должен быть определен как более значимый, чем фактор, у которого полнота равна 70% (при том же минимальном пороге точности).
6.3. Примеры расчета экологически допустимых уровней и методические возможности метода ЭДУ
В качестве примера приведем результаты работы по экологическому нормированию факторов среды в водных объектах бассейна Дона на основе гидробиологических и физико-химических данных в 1975-1991 гг. (Булгаков и др., 1995, 1997; Левич и др., 1996, 1998). Всего был исследован 31 створ наблюдения (на реках Дон, Маныч, Северский Донец, водохранилищах Цимлянском, Веселовском), на которых отбирали как гидробиологические, так и физико-химические пробы. Оценки состояния соответствующих экосистем проводили по 6 биотическим индикаторам 1) классы качества вод по планктону и перифитону, 2) класс качества вод по зообентосу, 3) уловы судака и берша; 4) уловы леща, 5) уловы чехони; 6) урожайность осетра и леща. Классы качества из пп. 1 и 2 были взяты из классификатора вод Роскомгидромета (Организация и проведение..., 1992).
Граница между нормальными и патологическими состояниями экосистем представляет собой предмет соглашения между исследователями или лицами, принимающими решения. Метод экологических модификаций (Абакумов, 1991; Руководство..., 1992) допускает подвижность этой границы. В разделе 6.2 были приведены и обоснованы соответствующие границы для планктона и зообентоса.
Для ихтиологических переменных определение границы было более сложным. Сначала для каждого из четырех ихтиологических идентификаторов подсчитывали среднемноголетнее значение. Величины уловов и урожайности, входящие в интервал от минимальной величины до средней между минимальной и среднемноголетней величинами, оценивались баллом 3; уловы и урожайность из интервала от средней между максимальной и среднемноголетней величинами до максимальной величины — баллом 1. Промежуточным значениям уловов и урожайности была присвоена оценка 2. Затем для каждого года наблюдений выводилась общая оценка состояния ихтиофауны как среднеарифметическое от оценок для каждого вида рыбы. В некоторых случаях общее состояние ихтиофауны невозможно было оценить каким-либо одним баллом и в результате возникали промежуточные оценки 1-2 и 2-3. К неблагополучному отнесено состояние ихтиофауны с оценками 2-3 и 3, к условно благополучному — с оценками 1, 1-2 и 2. Т.е., под неблагополучием в данном случае понимается снижение годового улова ниже контрольной среднемноголетней отметки. Таким образом, использовалось представление об относительной норме состояния за эталонный период с 1976 по 1990 годы.
Следует подчеркнуть, что поиск абиотических факторов, значимых для возникновение неблагополучия биоты, и вычисление их ЭДУ вели независимо для каждого из указанных выше идентификаторов. Необходимость такого раздельного анализа связана с неустранимой зависимостью результатов поиска ЭДУ от выбранного биотического индикатора. Вовсе необязательно ухудшение класса качества вод по планктону сопровождается, например, снижением уловов или урожайности рыб. Поэтому значения ЭДУ для одного и того же абиотического показателя могут существенно различаться в зависимости от того, какой участок биоценоза мы хотим привести в соответствие с нормой. В этом случае полезным шагом является выработка системы
биологических приоритетов, т.е. выделение наиболее важных с той или иной практической точки зрения компонентов биоты, ЭДУ для которых и являются определяющими. Если подобные приоритеты заранее не предусмотрены, оправданным выглядит выбор из всех полученных ЭДУ наиболее жесткого (например, минимального для загрязняющих веществ и максимального — для концентрации кислорода или прозрачности).Вернемся, однако, к представлению данных для анализа. В качестве абиотических воздействий на биоту рассматривали 34 показателя: концентрации азота аммонийного, азота нитритного, азота нитратного, нефтепродуктов, фенолов, синтетических поверхностно-активных веществ (СПАВ), меди, цинка, взвешенных веществ, кальция, магния, хлоридов, фосфора минерального, железа, марганца, сульфатов, a -гексахлорциклогексана (a -ГХЦГ), g -гексахлорциклогексана (g -ГХЦГ), дихлордифенилтрихлорэтана (ДДТ), дихлордифенилхлорэтана (ДДЭ), БПК
5, ХПК, содержание растворенного кислорода, pH, минерализация, расход воды, температура воды.Метод ЭДУ позволяет использовать при расчетах экологических нормативов не только текущие значения переменных, но и различные типы усреднений. Так, в данном случае для всех гидрохимических характеристик, кроме
pH, анализировали влияние на биоту как экстремальных значений (минимальных для растворенного кислорода и максимальных для всех остальных ингредиентов), так и среднегодовых. Для pH в анализе участвовали среднемесячные значения. Кроме того, в анализ были включены среднемесячные значения расходов и температуры воды. Помимо своего прямого смысла, некоторые из среднемесячных значений непосредственно связаны и с дополнительными экологически значимыми смыслами. Например, мощность весеннего стока, "дружность" весны, длительность маловодного периода, начало распаления льда и т.д.Для расходов воды, температуры и взвешенных веществ в анализе участвовали относительные величины: отношения абсолютных значений к среднемноголетнему для данного створа значению (для расходов воды этот показатель называется водностью). Выбор указанных характеристик объясняется их явной "створоспецифичностью" и адаптированностью локальных створовых сообществ к долговременным условиям обитания. Остальные переменные участвовали в анализе в виде своих абсолютных значений.
Для концентраций биогенных элементов (нитраты, фосфор, аммоний, сульфаты, магний, железо, кальций, марганец), водности, температуры и водородного показателя допустимые границы описывались как в области высоких, так и в области низких значений. Таким образом, область нормального функционирования для этих факторов имела вид, аналогичный изображенному на рис. 5. Для остальных переменных, кроме кислорода, допустимыми считались любые малые значения и граница недопустимости устанавливалась только для высоких значений. Для растворенного кислорода недопустимыми полагались только низкие его значения.
Текущее состояние гидробионтов, безусловно, может зависеть не только от текущего состояния среды, но и от предшествующих им состояний. Чтобы учесть запаздывание реакций гидробионтов на текущие воздействия и эффект накапливания последних, анализировали влияние на организмы значений абиотических переменных в предшествующие годы. Для планктона, перифитона и бентоса анализировали данные за три года (текущий и два предшествующих). Для уловов судака с бершом, леща и чехони — за шесть лет (текущий и пять предшествующих), поскольку основную массу уловов составляли особи от сеголеток до шестилеток. Для урожайности осетра и леща учитывали влияние факторов первой половины текущего года (или для ряда переменных их характеристики за год).
Для каждого из наборов оценок экологического состояния и для каждой соответствующей набору абиотической переменной отыскивали ЭДУ и рассчитывали точность и полноту — критерии значимости этих уровней. Напомним, что все абиотические переменные распадаются на предзначимые и незначимые (раздел 6.2). Результатом исследования для предзначимых факторов является вычисленная величина ЭДУ. Для незначимых факторов результат исследования — минимальная и максимальная границы значений фактора за исследованный период. Эти величины, названные экологически безопасными границами (ЭБГ), при экологическом нормировании могут служить ориентирами границ экологически безопасных значений, которые для данного фактора заведомо не приводят к экологическому неблагополучию. Насколько указанные ЭБГ далеки от потенциально существующих вне их интервала величин ЭДУ остается неизвестным.
В табл. 12 сведены все рассчитанные для бассейна Нижнего Дона ЭДУ и ЭБГ. Для каждой переменной при отборе пороговых величин из конкурирующих значений, получаемых для различных сдвигов по времени, выбирали самое жесткое для данного биотического индикатора. В последнем столбце таблицы сведены самые жесткие ЭДУ среди всех биотических индикаторов. Наибольшая жесткость подразумевает: для всех верхних ЭДУ и ЭБГ — это наименьшее из них значение, для нижних уровней или границ — наибольшее значение.
В соответствии с перечисленными в разделе 6.2 критериями для каждого биотического индикатора были отобраны физико-химические факторы, значимые для возникновения экологического неблагополучия (табл. 13). Нижний порог точности расчета ЭДУ был установлен на уровне 80%. Среднесезонные и среднемесячные значения ЭДУ могут служить ориентировочными нормативами допустимого воздействия того или другого фактора, в соответствии с которыми можно строить природоохранную деятельность в продолжение определенного промежутка времени, т.е. так варьировать уровни сбросов или гидрологические показатели, чтобы к концу месяца или года не выйти за границы предписанной средней величины. В то же время максимальные за год ЭДУ являются прямым руководством к действию, представляя собой по сути нормативы аварийных сбросов химикатов или чрезвычайной гидрологической обстановки. Эти ЭДУ предполагают соблюдение их в любой момент календарного года. Среднесезонные и максимальные за год ЭДУ могут различаться в несколько раз. Так, для зообентоса ЭДУ максимальной концентрации g
-ГХЦГ (0.039) примерно в 3.5 раза превысил ЭДУ среднесезонной концентрации (0.011).ЭДУ для Нижнего Дона были как жестче, так и мягче, чем соответствующие ПДК. Например, более жестки ЭДУ для нитритного и нитратного азота, a-ГХЦГ. Для БПК5, кислорода и цинка ЭДУ и ПДК близки. Для сульфатов, меди, g-ГХЦГ нормативы ЭДУ мягче.
Отметим еще ряд особенностей отдельных идентификаторов и переменных. Суммарная полнота влияния различных факторов для планктона ниже, чем для других биотических показателей — 66% против 85-100%. Это может означать, что среди участвовавших в анализе абиотических переменных не содержатся все те, которые приводят к экологическому неблагополучию планктона, и программа наблюдений за факторами среды экосистем Нижнего Дона должна быть дополнена.
Для фитопланктона донских вод нет недостатка в биогенных элементах, поскольку поиск ЭДУ для них в области низких значений не выявил экологической значимости.
В программах гидрохимического мониторинга анализируется содержание веществ только в водной толще. По-видимому, из-за этой причины концентрации этих веществ не оказались сопряженными с особо неблагополучными (4-5 и 5) оценками состояния зообентоса. Для анализа причин особого неблагополучия этой группы гидробионтов необходимы измерения концентраций загрязняющих веществ непосредственно в грунтах, где вещества накапливаются в иных пропорциях, нежели содержатся в водной толще.
Некоторые из анализировавшихся переменных не должны рассматриваться как причины экологического неблагополучия, поскольку сами могут быть следствиями неудовлетворительного состояния биоты. К таким переменным в определенной степени относятся биохимическое и химическое потребление кислорода, водородный показатель и концентрация растворенного в воде кислорода.
Выше читатель мог заметить, что среди абиотических факторов, использованных для анализа причин экологического неблагополучия, присутствуют не только концентрации химических веществ, как это предусмотрено в концепции ПДК, но и целый ряд иных физико-химических, климатических и гидрологических факторов.
В этом заключается одно из главных достоинств метода ЭДУ — он позволяет включать в процедуру нормирования такие характеристики водной среды обитания как БПК5, ХПК, окисляемость, pH, минерализация, температура воды, водность, уровень радиации и др.Дополнительным результатом нормирования для
pH, относительной температуры, водности являются хронограммы (графики изменения по месяцам года) ЭДУ или ЭБГ их среднемесячных значений. Для водности такие хронограммы называются гидрографами. Пример хронограммы для относительной температуры, влияющей на состояние планктона и перифитона, приведен на рис. 24. Помесячное нормирование указанных физико-химических показателей необходимо при решении следующих проблем экологически безопасного природопользования:Для анализа экологической ситуации необходимы критерии значимости не только индивидуальных переменных, но и заданных их наборов. В разделе 6.2. была подробно описана процедура шагового анализа, позволяющего анализировать все воздействующие факторы в их совокупности. Напомним, что суммарной точностью для набора переменных называется доля неблагополучных наблюдений среди всех наблюдений, где ЭДУ превышено хотя бы в одной переменной из этого набора. Соответственно, суммарная полнота — это доля наблюдений, где ЭДУ превышено хотя бы для одной переменной, среди всех неблагополучных наблюдений.
Суммарная полнота возрастает, если превышающие ЭДУ значения переменной на новом шаге сопутствуют значениям прежней переменной ниже ЭДУ. Если превышения ЭДУ переменной на новом шаге совпадают с превышениями ЭДУ прежними переменными, то суммарная полнота никак не изменится. Назовем существенностью переменной х увеличение суммарной полноты существующего набора переменных при добавлении к нему переменной х
.При выборе для водоохранных мероприятий первоочередного набора значимых переменных важна не только индивидуальная полнота каждой из переменных, но и суммарная полнота отобранного набора в сравнении с другими возможными наборами. Поэтому для значимых переменных важен также анализ их взаимной существенности. Из списка значимых переменных для каждого биотического индикатора составляли различные наборы и для вновь добавляемых переменных вычислялась их существенность. В качестве примера приведена существенность факторов, значимых для возникновения неблагополучия планктона и перифитона (табл. 14). Указанные сведения могут быть полезными тем, кто занимается планированием водоохранных мероприятий. В строке "Шаг 1" таблиц приведены переменные с высокой индивидуальной полнотой. В строке "Шаг 2" указаны переменные, которые наиболее существенны при добавлении к первой переменной из строки "Шаг 1". Переменные из строки "Шаг 3" наиболее существенны при добавлении к набору из первых переменных предыдущих двух строк и т.д. При выборе первоочередных мероприятий существенность выступает важным критерием наряду с другими, например, доступностью переменной для регулирования, экономической и социальной эффективностью регулирования, степенью значимости и т.д.
Учет сразу многих воздействующих на биоту факторов возможен при помощи процедур детерминационного анализа данных (раздел 3.2), когда на основе заданных значений нескольких физико-химических факторов конструируется одна сложная вторичная переменная. В качестве основы для подобного исследования возьмем данные об ЭДУ факторов, приводящих к ухудшению состояния экосистемы р. Суры, которое оценивали по снижению суммарной численности зоопланктона (Максимов и др., 2000). Для концентрации взвешенных веществ, которая обладала наибольшей индивидуальной полнотой среди всех значимых переменных (94%), была создана качественная переменная “значение переменной выходит за границы однофакторного ЭДУ”. Та же процедура была проделана также для трех других произвольно выбранных переменных: pH, концентрации NH
4 и NO2. После этого вычисляли сначала точность и полноту объяснения низкой численности зоопланктона каждой из полученных вторичных переменных в отдельности, а затем путем поочередного добавления к концентрации взвешенных веществ трех других факторов и образования трех новых вторичных переменных исследовали сопряженности типа “если значение хотя бы одной (двух, трех, четырех) переменных выходит за границы ЭДУ, то наблюдается низкая численность зоопланктона” (табл. 15). Как показывают значения полноты, чем большее количество факторов входит во вторичную переменную, тем полнее возникающее экологическое неблагополучие описывается данным набором факторов, поэтому указанный способ анализа решает задачу поиска совокупности факторов, наиболее полно объясняющей выбранное значение индикаторной переменной. Величина полноты 92% для переменной, объединяющей все четыре фактора, свидетельствует о том, что 8% случаев неблагополучия объясняется иными факторами, т.е. существуют ситуации, когда численность снижается при соблюдении ЭДУ по взвешенным веществам, pH, NH4 и NO2.Во всех случаях низкая суммарная полнота при анализе, учитывающем совокупное действие факторов, свидетельствует о том, что причины экологического неблагополучия лежат вне исследованного набора факторов. Например, низкая численность олигосапробных видов зоопланктона в р. Суре была сопряжена с несоблюдением ЭДУ лишь по немногим из определяемых физико-химических показателей (Левич и др., 2001). Вполне вероятно, что снижение численности данной специфической группы видов, обычно заселяющих наиболее чистые воды
, могло быть связано с некоторыми иными факторами неживой природы, не учтенными при анализе. Таким образом, метод ЭДУ дает возможность установить, достаточен или нет набор абиотических факторов среды для наиболее полного выявления возможных причин экологического неблагополучия.Иногда оказывается, что трудно или невозможно определить ЭДУ для того или иного биотического индикатора, работая с полным массивом данных. В этих случаях эффективность анализа может быть повышена за счет выделения по какому-либо признаку (например, пространственному или временному) из общего массива данных более узкого подмассива. На практике подобный контекстный анализ выглядит следующим образом. Для того чтобы выяснить, насколько будут отличаться результаты оптимизации факторов, влияющих на общую численность зоопланктона в р. Суре в зависимости от времени отбора пробы, массив данных был разделен на два подмассива, объединяющих наблюдения соответственно за 1993-1995 (93 наблюдения) и 1996-1997 (106 наблюдений) гг. (Левич и др., 2001).
Обращает на себя внимание факт повышения толерантности зоопланктоценоза по отношению к большинству факторов в 1996-1997 гг. по сравнению с начальным периодом исследования (табл. 16). Диапазоны безопасных (т.е. не приводящих к снижению численности зоопланктона) значений таких факторов, как БПК5, содержание кислорода, концентрации аммонийного азота, углеводородов, фенолов, фосфатов, взвешенных веществ со временем стали шире, что может свидетельствовать о постепенной адаптации сообщества к условиям данного водоема. Интервалы ЭДУ для нитратного, нитритного азота и марганца несколько сузились, хотя и в небольшой степени, что скорее всего говорит о стабилизировавшемся отклике зоопланктона на эти воздействия. Снижение значений ЭДУ для pH — по-видимому, знак того, что произошло смещение зоны толерантности зоопланктонных организмов в сторону более кислой среды.При анализе данных экологического мониторинга с помощью введения контекста можно накладывать на включаемые в анализ данные практически любые необходимые исследователю условия. Например, при поиске значений факторов среды, в пределах которых суммарная численность зоопланктона остается высокой, можно задать контекст, согласно которому будут отобраны те наблюдения, в которых была также высока численность отдельных видов, например, доминирующих в зоопланктоценозе.
После получения нормативов ЭДУ на основе анализа всего массива данных каждое отдельное наблюдение, относящееся к определенному значимому фактору среды, к определенному створу и к определенному периоду (году, месяцу), может быть проанализировано с точки зрения его "вредности" для биотических компонентов экосистемы. Для анализа удобно выразить уровень фактора в долях ЭДУ. Например, если известен ряд наблюдений некоторого фактора по определенному створу за несколько лет, то можно анализировать устойчивость вредного воздействия данного фактора на рассматриваемом створе. Для этого достаточно выразить в "единицах ЭДУ" среднемноголетнее значение фактора на данном створе.
Соответствующая работа для створов Нижнего Дона была проведена по всем значимым факторам каждого из биотических идентификаторов. Из всех створов отобрали те, для которых среднемноголетние величины значимых абиотических переменных выходят за пределы ЭДУ (выше верхних ЭДУ или ниже нижних ЭДУ). Также соблюдали следующее условие: данная переменная на данном створе наблюдалась не менее пяти лет. В результате из 31 исследованного створа бассейна Дона было выделено 15 неблагополучных створов, для которых наблюдалось несоблюдение ЭДУ хотя бы по одному абиотическому фактору и хотя бы для одного из 6 биотических индикаторов.
Для определения статистической достоверности вычисленных ЭДУ может быть использован вариант метода статистического моделирования, называемый “бутстрэпом” (Левич, Терехин, 1997). Он состоит в том, что, например, при определении ЭДУ, генерируется
k выборок x1,....,xk той же размерности, что и исходная выборка, путем случайного выбора наблюдений из исходной выборки, после чего к каждой из полученных k выборок применяют процедуру поиска ЭДУ или оптимизации при детерминационном анализе. В результате в общей сложности находят k значений ЭДУ, точности (Т) и полноты (П): ЭДУ1,....ЭДУk; T1,....Tk; П1,....Пk..По этим значениям находят средние ЭДУm, Tm, Пm, среднеквадратичные отклонения ЭДУs, Ts, Пs и коэффициенты вариации ЭДУv, Tv, Пv, определяемые по формулам:ЭДУ
v = (ЭДУs/ ЭДУm)100%;Tv = (Ts/ Tm)100%;
П
v = (Пs/ Пm)100%.Такого рода анализ был применен к факторам, значимым для экологического неблагополучия, оцениваемого по показателям планктона в водных объектах Дона (табл. 13). Величины ЭДУ
m, ЭДУs и ЭДУv переменных, значимых для возникновения экологического неблагополучия, приведены в табл. 17.7. Приложение метода ЭДУ к региональному контролю пресных вод
7.1. Расчет ЭДУ факторов, значимых для экологического неблагополучия в реках, озерах и водохранилищах бывшего СССР
С помощью метода ЭДУ был проведен анализ причин экологического неблагополучия (определяемого посредством индекса сапробности, биотического и олигохетного индексов) в 10 бассейнах и 11 подбассейнах крупнейших рек бывшего СССР (Замолодчиков, 1993; Булгаков и др., 1995, 1997; Левич и др., 1996, 1998; Максимов и др., 2002а,б):
Для указанных экосистем были рассчитаны ЭДУ физико-химических факторов, значимых для возникновения экологического неблагополучия организмов водной толщи (фито-, зоопланктон, перифитон) и грунтов (зообентос). Кроме того, для незначимых переменных, измеряемых в данном бассейне или подбассейне, использовали ЭБГ. В некоторых экосистемах ЭДУ или ЭБГ факторов были найдены только для одной из групп организмов. Таким образом, с учетом того, что 12 из 21 исследованной экосистемы, были представлены дважды (отдельно для планктонных и бентосных видов), всего получилось 33 набора ЭДУ (табл. 18, 19 и 20). Для сравнения в последнем столбце каждой из таблиц даны значения нормативов ПДК для концентраций соответствующих веществ.
После получения ЭДУ проводили сравнительный анализ бассейнов и подбассейнов (отдельно для европейской и азиатской частей бывшего СССР) между собой по относительной величине ЭДУ или ЭБГ (ОЭДУ), усредненной по 7 переменным, измеряемым во всех экосистемах (Европа), или по 5 переменным, измеряемым в большинстве экосистем (Азия) (Максимов и др., 2002а,б). Для этого минимальное среди всех бассейнов значение ЭДУ или ЭБГ для данной переменной принимали за единицу, а в остальных бассейнах ОЭДУ рассчитывали как отношение его ЭДУ или ЭБГ к минимальному. Например, в европейских экосистемах для NH
4 наименьшим (0,05 мг/л) было значение ЭДУ в бассейне Дуная. Соответственно ОЭДУ для Дуная равнялось 1, для Западной Двины (0,1/0,05) — 2, для Немана (0,38/0,05) — 7,6 и т.д. После того как в каждом бассейне и подбассейне были получены ОЭДУ, для участвовавших в анализе переменных вычисляли среднее по всем переменным значение ОЭДУ. Для европейских экосистем из двух полученных нормативов (для организмов водной толщи и грунтов) отбирали наименьшее (т.е. наиболее жесткое) из двух значений. Для азиатских экосистем в анализ включали оба норматива. Результаты сравнения показаны на рис. 25 и 26.Среди европейских экосистем наименьшую приспособленность к повышению уровней большинства факторов среды продемонстрировали организмы грунтов в бассейне Западной Двины, где зарегистрировано самое низкое значение ОЭДУ. С другой стороны, гидробионты Днепра и Днестра обнаружили наибольшую приспособленность к повышенным концентрациям веществ (особенно NH
4, P и NO2). В целом наблюдается определенная тенденция: самая слабая приспособленность сообществ гидробионтов к существующим внешним нагрузкам наблюдается в бассейнах, расположенных в более высоких широтах, за исключением Дуная и Нижней Волги (Западная Двина, Неман, Верхняя Волга). При этом, хотя среднее значение ОЭДУ для Верхней Волги оказалось выше, чем для Дуная и Нижней Волги, сразу три верхневолжских ЭДУ (по Cu, БПК5 и NO2) были наименьшими среди всех ЭДУ и ЭБГ. Таким образом, хотя температура и не фигурировала среди значимых для неблагополучия факторов ни в одной из экосистем, косвенным образом она влияла на характер взаимодействия в них между живым и неживым компонентами. Вероятно, степень адаптации сообществ южных бассейнов к многолетнему воздействию высоких температур, способствующих усиленному эвтрофированию за счет накопления в водоеме биогенных элементов, оказывается выше, чем у сообществ, “привыкших” к меньшей трофности, обусловленной более низкими концентрациями веществ.Среди азиатских экосистем наиболее высокие значения ОЭДУ как водной толщи, так и грунтов зарегистрированы в бассейне Амура, включая оба подбассейна. Также высоки оказались значения нормативов в Ангаре, Верхнем Енисее и в Енисее в целом. В остальных регионах ОЭДУ значительно ниже, а самые жесткие ЭДУ предъявляются к водным объектам Забайкалья и Лены. Отсюда следует, что экосистемы водных объектов Дальневосточного региона характеризуются наиболее высокой устойчивостью к неблагоприятным воздействиям. Это означает, что только очень высокие концентрации веществ могут привести к возникновению в биоценозе элементов экологического регресса. Отметим, что бассейн Амура уникален также тем, что бентосные организмы здесь более толерантны по отношению к факторам среды, чем представители планктона и перифитона
Что касается бассейна Енисея, то отдельные его участки качественно отличаются друг от друга по степени отклика на внешние воздействия. Если в Забайкальском регионе уже небольшое содержание в воде загрязнителей приводит к неблагополучию оценок, то в водной толще Ангары экологическая обстановка близка к той, что была описана для Амура. То, что средние ЭДУ для бассейнов Амура и Енисея (водная толща) оказались выше ОЭДУ для любого из составляющих подбассейнов, доказывает, что необходима как можно более высокая степень регионализации при нормировании, т.е. по возможности выделение территорий, ограниченных небольшими площадями в пределах водосборного бассейна крупной реки. Понятно, что эта возможность реализуема только при условии достаточного для применения метода ЭДУ количества наблюдений за биологическими и физико-химическими факторами (как минимум 10-20).
7.2. Исследование экосистемы р. Суры на основе биоиндикации по численности зоопланктона
По результатам гидробиологического и физико-химического мониторинга р. Суры в районе Сурского водохранилища выясняли, влияют ли колебания гидрохимических и гидрологических показателей на численность отдельных видов зоопланктона (Максимов и др., 2000). Для оценки такого влияния посредством процедуры оптимизации детерминационного анализа устанавливали, какой интервал на шкале значений абиотических переменных наиболее точно и полно объясняет высокие численности видов, т.е. по сути вычисляли ЭДУ факторов, значимых для снижения численности зоопланктеров. При этом предполагалось, что БПК
5, концентрации Fe, Mn, углеводородов, фенолов и взвешенных веществ могут приводить к снижению численности только в области высоких значений этих показателей, поэтому при оптимизации задавали верхний уровень искомого интервала. Для содержания кислорода ситуация обратная — только снижение этого показателя может приводить к неблагоприятным последствиям для зоопланктона, поэтому фиксировали нижнюю границу интервала. Что касается концентраций аммония, нитритов, нитратов, фосфатов, температуры и pH, то заранее не накладывали никаких условий на их возможные границы, поскольку как слишком высокие, так и слишком низкие значения этих переменных могут вызывать отклонения от благополучного состояния организмов. Так как нужные классы объясняемых переменных (высокие численности видов) получились малонаполненными (для большинства видов — 25-30% от общего числа проб), а количество наблюдений в пределах оптимизируемого диапазона абиотических факторов, наоборот, было большим (как правило, более 50%) нельзя было рассчитывать на высокую точность исследуемых правил: как правило, она не превышала 30-40%. Поэтому при оптимизации задавали нижнюю границу полноты (51%), после чего максимизировали точность.Предварительное изучение сопряженности численностей видов между собой с помощью детерминационного анализа показало, что существуют три организма
Epistylis sp., Euchlanis dilatata и Eudiaptomus gracilis, которые обнаруживают высокие численности при низких обилиях практически всех остальных видов и личиночных стадий, оставаясь при этом отрицательно сопряженными и друг с другом (т.е. высокие численности одного вида сопутствовали низким численностям двух других и наоборот). Оставшиеся 8 видов и 3 личиночные стадии (табл. 21) образуют достаточно устойчивую группу, внутри которой снижение численности всех организмов взаимно сопряжено. Численности 3-х первых видов, как следует из анализа, не сопряжены ни с остальными видами, ни друг с другом.Результаты расчетов (табл. 21) показывают, что 11-видовая группировка взаимно сопряженных по численности зоопланктеров демонстрирует, как правило, однородность по отношению к значениям ЭДУ. Если же рассмотреть отклики 3-х не попавших в указанную группу видов, то заметно, что по отношению ко многим факторам они более толерантны, т.е. ЭДУ этих факторов имеют более широкие границы. Для
Epistylis sp. это относится к концентрациям Fe, Mn, O2, аммония (верхний уровень), нитритов (нижний уровень), фенолов, фосфатов (верхний уровень); для Euchlanis dilatata — к БПК5, концентрациям Fe, O2, Mn, аммония (верхний уровень), нитритов (верхний уровень), углеводородов, фосфатов (верхний уровень), взвешенных веществ, pH (нижний уровень), температуре (верхний уровень); для Eudiaptomus gracilis — к концентрации нитритов (нижний уровень), нитратов (верхний уровень), pH (нижний уровень), фосфатов (верхний уровень), температуре (нижний уровень). Вместе с тем, по большинству показателей найденные для этих 3-х видов ЭДУ существенно различаются, что, видимо, еще раз говорит об особом положении каждого из них в сообществе зоопланктона.***
Описанные в настоящей работе методы контроля природной среды, основанные на биотической оценке экологического состояния, диагностике и нормировании факторов окружающей среды и опирающиеся на гидробиологические и физико-химические базы данных (см. раздел 1), могут лечь в основу экспертно-аналитической системы (ЭС), позволяющей проводить диагностику и нормирование нарушающих экологическое благополучие воздействий, а также поиск путей восстановления нарушенных экосистем. Алгоритмы планируемой ЭС основаны на биотической концепции контроля природной среды (Левич, 1994), согласно которой оценки экологического состояния на шкале “норма — патология” должны проводиться по комплексу биотических показателей, но не по уровням абиотических факторов. Абиотические факторы (загрязнения, другие химические характеристики, климатические переменные, интенсивности переносов) должны рассматриваться как агенты воздействия на популяции организмов и экологические связи между ними.
В планируемой ЭС методы решения поставленных задач реализуются с помощью компьютерной технологии биотического контроля природной среды (Левич, Максимов, 1997), основанной на методе ЭДУ (Левич, Терехин, 1997). В применении к водным экосистемам соответствующий программный продукт позволит решить следующие прикладные задачи:
1) Вычисление индексов сапробности, олигохетного и биотического индексов, класса качества вод по всем группам гидробионтов.
2) Оценка состояния экологических объектов на числовой шкале (индикация состояния). В случае, если оценка проводится по параметрам ранговых распределений численности или биомассы гидробионтов, в ЭС используется программное обеспечение Statistica
.3) Поиск причин экологического неблагополучия среди физико-химических факторов среды (диагностика состояния).
4) Расчеты региональных нормативов экологически допустимых уровней (ЭДУ) физико-химических факторов (экологическое нормирование).
5) Ранжирование физико-химических факторов по их вкладу в степень экологического неблагополучия с указанием значений критериев значимости и существенности этого вклада. Для выполнения этого и предыдущего пунктов необходимо подключение к ЭС программного обеспечения "Детерминационный анализ" (Левич и др., 2001).
6) Экологическое районирование бассейнов, водных объектов по экологическому состоянию, по набору значимых для экологического неблагополучия факторов, по значениям ЭДУ и т.д.
7) Прогноз и экстраполяция экологического состояния водных объектов по сценариям значимых для экологического неблагополучия факторов. Прогноз оценки состояния экосистемы на шкале “норма-патология” осуществляется путём сравнения значений факторов в сценарии предполагаемого воздействия с ЭДУ этих факторов (рис. 27). Прогнозируется благополучное состояние, если значения всех факторов не выходят ха пределы ЭДУ. Неблагополучное состояние прогнозируется, если значение хотя бы одного фактора выходит за пределы ЭДУ.
8) Генерирование и отбор путей восстановления неблагополучных экосистем. Для решения этой задачи необходимо измерить “близость” каждого из воздействующих факторов к границе области нормального функционирования системы и рассчитать диапазон такого изменения факторов, которое необходимо для возврата системы к экологическому благополучию (рис. 28): для восстановления нормального функционирования экосистемы с вектором факторов
B достаточно уменьшить фактор 2 на величину более, чем D ф2B. Для восстановления нормального функционирования экосистемы с вектором факторов C необходимо уменьшить фактор 1 на величину более, чем D ф1C, и вместе с этим фактор 2 — на величину более, чем D ф2C. Отбор путей производится с учётом экономических, технологических, социальных и других издержек для различных вариантов возвращения.9) Выявление пробелов в существующей системе сбора экологических данных.
Подобная ЭС имеет широкий круг областей применения:
1) Экологическое обоснование и планирование природоохранных мероприятий, выбор их приоритетности, оценка их экономических, технологических, экологических, социальных характеристик.
2) Нормирование сбросов загрязняющих веществ, тепловых, физических, климатических и любых других типов воздействий на биоту. Нормирование уровней водопотребления. Прогноз последствий изменения климата.
3) Проведение экологических экспертиз, обследований, паспортизаций, сертификаций, аудита.
4) Создание реестров экологического состояния используемых природных объектов.
5) Аналитическая поддержка экологического мониторинга.
6) Экологическое картирование гидрографических районов.
7) Совершенствование действующих программ экологического мониторинга.
Пользователями ЭС могут в частности быть специалисты по охране природы, органы санэпиднадзора, ресурсные ведомства, проектные организации, службы экологического и медицинского мониторинга, органы экспертизы, органы законодательной, исполнительной и судебной власти.
Благодарности
Авторы выражают свою самую искреннюю благодарность В.А.Абакумову и С.В.Чеснокову за идеи, на которых основаны основаны все ключевые подходы к региональному контролю природной среды, Д.Г.Замолодчикову и А.Т.Терехину, в соавторстве с которыми рождались методы экологической диагностики и нормирования, В.А.Абакумову, Ю.В.Гелетину, Л.В.Джабруевой, В.Г.Дубининой, Н.В.Карташовой, Е.К.Кондрик, Г.Ф.Миловановой, Н.В.Ревковой, соавторам, чьи данные легли в основу реализации основных авторских принципов.
Литература
Абакумов В.А. Экологические модификации и развитие биоценозов // Экологические модификации и критерии экологического нормирования. Труды международного симпозиума. Л.: Гидрометеоиздат, 1991. С.18-40.
Абакумов В.А., Сиренко Л.А. К методу контроля экологических модификаций биоценозов // Научные основы биомониторинга пресноводных экосистем. Труды советско-французского симпозиума. Л.: Гидрометеоиздат, 1988.
Абакумов В.А., Сущеня Л.М. Гидробиологический мониторинг пресноводных экосистем и пути его совершенствования // Экологические модификации и критерии экологического нормирования. Труды международного симпозиума. Л.: Гидрометеоиздат, 1991. С.41-51.
Абакумов В.А., Булгаков Н.Г.,
Левич А.П., Максимов В.Н., Мамихин С.В., Никитина Е.П., Никулин В.А., Сухов С.В. Аналитическая информационная система "Экология пресных вод России" как инструмент биологических исследований // Вестник МГУ. Серия 16. Биол. 2000. №2. С.38-42.Абрамов В.И., Шевченко В.А. Использование арабидопсиса (
Arabidopsis thaliana (L.) Heynh.) для мониторинга загрязнения городской среды Москвы // Тез докл. 3 съезда по радиац. исслед. “Радиобиол., радиоэкол., радиац. безопас.”. Пущино, 1997. С.137-138.Аверинцев В.Г. Оценка сезонной динамики функционального состояния высокоарктических мелководных экосистем Земли Франца-Иосифа методом
ABC // Проблемы экологии полярных областей. М.: Наука, 1991. Вып.2. С.23-24.Аверинцев В.Г., Жуков В.И. Соотношение кумулятивных процентов биомассы и численности как показатель состояния сообществ // Пробл. четверт. палеоэкол. и палеогр. сев. морей. Апатиты, 1987. С.3-4.
Адлер Ю.П., Маркова Е.В., Грановский Ю.В. Планирование эксперимента при поиске оптимальных условий. М.: Наука, 1976. 280 с.
Алексеев В.А. Особенности описания древостоев в условиях атмосферного загрязнения // Взаимодействие лесных экосистем и атмосферных загрязнителей. Таллин, 1982. С.97-115.
Алексеев В.А. Некоторые вопросы диагностики и классификации поврежденных загрязнением лесных экосистем // Лесные экосистемы и атмосферное загрязнение. Л., 1990. С.38-54.
Алимов А.Ф. Динамика биомассы, продуктивность экосистем континентальных водоемов // Ж. общ. биол. 1997. 58. №3. С.27-42.
Арманд А.Д., Кайдакова В.В., Кушнарева Г.В., Добродеев В.Г. Определение пределов устойчивости геосистем на примере окрестностей Мончегорского металлургического комбината // Изв. АН СССР. Сер. геогр. 1991. №1. С.93-104.
Баканов А.И. Использование комбинированных индексов для мониторинга пресноводных водоемов по зообентосу // Вод. ресурсы. 1999. 26. №1. С.108-111.
Баканов А.И. Использование зообентоса для мониторинга пресноводных водоемов // Биол. внутр. вод. 2000. №1. С.68-82.
Баканов А.И., Сметанин М.М., Шихова Н.М. О некоторых подходах к анализу и количественной оценке структур водных экосистем. Ин-т биол. внутр. вод РАН. Борок, 1998. 28 с. Деп. в ВИНИТИ 04.11.98, №3212-В
98.Балушкина Е.В. Применение интегрального показателя для оценки качества вод по структурным характеристикам донных сообществ // Тр. Зоол. ин-та РАН. 1997. 272. С.266-292.
Балушкина Е.В. Критерии и методы оценки уровня антропогенной нагрузки и качества воды // Тез. докл. междунар. науч. конф. “Малые реки: Современное экологическое состояние, актуальные проблемы”. Тольятти, 2001. С.19-20.
Баринова С.С. К оценке состояния водных экосистем архипелага Новая Земля (Новоземельский заповедник, Россия) // Альгология. 1998. 8. №1. С.57-62.
Бедова П.В. Оценка состояния водной среды в Республике Марий Эл с помощью гидробионтов // Тез. докл. Междунар. конф. “Фин.-угор мир: состояние природы и регион. стратегия защиты окруж. среды”. Сыктывкар, 1997. С.21-22.
Борисов Б.М. К вопросу об оценке состояния здоровья населения в условиях антропогенного загрязнения окружающей среды // Экол. пром. пр-ва. 1999. №1. С.3-6.
Булгаков Н.Г. Индикация состояния природных экосистем и нормирование факторов окружающей среды. Обзор существующих подходов // Усп. соврем. биол. 2002.
Т.122. №2. С.115-135.Булгаков Н.Г., Левич А.П., Никонова Р.С., Саломатина Т.В. О связи между экологическими параметрами и продукционными показателями выростного рыбоводного пруда // Вестник МГУ. Сер. биол. 1992. № 2. С.57-62.
Булгаков Н.Г., Дубинина В.Г., Левич А.П., Терехин А.Т. Метод поиска сопряженностей между гидробиологическими показателями и абиотическими факторами среды на примере уловов и урожайности промысловых рыб // Изв. РАН. Сер. биол. 1995. №2. С.218-22
5.Булгаков Н.Г., Левич А.П., Максимов В.Н. Прогноз состояния экосистем и нормирование факторов среды в водных объектах Нижнего Дона // Изв. РАН. Сер. биол. 1997. №3. С.374-379.
Бурлакова Е.Б., Додина Г.П., Зюзиков Н.А., Корогодин В.И., Корогодина В.Л., Красавин Е.А., Когдин В.Н., Маликов А.Н., Петрученко Н.М., Петин В.Г., Решетникова В.И., Шевченко В.А., Шляхтин Г.В., Ярилин А.А. Действие малой дозы ионизирующего излучения и химических загрязнений на человека и биоту. Программа “Оценка сочетанного действия радионуклидных и химических загрязнений” // Атом. энергия. 1998. 85. №6. С.457-462.
Быстрова А.К. Экология и капиталистический город. М.: Наука, 1980. 173 с.
Бялобок С. Регулирование загрязнения атмосферы // Загрязнение воздуха и жизнь растений. Л., 1988. С.500-531.
Ветров В.В., Хрупачев А.Г. Метод оценки и прогнозирования влияния вредных техногенных факторов на продолжительность жизни человека // Вестн. нов. мед. технол. 1998. 5. №3-4. С.15-17.
Воробейчик Е.Л., Садыков О.Ф., Фарафонтов М.Г. Экологическое нормирование техногенных загрязнений. Екатеринбург: Наука, 1994. 280 с.
Вторжение в природную среду. Оценка воздействия. М.: Прогресс, 1983. 191 с.
Вудивисс Ф. Биотический индекс р. Трент. Макробеспозвоночные и биологическое обследование // Научные основы контроля качества поверхностных вод по гидробиологическим показателям. Тр. Советско-английского сем. Л.: Гидрометеоиздат, 1977. С.132-161.
Выхристюк Л.А., Зинченко Т.Д., Шитиков В.К. Метод интегральной оценки экологического состояния речных систем (на примере равнинных рек Среднего Поволжья) // Тез. докл. междунар. науч. конф. “Малые реки: Современное экологическое состояние, актуальные проблемы”. Тольятти, 2001. С.49-50.
Гелашвили Д.Б., Чупрунов Е.В., Радаев А.А. Оценка степени симметрии тест-организмов в биомониторинге наземных и водных экосистем // Тез. докл. междунар. науч. конф. “Малые реки: Современное экологическое состояние, актуальные проблемы”. Тольятти, 2001. С.53.
Грешта Я. Влияние промышленной загрязненности воздуха на сосновые и еловые древостои // Растительность и промышленные загрязнения. Свердловск, 1970. С.20-25.
Гродзинский М.Д. Эмпирические и формально-статистические методы определения областей допустимых и нормальных состояний // Научные подходы к определению норм нагрузок на ландшафты. М., 1988. С.215-224.
Груздева Л.П., Залетаев В.С., Грибовская И.Ф. Изменение компонентов биогеоценозов долины реки Яузы в результате водохозяйственной и другой деятельности (по фонду фундаментальных исследований) // Антропог. загрязнение природ. среды и пути ее оптимиз. 1996. №1. С.120-132.
Гудериан Р. Загрязнение воздушной среды. М.: Мир, 1979. 200 с.
Гузев В.С., Просянников Е.В., Просянникова С.П. Изменения почвенных микробиоценозов и их функционирования в экосистемах, загрязненных выбросами Чернобыльской АЭС // Тез. Докл. 2 съезда О-ва почвоведов. Кн. 1. М., 1996. С.251-252.
Деревенская О.Ю., Мингазова Н.М. Сообщества зоопланктона озер при их загрязнении и восстановлении // Гидробиол. ж. 1998. 34. №4. С.50-55.
Димитриев Д.А., Шарапова О.В., Воронцова Г.М. Влияние антропогенных экологических факторов на уровень мертворожденности // Изв. Нац. акад. наук и искусств Чуваш. Респ. 1998. №3. С.73-77.
Дмитриева Н.В., Обридко С.В. Экологические модификации сообществ фитопланктона и макрозообентоса речного участка Горьковского водохранилища по многолетним данным гидробиологического мониторинга. Ин-т зем. магнетизма, ионосферы и распростр. радиоволн РАН. Троицк, Моск. обл., 1999. 12 с. Деп. в ВИНИТИ 24.02.99, №550-В99.
Дрейпер Н., Смит Г., Прикладной регрессионный анализ. кн.1. М.: Финансы и статистика. 1986. 366 с.
Дробот В.И. Структурные изменения зоопланктонных сообществ водоемов заповедника “Большая Кокшага” // Тез. докл. Междунар. конф. “Фин.-угор мир: состояние природы и регион. стратегия защиты окруж. среды”. Сыктывкар, 1997. С.63-64.
Ежегодники качества поверхностных вод и эффективности проведенных водоохранных мероприятий. 1984—1991. Ростов-на-Дону. Северо-Кавказское территориальное управление по гидрометеорологии.
Ежегодники состояния экосистем поверхностных вод СССР (по гидробиологическим показателям). 1981—1991. Обнинск.
Ежегодные данные о качестве поверхностных вод суши. 1990. Северо-Кавказское территориальное управление по гидрометеорологии.
Ежеквартальные бюллетени качества поверхностных вод суши. 1975—1983. Ростов-на-Дону. Северо-Кавказское территориальное управление по гидрометеорологии.
Жигальский О.А. Экологическое нормирование антропогенных нагрузок // Тез. докл. 3 междунар. конф. “Освоение Севера и пробл. рекультивации”. Сыктывкар, 1997. С.73-75.
Замолодчиков Д.Г. 1992. Оценка экологически допустимых уровней антропогенного воздействия // Докл. РАН. 324, №1. 237—239.
Замолодчиков Д.Г. 1993. Оценки экологически допустимых уровней антропогенного воздействия на пресноводные экосистемы // Проблемы экологического мониторинга и моделирование экосистем. Т.15. СПб. С.214—233.
Замолодчиков Д.Г., Булгаков Н.Г., Гурский А.Г., Левич А.П., Чесноков С.В. К методике применения детерминационного анализа для обработки экологических данных // Научные доклады высшей школы. Биологические науки. 1992. №7. С.116-133.
Захаров В. М. Здоровье среды: концепция. М.: Центр экологической политики России, 2000. 30 с.
Захаров В.М., Кларк Д.М. (ред.) Биотест: интегральная оценка здоровья экосистем и отдельных видов. М.: Московское отделение международного фонда "Биотест", 1993. 68 с.
Захаров В. М., Баранов А. С., Борисов В. И., Валецкий А. В., Кряжева Н. Г., Чистякова Е. К., Чубинишвили А.Т. Здоровье среды: методика оценки. М.: Центр экологической политики России, 2000. 68 с.
ЗинченкоТ.Д., Выхристюк Л.А., Шитиков В.К. Методологический подход к оценке экологического состояния речных систем по гидрохимическим и гидробиологическим показателям // Изв. Самарского научного центра РАН. 2000. 2. №2. С.233-243.
Иванова М.Б. К вопросу об определении состояния озерных экосистем при антропогенном воздействии // Биол. внутр. вод. 1997. №1. С.5-12.
Израэль Ю.А. Экология и контроль состояния природной среды. М.: Гидрометеоиздат, 1984. 435 с.
Калинин В.А., Крюк В.И., Луганский Н.А., Шавнин С.А. Модель оценки состояния пораженных древостоев // Экология. 1991. №3. С.21-28.
Карташева Н.В., Левич А.П. Влияние загрязнения металлами на равномерность распределения численностей видов зоопланктона // Человек и биосфера. М.: Изд-во МГУ, 1981. С.151-155.
Келлер А.А., Кувакин В.И. Медицинская экология. СПб.: "Петроградский и Ко", 1998. 256 с.
Кириенко Г.С., Васильева К.В. Особенности экологической регламентации водохозяйственной деятельности в Байкальском регионе // Сб. науч. тр. 1 Регион. науч. конф. “Пробл. геогр. Байкал. региона”. Улан-Удэ, 1997. С.150-153.
Кобзев В.А. Взаимодействие загрязняющих почву тяжелых металлов и почвенных микроорганизмов (обзор) // Тр. Ин-та эксперимент. метеорологии. 1980. Вып. 10 (86). С.51-66.
Кожин А.А., Алексеенко В.А., Закруткин В.Е. О возможности использования скринингового цитогенетического анализа для оценки степени загрязнения природной среды тяжелыми металлами // Матер. Междунар. симп. “Тяж. мет. В окруж. среде”. Пущино, 1997. С.219-226.
Комплексная экологическая оценка техногенного воздействия на экосистемы южной тайги. М.: ЦЕПЛ, 1992. 246 с.
Кренева С.В., Гусева С.С. Экологические модификации микрозоопланктона как показатель состояния гидробиоценозов // Тр. межд. симп. “Экологические модификации и критерии экологического нормирования”. Л.: Гидрометеоиздат, 1991. С.123-137.
Криволуцкий Д.А., Степанов А.М., Тихомиров Ф.А., Федоров Е.А. Экологическое нормирование на примере радиоактивного и химического загрязнения экосистем // Методы биоиндикации окружающей среды в районах АЭС. М., 1988. С.4-16.
Левин С.В., Гузев В.С., Асеева И.В., Бабьева И.П. Тяжелые металлы как фактор антропогенного воздействия на почвенную микробиоту // Микроорганизмы и охрана почв. М., 1989. С.5-46.
Левич А.П. Структура экологических сообществ. М.: Изд-во МГУ, 1980. 181 с.
Левич А.П. Биотическая концепция контроля природной среды // Доклады РАН. 1994. 337. №2. 280-282.
Левич А.П. Феноменология, применение и происхождение ранговых распределений в биоценозах и экологии как источник идей для техноценозов и экономики // Математическое описание ценозов и закономерности технетики. Абакан: Центр системных исследований. 1996. С.93-105.
Левич А.П., Максимов В.Н. Методическое и программное обеспечение управления качеством природной среды на основе биотической концепции регионального контроля, альтернативной идеологии ПДК // Тезисы докладов 3-й Международной конференции “Проблемы управления качеством окружающей среды” М.: Прима-Пресс, 1997. С.65-69.
Левич А.П., Терехин А.Т. Метод расчета экологически допустимых уровней воздействия на экосистемы (метод ЭДУ) // Водные ресурсы. 1997. №3. С.328-335.
Левич А.П., Терехин А.Т., Булгаков Н.Г., Абакумов В.А., Елисеев Д.А., Максимов В.Н., Качан Л.К. Экологический контроль водных объектов Нижнего Дона по биотическим идентификаторам планктона, перифитона и зообентоса // Вестник МГУ. Сер. биол. 1996. №3. С. 18-25.
Левич А.П., Булгаков Н.Г., Абакумов В.А., Терехин А.Т. Определение экологически допустимых уровней расходов воды по гидробиологическим показателям // Вестник МГУ. Сер. 16. Биол. 1998. №3. С.49-52.
Левич А.П., Максимов В.Н, Булгаков Н.Г. Методика применения детерминационного анализа данных мониторинга для целей экологического контроля природной среды // Успехи соврем. биол. 2001. Т.121. №2. С.131.
Лихачева Н.Е., Левич А.П., Кольцова Т.И. О количественной обработке проб фитопланктона. Ранговые распределения численностей фитопланктона пролива Вилькицкого // биол. науки. 1979. №9. С.102-106.
Лугаськов А.В., Ярушина М.И., Лугаськова Н.В., Степанов Л.Н. Экологическое состояние водной биоты речных экосистем на территории Курганской области. Ин-т экол. раст. и живот. УрО РАН. Екатеринбург, 1998. 48 с. Деп. в ВИНИТИ 14.01.98, №32-В98.
Максимов B.Н. Об одном способе оценки качества природных вод // Самоочищение и биоиндикация загрязненных вод. М.: Наука, 1980, С. 212.
Максимов В.Н. Проблемы комплексной оценки качества природных вод (экологические аспекты) // Гидробиологический ж. 1991а. 27. №3. С.8-13.
Максимов В.Н. Ранговый метод оценки сходства сообществ при анализе состояния экосистем // Экологические модификации и критерии экологического нормирования. СПб.: Гидрометеоиздат, 1991б. С.329-333.
Максимов В.Н. О ранговых распределениях в экологии сообществ с точки зрения статистики // 2003 (в печати).
Максимов В.Н., Ганьшина Л.А., Абакумов В.А. Оценка качества воды в реке по видовому составу фитопланктона // Известия АН СССР, сер. биол. 1983. N 5. С.731.
Максимов В.Н., Андрющенко В.В., Морозов В.А., Симонов А.И. Оценка состояния морских экосистем по данным химического и биологического мониторинга // Проблемы фонового мониторинга состояния природной среды. 1987. Вып.5. С.140.
Максимов В.Н., Джабруева Л.В., Булгаков Н.Г., Терехин А.Т. Концепция выявления стрессовых состояний водных экосистем методом ранговых распределений и экологически допустимые уровни загрязняющих веществ для водоемов р. Элиста // Водные ресурсы. 1997а. 24. №1. С.79-85.
Максимов В.Н., Булгаков Н.Г., Джабруева Л.В. Ранговые распределения размерно-морфологических групп микроводорослей в перифитоне и их связь с уровнем загрязнения водоема // Известия РАН. Сер. Биол. 1997б. №6. С.697-704.
Максимов В.Н., Булгаков Н.Г., Милованова Г.Ф. Детерминационный анализ связей между различными компонентами экосистем. Сравнение с методами традиционной статистики // Известия РАН. Сер. биол. 1999. № 4. С.469-477.
Максимов В.Н., Булгаков Н.Г., Милованова Г.Ф., Левич А.П. Детерминационный анализ в экосистемах: сопряженности для биотических и абиотических компонентов // Изв. РАН. Сер. биол. 2000. №4. С.482-491.
Максимов В.Н., Абакумов В.А., Булгаков Н.Г., Левич А.П., Терехин А.Т. Экологически допустимые уровни абиотических факторов. Исследование водных экосистем Восточной Европы // Вестник МГУ. Сер. 16. Биол. 2001. №4. С.36-41
Максимов В.Н., Абакумов В.А., Булгаков Н.Г., Левич А.П., Терехин А.Т. Экологически допустимые уровни абиотических факторов. Исследование пресноводных объектов азиатской части России и Узбекистана // Изв РАН. Сер. биол. 2002.
№5. С.614-624.Мелиорация и водное хозяйство. Справочник. 5. Водное хозяйство / Ред. Бородавченко И.И. М.: Агропромиздат, 1988.
Методические указания по установлению эколого-рыбохозяйственных нормативов (ПДК и ОБУВ) загрязняющих веществ для воды водных объектов, имеющих рыбохозяйственное значение. М.: Изд-во ВНИРО, 1998. 145 с.
Михайловский Г.Е. Описание и оценка состояний планктонных сообществ. М.: Наука, 1988. 214 с.
Моисеенко Т.И. Экотоксикологический подход к нормированию антропогенных нагрузок на водоемы Севера // Экология. 1998. №6. С.452-461.
Мосина Л.В. Новые подходы к оценке антропогенных воздействий в экосистемах с использованием биоиндикаторов // Тез. докл. 2 Съезда О-ва почвоведов. М., 1996. Кн.1. С.40-41.
Мэгарран Э. Экологическое разнообразие и его измерение. М.: Мир, 1992. 181 с.
Носов В.Н., Булгаков Н.Г., Максимов В.Н. Построение функции желательности при анализе данных экологического мониторинга // Изв. РАН. Сер. биол. 1997. №1. С.69-74.
Оксиюк О.П., Жукинский В.Н., Брагинский Л.П., Линник Г.Н., Кузьменко М.И., Кленус В.Г. Комплексная экологическая классификация качества поверхностных вод суши // Гидробиол. ж. 1993. Т.29. №4. С.62-76.
Организация и проведение режимных наблюдений за загрязнением поверхностных вод суши на сети Роскомгидромета. Методические указания. Охрана природы. Гидросфера. РД 52.24.309-92. СПб.: Гидрометеоиздат, 1992. 67 с.
Оценка состояния и устойчивости экосистем. М., 1992. 125 с.
Падкин В.В. Популяционное здоровье как критерий экологической безопасности урбанизированного региона // Регион. экол. 1996. №1-2. С.89-92.
Пареле Э.А., Астапенок Е.Б. Тубифициды (
Tubificidae, Oligochaeta) — индикаторы загрязнения водоема // Изв. АН ЛатвССР. 1975. №9. С.44-46.Песенко Ю.А. Концепция видового разнообразия и индексы, его измеряющие // Ж. общ. биол. 1978. Т.39.. №3. С.380-293.
Петин В.Г., Жураковская Г.П., Пантюхина А.Г., Рассохина А.В. Малые дозы и проблемы синергического взаимодействия факторов окружающей среды // Радиац. биол. радиоэкол. 1999. 39. №1. С.113-126.
Полякова Ю.Б. Комнатная муха
Musca domestica L. (Diptera, Muscidae) как биоиндикатор техногенного загрязнения окружающей среды // Энтомол. обозрение. 1998. 77. №2. С.289-294, 523.Попченко В.И. Закономерности изменения сообществ донных беспозвоночных в условиях загрязнения природной среды // Тр. сов.-франц. симп. Л.: Гидрометеоиздат, 1988. С.136-140.
Попченко В.И. Экологические модификации сообществ зообентоса в условиях загрязнения водных экосистем //. Экологические модификации и критерии экологического нормирования. Л.: Гидрометеоиздат, 1991. С.144-151.
Попченко В.И. Экологические модификации сообщества макрозообентоса как индикаторы загрязнения водных экосистем // Биоиндикация: теория, методы, приложения. Тольятти, 1994. С.38-52.
Пузаченко Ю.Г. Проблемы устойчивости и нормирования // Структурно-функциональная организация и устойчивость биологических систем. Днепропетровск, 1990. С.
122-147.Пузаченко Ю.Г., Пузаченко А.Ю. Семантические аспекты биоразнообразия // Ж. общ. биол. 1996. Т.57. №1. С.1-43.
Раддэм Г.Г., Казаков Ю.Е., Вышковская Н.В. Экологические модификации в закисленных водоёмах // Экологические модификации и критерии экологического нормирования. Л.: Гидрометеоиздат, 1991. С.75-80.
Руководство по гидробиологическому мониторингу пресноводных экосистем / Ред. Абакумов В.А. СПб: Гидрометеоиздат, 1992. 318 с.
Рябинин В.М. Лес и промышленные газы. М.: Лесн. пром-ть, 1965. 112 с.
Рябко Б.Я., Кудрин Б.И., Завалишин Н.Н., Кудрин А.И. Модель формирования статистической структуры биоценоза // Изв. АН СССР. Сер. биол. 1978. Вып.1. С.121-127.
Савинов А.Б. Анализ фенотипической изменчивости одуванчика лекарственного (
Taraxacum officinale Wigg.) из биотопов с разными уровнями техногенного загрязнения // Экология. 1998. №5. С.362-365.Салиев А.В. Моделирование воздействия атмосферных фитотоксикантов на растения — пространственный аспект // Основы биологического контроля загрязнения окружающей среды. М., 1988. С.137-160.
Сахаров В.Б. Оценка состояния байкальского фитопланктона методом функции желательности // Биол. науки. 1982. №5. С.64-68.
Сахаров В.Б., Ильяш Л.В. Применение метода функции желательности к анализу результатов изучения действия цинка и хрома на фитопланктон Рыбинского водохранилища // Биол. науки. 1982а. №8. С.65-68.
Сахаров В.Б., Ильяш Л.В. Метод функции желательности при анализе сезонной сукцессии планктона // Биол. науки. 1982б. №1. С.59-66.
Севостьянова Е.В. Кардиометеопатии — проявление экологического неблагополучия // Матер. Науч.-практ. Конф. “Сиб. стандарт жизни: экол., образ., здоровье”. Новосибирск, 1997. С.165-167.
Селезнев И.С. О комплексных показателях безопасности малых городов // Безопасность. 1997. №5-6. С.47-51.
Сиренко Л.А. Экспресс-методы изучения экологических модификаций фитоценозов // Экологические модификации и критерии экологического нормирования. Л.: Гидрометеоиздат, 1991. С.151-163.
Сироткина Н.В., Левич А.П. Влияние тяжелых металлов на видовую и надвидовую структуры фитопланктонного сообщества Рыбинского водохранилища // Человек и биосфера. М.: Изд-во МГУ, 1981. С.142-150.
Слепян Э.И. Принципы экологической патологии // Регион. экол. 1998. №1. С.53-79.
Смит У.Х. Лес и атмосфера. Взаимодействие между лесными экосистемами и примесями атмосферного воздуха. М.: Прогресс, 1985. 429 с.
Степанов А.М. К методике расчета индекса деградации биогеоценоза под воздействием выбросов промышленных предприятий // Мониторинг лесных экосистем. Каунас, 1986. С.201-202.
Степанов А.М. Методология биоиндикации и фонового мониторинга экосистем суши // Экотоксикология и охрана природы. М., 1988. С.28-108.
Степанов А.М. Экспериментальное определение допустимой антропогенной нагрузки на лесные экосистемы // Проблемы устойчивости биологических систем. Харьков, 1990. С.352-353.
Степанов А.М. Биоиндикация на уровне экосистем // Биоиндикация и биомониторинг. М., 1991. С.59-64.
Тальских В.Н. Использование концепции инвариантных состояний биоценозов в экологическом мониторинге и нормировании загрязнения рек Средней Азии // Экологические модификации и критерии экологического нормирования. Л.: Гидрометеоиздат, 1991. С.163-184.
Тальских В.Н. Биологическая шкала оценки качества воды и экологического состояния водотоков Средней Азии на основе ранжирования “биологического отклика” биоценозов перифитона // Тр. Среднеаз. регион. н.-и. гидрометеорол. ин-та. 1998. №155. С.57-60, 179, 187, 195.
Тамарина Н.А., Максимов В.Н., Александрова К.В., Георгиева Е.К. Функция желательности как обобщенный критерий качества лабораторных культур насекомых // Журнал общей биологии. 1981. N 4. С.597.
Танканаг А.В. Расчет и картографирование величин критических нагрузок по азоту и сере на экосистемы Европейской части России // Тез. докл. 2 Откр. гор. науч. конф. мол. ученых г. Пущино. Пущино, 1997. С.199-200.
Уиттекер Р. Сообщества и экосистемы. М.: Прогресс.1980. 102 с.
Уразаев Н.А., Никитин А.В., Нелупенко Л.В. Ветеринарная экология и патология животных // Вестн. ветеринарии. 1997. 4. №6.С.13-16.
Фащук Д.Я. Географо-экологическая модель морского водоема. Автореф. дис. ... докт. геогр. наук. М., 1997.
Федоров В.Д. Особенности организации биологических систем и гипотеза "вспышки" вида в сообществе // Вестник МГУ. Сер. 16. Биология. 1970. №2.
Федоров В.Д. Новый показатель неоднородности структуры сообщества // Вестн. МГУ. Сер. биол. 1973. №2. С.94-96.
Федоров В.Д. Относительное обилие симпатрических видов и модель экспоненциально разломанного стержня // Человек и биосфера. М.: Изд-во МГУ, 1978. Вып.2. С.17-41.
Федоров В.Д., Кондрик Е.К., Левич А.П. Ранговое распределение численности фитопланктона Белого моря // Докл. АН. 1977. Т.236. №1. С.264-267.
Федоров В.Д., Сахаров В.Б., Левич А.П. Количественные подходы к проблеме оценки нормы и патологии экосистем // Человек и биосфера. М.: Изд-во МГУ, 1982. Вып.6. С.3-42.
Хан Г., Шапиро С. Статистические модели в инженерных задачах. М.: Мир. 1969. 395 с.
Цветков В.Ф. Параметры критических этапов техногенной деградации сосновых насаждений Кольского полуострова // Тез. докл. конф. “Проблемы устойчивости биологических систем”. Харьков, 1990. С.330-331.
Цветков В.Ф. Нормирование влияния компонентов ракетного топлива на лесную растительность // Тез. докл. междунар. науч. конф. “Влияние атмосф. загрязнения и др. антропог. и природ. факторов на дестабилиз. состояния лесов Центр. и Вост. Европы”. Т.1. М., 1996. С.49-51.
Черненькова Т.В., Степанов А.М., Гордеева М.М. Изменение организации лесных фитоценозов в условиях техногенеза // Ж. общ. биол. 1989. 50. №3. С.388-394.
Чесноков С.В. Детерминационный анализ социально-экономических данных. М.: Наука, 1982. 168 с.
Шитиков В.К., Зинченко Т.Д., Головатюк Л.В. Математические аспекты оценки патологии экосистем на примере зообентоса малых рек Самарской области // Тез. Докл. Междунар. науч. конф. “Малые реки: Современное экологическое состояние, актуальные проблемы”. Тольятти, 2001. С.230.
Шялятене Я.А. Закономерности усыхания сосняков в зоне интенсивных промышленных выбросов // Лесн. хоз-во. 1988. №2. С.43-46.
Экологический мониторинг. Методы биологического и физико-химического мониторинга. Часть
III: Учебное пособие / Под ред. проф. Д.Б.Гелашвили. Н. Новгород: Изд-во ННГУ, 1998.Экологический мониторинг. Методы биологического и физико-химического мониторинга. Часть
IV: Учебное пособие / Под ред. проф. Д.Б.Гелашвили. Н. Новгород: Изд-во ННГУ, 2000. 427 с.Beckett P.H., Davis R.D. Upper Critical levels of toxic elements in plants // New phytol. 1977. 79. Pp.95-106.
Berger W.H., Parker F.L. Diversity of planctonic Evraminifera in deepsea sediments // Science. 1970. V.168. №3937. Pp.1345-1347.
Beukema J.J. An evaluation of the ABC-method as applied to macrozoobenthic communities living on tidal flats in the Dutch Wadden Sea // Mar. Biol. 1988. V.99. Pp.425-433.
Calow P. Ecological risk assessment: Risk for what? How do we decide? // Ecotoxicol. and Environ. Safety. 1998. 40. №1-2. Pp.15-18.
Cate R.B. Jr., Nelson L.A. A simple statistical procedure for partitioning soil test correlation data into two classes // Soil Sci. Soc. Amer. Proc. 1971. 35. Pp. 658-660.
De Vries W. Critical deposition levels for nitrogen and sulfurs on dutch forest ecosystems // Water, Air and Soil Pollut. 1988. 42. №1-2. Pp.221-239.
ECE Critical Levels Workshop. United Nations Economic Commission for Europe. Final Draft Report. Bad Harzburg, 1988. 146 pp.
Engle V.D., Summers J.K., Gaston G.R. A benthic index of environmental condition of Gulf of Mexico estuaries // Estuaries. 1994. 17. №2. Pp.372-384.
Fager E.M. Diversity: a sampling study // Am. Natur. 1972. V.106. Pp.293-310.
Frontier S. Diversity and structure in auatic ecosystems // Oceanogr. and Mar. Biol. Annual Rev. 1985. V.23. Pp.253-278.
Gallup S.D., Robertson J.M., Streebin E. A comparison of macroscopic and microscopic indicators of pollution // Proc. Okla. Acad. Sci. 1970. V.50. Pp.49-56.
Gibbons W.N., Munkittrick K.R., Taylor W.D. Monitoring aquatic environments receiving industrial effluents using small fish species 1: Response of spoonhead sculpin (Cottus ricei) downstream of a bleached-kraft pulp mill1. Environ. Toxicol. and Chem. 1998а. 17. №11. Pp.2227-2237.
Gibbons W.N., Munkittrick K.R., McMaster M.E., Taylor W.D. Monitoring aquatic environments receiving industrial effluents using small fish species 2: Comparison between responses of trout-perch (Percopsis omiscomaycus) and white sucker (Catostomus commersoni) downstream of a pulp mill. Environ. Toxicol. and Chem. 1998б. 17. №11. Pp.2238-2245.
Gibson L.B. Contribs Cushman Foundat. Foraminiforal // Res. 1966. V.17. №4. Pp.117-124.
Gleason H.A. On the relation between species and area // Ecology. 1922. V.3. №1. Pp.156-162.
Good I.J. The population frequencies of species and the estimation of population parameters // Biometrika. 1953. V.40. Pp.237-264.
Goodnight C.J., Whitley L.S. Oligochaetes as indicators of pollution // Proc. 15th Indust. Waste Conf. Purdue Univ. Eng. Ext. 1961. Ser.106. №45. Pp.139-142.
Gorham-Test C. The 1993 Regional Environmental Monitoring and Assessment Program (R-EMAP) study of Galveston Bay, Texas. Pap. Spring Meet. Gulf Estuar. Res. Soc. (GERS) // Gulf Res. Repts. 1998. 10. March. P.75.
Halffter G. A strategy for measuring landscape biodiversity // Biol. Int. 1998. №36. Pp.3-17.
Hannon B. Ecosystem flow analysis // Can. Bull. Fish. Aquat. Sci. 1985. 213. Pp.97-118.
Heip C.A. A new index measuring evenness // J. Mar. Biol. Assoc. U.K. 1974. V.54. №3. Pp.555-557.
Hill M.O. Diversity and evenness: a unifying notation and its consequences // Ecology. 1973. V.54. №2. Pp.427-432.
Hoek G., Groot B., Schwartz J.D., Eilers P. Effects of ambient particulate matter and ozone on daily mortality in Rotterdam, the Netherlands // Arch. Environ. Health. 1997. 52. №6. Pp.455-463.
Jones R.H., Molitoris B.A. A statistical method for determining the breakpoint of two lines // Anal. Biochem. 1984. 141. №1. Pp.287-290.
Jørgensen S.E. Integration of Ecosystem Theories: a Pattern. Kluwer, Dordrecht, 1992a.
Jørgensen S.E. Parameters, ecological constraints and exergy // Ecol. Model. 1992б. 62. Pp.163-170.
Jørgensen S.E. Review and comparison of goal functions in system ecology // Vie Milieu. 1994. 44. №1. Pp.11-20.
Jørgensen S.E. Exergy and ecological buffer capacities as measures of ecosystem health // Ecosyst. Health. 1995a. 1. №3. Pp.150-160.
Jørgensen S.E. The application of ecological indicators to assess the ecological condition of a lake // Lakes Reservoirs: Res. Manage. 1995b. 1. Pp.177-182.
Jørgensen E.S., Mejer H. Ecological buffer capacity // Ecol. Model. 1977. 3. Pp.39-61.
Jørgensen S.E., Mejer H.F. A holistic approach to ecological modelling // Ecol. Model. 1979. 7. Pp.169-189.
Jørgensen S.E., Nielson S.N., Mejer H.F. Energy, environ, exergy and ecological modelling // Ecol. Model. 1995. 77. Pp.99-109.
Kaitala S., Maximov V.N. The desirability function in evaluation of the response of phytoplankton communities to toxicants // Toxicity Assessment. An international quarterly. 1986. V.1. N 1. P.86.
Karr J.R., Dudley D.R. Ecological perspective on water quality goals // Environ. Manag. 1981. 5. Pp.55-68.
Kay J.J., Schneider E.D. Thermodynamics and measurements of ecosystem integrity // Ecological Indicators / Ed. McKenzie D. Elsevier: Amsterdam, 1991. Pp.159-182.
Larrain A., Soto E., Bay-Schmith E. Assessment of sediment toxicity in San Vicente bay, Central Chile, using the amphipod Ampelisca araucana // Bull. Environ. Contam. and Toxicol. 1998. 61. №3. Pp.363-369.
Levich A. P. Variational modelling theorems and algocoenoses functioning principles // Ecological modelling. 2000. 131. Pp.207-227.
Likens G.E. Some aspects of air pollutant effects on terrestrial ecosystems and prospects for the future // AMBIO. 1989. 18. №3. Pp.172-178.
MacArthur R.H. Fluctuations of animal populations and measure of community stability // Ecology. 1955. V.36. №7. Pp.533-536.
MacArthur R.H. On the relative abundance of species // Amer. Nat. 1960. V.94. Pp.25-36.
Margalef R. Diversidad de especies en las comunidades naturales // Publnes. Inst. Biol. Apl. Barcelona. 1951. V.9. №5.
Margalef R. La teoria de la informacion en ecologia // Mem. Real. Acad. Cienc. Artes Barcelona. 1957. V.32. P.373-449.
Margalef R. Temporal succession and spatial heterogeneity in phytoplankton // Perspectives in Marine Biology. Berkeley: University of California Press, 1958. Pp.327-347.
Margalef R. Human impact on transportation and diversity in ecosystems. How far is extrapolation valid? // Proc. 1st Int. Congr. of Ecology. Structure, functioning and management of ecosystems. The Hage, Sept. 8-14, 1974. Centre for Agricultural Publishing and Documentation: Wageningen, Netherlands, 1975. Pp.237-241.
Maximov V.N., Bulgakov N.G., Levich A.P. // Environmental indices: Systems Analysis Approach. London: EOLSS Publishers, 1999. P.363.
McIntosh R.P. An index of diversity and the relation of certain concepts of diversity // Ecology. 1967. V.48. Pp.392-404.
McLaughlin S.B. Effect of air pollution on forest // Air Pollution Control Association. 1985. 35. Pp.512-534.
McRae G., Camp D.K., Lyons W.G., Dix T.L. Relating benthic infaunal community structure to environmental variables in estuaries using nonmetric multidimensional scaling and similarity analysis // Pap. 3rd Symp. Environ Monit. Ans Assess. Program. (EMAP). Environ Monit. And Assess. 1998. 51. №1-2. Pp.233-246.
Meire P.M., Dereu J. Use of the abundance/biomass comparison method for detecting environmental stress: some considerations based on intertidal macrozoobenthos and bird communities // J. Appl. Ecol. 1990. V.27. №1. Pp.210-221.
Menchinick E.F. A comparison of some species-individuals diversity indices applied to samples of field insects // Ecology. 1964. V.45. Pp.859-861.
Mičieta K., Murín G. Využitie herbárových položiek na spätný biomonitoring znečistenia živothého prostredia // Zivot. prostred.
1996. 30. №5. 262-263.P.J.Morin. Community ecology. London: Blackwell Science Inc, 1999. 424 pp.
Motomura I. Statistical treatment of association // Japan J. Zool. 1932. V.44. Pp.379-383.
Odum H.T., Cantlon J.E., Kornicker L.S. An organizational hierarchy postulate for the interpretation of species-individuals distributions, species entropy and ecosystem evolution and the meaning of a species variety index // Ecology. 1960. V.41. Pp.395-399.
Pantle R., Buck H. Die biologische Überwachung der Gewässer und Darstellung der Ergebnisse // Gas- und Wasserwach. 1955. 96. №8. S.1-604.
Peet R.K. The measurement of species diversity // Ann. Rev. Ecol. System. 1974. V.5. Pp.285-307.
Pereira L.A.A., Loomis D., Conceição G.M.S., Braga A.L.F., Arcas R.M., Kishi H.S., Singer J.M., Böhm G.M., Saldiva P.H.N. Association between air pollution and intrauterine mortality in São Paulo, Brazil // Environ. Health Perspect. 1998. 106. №6. Pp.325-329.
Pielou E.C. The measurement of diversity in different types of biological collections // J. Theor. Biol. 1966. V.13. Pp.131-144.
Pielou E.C. Ecological diversity. New York — London — Sydney — Toronto: Wiley Interscience Publ., 1975.
Preston F.M. The commonness and rarity of species // Ecology. 1948. 29. №3. Pp.254-283.
Rapport D.J., Regier H.A., Hutchinson T.C. Ecosystem behavior under stress // Am. Nat. 1985. 125. Pp.617-640.
Shannon, C.E., Weaver W. The Mathematical Theory of Communication. Urbana, Illinois: Univ. of Illinois Press, 1949.
Sheldon A.L. Equitability indices: dependence on the species count // Ecology. 1969. V.50. №3. Pp.466-467.
Sienhiegwieg J. Forest community changes as bioindicators of contaminations // Proc. 14th Int. Meet. “Air Pollut. And Forest Decline”. Birmensdorf, 1989. 1. Pp.245-248.
Simpson E.H. Measurement of diversity // Nature. 1949. V.169. P.688.
Simpson R.W., Williams G., Petroeschevsky A., Morgan G., Rutherford S. Associations between outdoor air pollution and daily mortality in Brisbane, Australia // Arch. Environ. Health. 1997. 52. №6. Pp.442-454.
Singh A.K., Rattan R.K. A new approach for estimating the phytotoxicity limits // Environ. Monit. and Assess. 1987. 9. №3. Pp.269-283.
Sivadasan K.K., Joseph K.J. Community structure of microalgal benthos in the Cochin backwaters // Indian J. Mar. Sci. 1998. 27. 3-4. Pp.323-327.
Slădecek
V. System of water quality from the biological point of view // Arch. Hydrobiol. Ergeb. Limnol. 1973. №7. 218 pp.Spang W.D. Bioindikation in Rahmen raumrelevanter Planungen — Grundlagen, Bedeutung, Indikatorwahl // Heidelberg. geogr. Arb. 1996. №100. S.75-87.
Spix C., Anderson H.R., Schwartz J., Vigotti M.A., Le Tertre A., Vonk J.M., Touloumi G., Balducci F., Piekarski T., Bacharova L., Tobias A., Ponka A., Katsouyanni K. Impact a court terme de la pollution atmosphérique sur les admissions hospitalières pour maladies respiratoires en Europe: Synthèse quantitative des études APHEA // Energ.-sante. 1998. 9. №3. Pp. 368-371.
Stevenson R.J. Diatom indicators of stream and wetland stressors in a risk management framework // Pap. 3rd Symp. Environ. Monit. and Assess. Program (EMAP). Environ. Monit. and Assess. 1998. 51. №1-2. Pp.107-118.
The air quality standard for SO2 and particles (Directive SO2/779/EEC) and its significance for the other main air pollutants: Commission of the European Communities. Final Report. Luxembourg, 1986. 221pp.
Warwick R.M. A new method for detecting pollution effects on marine macrobenthic communities // Mar. Biol. 1987. V.95. №2. Pp.193-200.
Watanabe T. et al. Saprophilous and eurysaprobic diatom taxa to organic water pollution and diatom assemblage index (DAIpo) // Diatom. 2. 1986. Pp.23-73.
Watanabe T., Asai K., Houki A. Numerical water quality monitoring of organic pollution using diatom assemblages // 9th Diatom Symposium. 1988а. Pp.123-141.
Watanabe T., Asai K., Houki A. Biological information closely related to the numerical index DAIpo (Diatom Assemblage Index to Organic Water Pollution) // Diatom. 1988б. 4. Pp.49-58.
Weber L.M., Isely J.J. Water quality assessment of the Chattooga River using a macroinvertebrate biotic index // J. E. Mitchell Sci. Soc. 1997. 113. №2. Pp.37-45.
Whittaker R.H. Dominance and diversity in land plant communities // Science. 1965. V.147. Pp.250-260.
Woodiwiss F.S. The biological system of stream classification used by the Trent River Board // Chem. and Ind. 1964. 11. Pp.433-447.
Xu F.-L., Jørgensen S.E., Tao S. Ecological indicators for assessing freshwater ecosystem health // Ecol. Model. 1999. 116. Pp.77-106.
Таблица 1.
Поля гидробиологической базы данных|
Категория переменных |
Названия полей |
|
1) Место и дата |
Гидрографический район Бассейн Подбассейн Водный объект Створ Год Месяц Число Время суток |
|
2) Экологические группировки гидробионтов |
Экологическая группировка организмов |
|
3) Условия отбора проб |
Вертикаль, доля ширины реки от левого берега Глубина, м Температура воды, градусы Цельсия (для фитопланктона и зоопланктона) Характер субстрата (для перифитона) Тип грунта (для зообентоса) Тип растительности (для зообентоса) Прозрачность воды (для фитопланктона) |
|
4) Таксономическая принадлежность для фитопланктона |
Отдел Род Вид |
|
5) Таксономическая принадлежность для зоопланктона |
Систематическая группа организмов (отряд, семейство) Род Вид |
|
6) Таксономическая принадлежность для перифитона |
Род Вид |
|
7) таксономическая принадлежность для зообентоса |
Систематическая группа организмов (тип, класс) Род Вид |
|
8) Количественные показатели для сообщества фитопланктона |
Число видов Численность, 103 кл/мл Биомасса, мг/л |
|
9) Количественные показатели для отделов фитопланктона |
Число видов Численность, 103 кл/мл Биомасса, мг/л |
|
10) Количественные показатели для видов фитопланктона |
Численность, % Частота встречаемости, баллы Линейные размеры, мкм Объем, мкм3 |
|
11) Количественные показатели для сообщества зоопланктона |
Число видов Численность, тыс. экз/м3 Биомасса, мг/м3 |
|
12) Количественные показатели отрядов/семейств зоопланктона |
Число видов Численность, тыс. экз/м3 Биомасса, мг/м3 |
|
13) Количественные показатели видов зоопланктона |
Возрастная стадия Относительная численность, % Индивидуальный вес, мг/тыс. экз |
|
14) Количественные показатели для сообщества бактериопланктона донных отложений |
Численность сапрофитов, млн. клеток/мл Нефтеокисляющие бактерии (титр) |
|
15) Количественные показатели для сообщества бактериопланктона поверхностных вод |
Общее количество бактерий, млн. кл./мл Численность сапрофитных бактерий, млн. кл./мл Отношение общего количества бактерий к количеству сапрофитных бактерий Время удвоения сапрофитных бактерий, час Время удвоения бактерий в целом, час Количество спороносных бактерий, млн. кл./мл Нефтеокисляющие бактерии (титр) |
|
16) Количественные показатели сообщества перифитона |
Число видов Частота встречаемости, баллы Индивидуальная сапробность |
|
17) Количественные показатели полного сообщества зообентоса на грунте |
Число видов Численность, экз./м2 Биомасса, г/м2 |
|
18) Количественные показатели полного сообщества зообентоса на растительности |
Число видов |
|
19) Количественные показатели типов/классов зообентоса на грунте |
Число видов Численность, экз./м2 Биомасса, г/м2 |
|
20) Количественные показатели типов/классов зообентоса на растительности |
Число видов |
|
21) Количественные показатели видов зообентоса на грунте |
Относительная численность, % |
|
22) Показатели для макрофитов |
Тип грунта Проективное покрытие, % Число видов Характеристика распространения растительности Фенофаза |
|
23) показатели для пигментных характеристик фитопланктона |
Концентрация хлорофилла "a", мкг/л Концентрация хлорофилла "c", мкг/л Отношение концентраций хлорофилла "a" и "c" Пигментный индекс |
Таблица 2.
Поля физико-химической базы данных|
Категория переменных |
Названия полей |
|
1) Гидрологические характеристики |
Скорость течения, расход воды, уровень воды, прозрачность |
|
2) Гидрохимические показатели |
Содержание растворенного кислорода, БПК5, ХПК, pH, окисляемость, жесткость воды, сумма ионов, минерализация |
|
3) Концентрации загрязняющих веществ |
Азот аммонийный, азот нитратный, азот нитритный, азот органический, алюминий, ванадий, взвешенные вещества, висмут, гексахлоран, a -гексахлорциклогексан, g -гексахлорциклогексан, ДДД, ДДТ, ДДЭ, железо, кадмий, калий, кальций, карбофос, кобальт, кремний, ксантогенаты, лигнин, лигносульфонат, линдан, магний, марганец, медь, метанол, метафос, метилмеркаптан, молибден, мочевина, мышьяк, натрий, нефтепродукты, никель, НСО, олово, пестициды, роданиды, ртуть, свинец, серебро, сероводород, синтетические поверхностно-активные вещества, смолистые вещества, сульфаты, титан, углеводороды, фенолы, формальдегид, фосфамид, фосфор минеральный, фосфор общий, фосфор органический, фтор, фториды, хлориды, хлорофос, хром, цианиды, цинк |
Таблица 3
. Характеристики переменных, использованных при анализе данных|
Переменные |
Единицы измерения |
Число проб |
Минимум |
Максимум |
Асимметрия |
Эксцесс |
||||||
|
Щелочность |
мг-экв/л |
121 |
2.85 |
512 |
3.60 |
18.78 |
||||||
|
БПК |
мг О/л |
214 |
0.32 |
432 |
14.53 |
212.08 |
||||||
|
Кальций |
мг/л |
158 |
10.02 |
62 |
0.21 |
-0.74 |
||||||
|
Кадмий |
мг/л |
206 |
0 |
2 |
14.35 |
205.87 |
||||||
|
Хлориды |
мг/л |
214 |
0.83 |
60 |
5.06 |
32.95 |
||||||
|
Кобальт |
мг/л |
214 |
0 |
0.04 |
4.48 |
36.77 |
||||||
|
ХПК |
мг О/л |
73 |
3.9 |
120.96 |
2.78 |
10.21 |
||||||
|
Хром |
мг/л |
214 |
0 |
0.052 |
5.47 |
35.76 |
||||||
|
Медь |
мг/л |
210 |
0 |
0.02 |
3.22 |
13.04 |
||||||
|
Железо |
мг/л |
214 |
0.01 |
5.88 |
3.75 |
21.36 |
||||||
|
Жесткость |
мг-экв/л |
119 |
0.8 |
8.7 |
1.60 |
4.84 |
||||||
|
Калий |
мг/л |
127 |
0.85 |
34.8 |
8.10 |
80.36 |
||||||
|
Кислород |
мг/л |
174 |
4.6 |
18.48 |
0.95 |
2.90 |
||||||
|
Магний |
мг/л |
113 |
0.608 |
79.04 |
3.12 |
14.89 |
||||||
|
Марганец |
мг/л |
214 |
0 |
0.98 |
6.16 |
57.97 |
||||||
|
Натрий |
мг/л |
127 |
2 |
25 |
1.24 |
4.27 |
||||||
|
Азот аммонийный |
мг/л |
214 |
0.04 |
34.5 |
12.81 |
178.69 |
||||||
|
Никель |
мг/л |
214 |
0 |
0.2 |
7.67 |
68.99 |
||||||
|
Нитриты |
мг/л |
214 |
0 |
1.58 |
6.40 |
52.97 |
||||||
|
Нитраты |
мг/л |
214 |
0.02 |
6.5 |
2.78 |
9.32 |
||||||
|
Нефтепродукты |
мг/л |
186 |
0 |
6.9 |
12.72 |
168.66 |
||||||
|
Свинец |
мг/л |
214 |
0 |
4.5 |
12.36 |
163.61 |
||||||
|
рН |
214 |
5.5 |
9.56 |
-0.33 |
0.24 |
|||||||
|
Фенолы |
мг/л |
213 |
0 |
0.412 |
14.46 |
210.41 |
||||||
|
Сухой остаток |
мг/л |
214 |
112 |
1092 |
4.95 |
42.59 |
||||||
|
Фосфаты |
мг/л |
214 |
0 |
10.5 |
11.72 |
155.60 |
||||||
|
Сульфаты |
мг/л |
214 |
2.4 |
100 |
2.59 |
14.30 |
||||||
|
Температура |
0 С |
178 |
0 |
30 |
-1.17 |
0.38 |
||||||
|
Взвешенные вещества |
мг/л |
214 |
0.4 |
1714 |
14.25 |
206.33 |
||||||
|
Цинк |
мг/л |
214 |
0.001 |
0.26 |
5.61 |
37.70 |
||||||
|
Bosmina coregoni |
тыс. экз./л |
101 |
0.001 |
2596.75 |
6.75 |
49.50 |
||||||
|
Bosmina longirostris |
тыс. экз./л |
92 |
0.007 |
68.6 |
4.79 |
24.85 |
||||||
|
Chydorus sphaericus |
тыс. экз./л |
93 |
0.01 |
166 |
6.47 |
43.23 |
||||||
|
Daphnia cucullata |
тыс. экз./л |
67 |
0.02 |
486.6 |
6.50 |
47.76 |
||||||
|
Daphnia longispina |
тыс. экз./л |
83 |
0.007 |
578.67 |
4.75 |
23.77 |
||||||
|
Epistilys sp. |
тыс. экз./л |
44 |
0.02 |
47.5 |
2.92 |
8.75 |
||||||
|
Euchlanis dilatata |
тыс. экз./л |
81 |
0.02 |
8 |
3.58 |
14.42 |
||||||
|
Eudiaptomus sp. |
тыс. экз./л |
48 |
0.01 |
200.8 |
4.68 |
24.05 |
||||||
|
Eudiaptomus gracilis |
тыс. экз./л |
56 |
0.01 |
26 |
4.57 |
23.44 |
||||||
|
Keratella quadrata |
тыс. экз./л |
104 |
0.007 |
57.28 |
7.38 |
62.00 |
||||||
|
Личинки копепод |
тыс. экз./л |
151 |
0.007 |
93.2 |
5.09 |
31.07 |
||||||
|
Личинки других групп |
тыс. экз./л |
86 |
0.007 |
37 |
2.85 |
9.16 |
||||||
|
Mesocyclops leuckartii |
тыс. экз./л |
73 |
0.02 |
64 |
5.24 |
34.00 |
||||||
|
Науплии |
тыс. экз./л |
166 |
0.007 |
81.6 |
4.32 |
19.71 |
||||||
Таблица 4.
Классификация качества воды водоемов и водотоков по гидробиологическим показателям (Организация и проведение..., 1992)|
Класс качества вод |
Степень загрязненности воды |
По фитопланктону, зоопланктону, перифитону |
По зообентосу |
По бактериопланктону |
|||
|
Индекс сапробности по Пантле и Букку (в модификации Сладечека), баллы |
Отношение общей численности олигохет к общей чиленности донных организмов, % |
Биотический индекс по Вудивиссу, баллы |
Общее количество бактерий, 106 кл/мл |
Количество сапрофитных бактерий,103 кл/мл |
Отношение общего количества бактерий к количеству сапро фитных бактерий |
||
|
I |
Очень чистые |
Менее 1.0 |
1-2 |
10 |
Менее 0.5 |
Менее 0.5 |
Более 103 |
|
II |
Чистые |
1.00-1.50 |
21-35 |
7-9 |
0.5-1.0 |
0.5-5.0 |
Более 103 |
|
III |
Умеренно загрязненные |
1.51-2.50 |
36-50 |
5-6 |
1.1-3.0 |
5.1-10.0 |
103-102 |
|
IV |
Загрязненные |
2.51-3.50 |
51-65 |
4 |
3.1-5.0 |
10.1-50.0 |
Менее 102 |
|
V |
Грязные |
3.51-4.0 |
66-85 |
2-3 |
5.1-10.0 |
50.1-100.0 |
Менее 102 |
|
VI |
Очень грязные |
Более 4.00 |
86-100 или макробентос отсутствует |
0-1 |
Более 10 |
Более 100 |
Менее102 |
Примечание: Допускается оценивать класс качества воды и как промежуточный между
ii-iii, iii-iv, iv-vТаблица 5.
Градации биологических показателей для вычисления балльной оценки экологического состояняи водного объекта (Зинченко и др., 2001)|
Показатели макрозообентоса |
Размерность |
Баллы |
|||
|
1 |
2 |
3 |
4 |
||
|
Пределы изменения показателей |
|||||
|
Численность |
экз./м 2 |
0-500 |
501-1000 |
1001-100001 |
>10000 |
|
Биомасса |
г/м 2 |
1-5 |
5.1-10 |
10.1-15 |
>15 |
|
Количество видов |
экз. |
0-5 |
6-10 |
11-15 |
>15 |
|
Индекс Шеннона |
бит/экз. |
0-1 |
1.1-2 |
2.1-3 |
>3 |
|
Биотический индекс Вудивисса |
0-2 |
2-4 |
4-6 |
>6 |
|
|
Индекс Пареле |
0.81-1 |
0.56-0.8 |
0.3-0.55 |
<0.3 |
|
Таблица
6. Видовая структура сообществ птиц в сыром жестколистном лесу Австралии (Driscoll, 1977)|
Вид |
Обилие (количество экземпляров на участке) |
|
Какаду |
103 |
|
Розелла |
115 |
|
Зимородок-хохотун |
13 |
|
Лирохвост |
2 |
|
Полосатый рамфомикрон |
67 |
|
Бурый рамфомикрон |
36 |
|
Белобровый крапивник |
51 |
|
Пламенный меланодриас |
8 |
|
Южный желтый меланодриас |
6 |
|
Серая веерохвостая мухоловка |
61 |
|
Золотой свистун |
10 |
|
Коллурицинкла |
21 |
|
Австралийская трещотка |
7 |
|
Белогорлая пищуха |
65 |
|
Краснобровая пищуха |
4 |
|
Желтолицый медосос |
49 |
|
Белоухий медосос |
92 |
|
Белобрюхий медосос |
37 |
|
Тропидоринх |
16 |
|
Вьюрок |
6 |
|
Курравонг |
23 |
|
Ворон |
9 |
|
Рыжая веерохвостая мухоловка |
2 |
|
Мухоловка |
6 |
|
Рыжий свистун |
5 |
|
Фалькункул |
4 |
|
Парадалот |
1 |
|
Белоглазка |
3 |
|
Лунный медосос |
1 |
|
Аканторинх |
9 |
|
Сорока |
2 |
Таблица 7.
Примеры индексов разнообразия|
Формула |
Авторы |
|
|
Berger, Parker, 1970 |
|
S = |
Simpson, 1949; Whitteker, 1965 |
|
|
McIntosh, 1967 |
|
|
Gibson, 1966 |
|
|
Fager, 1972 |
|
H = |
MacArthur, 1955; Margalef, 1957 |
|
B = |
Pielou, 1975 |
|
C km = |
Good, 1953; Hill, 1973 |
|
|
Pielou, 1966; Peet, 1974 |
|
|
Margalef, 1958 |
|
|
Sheldon, 1969 |
|
|
Heip, 1974 |
|
|
Федоров, 1973 |
|
T a = |
Hill, 1973 |
|
|
Gleason, 1922; Margalef, 1951 |
|
|
Menchinick, 1964 |
|
|
Odum et al., 1960; Gallup et al., 1970 |
|
|
Gallup et al., 1970 |
Таблица 8.
Проверка соответствия распределения видов птиц 1-й модели Мак-Артура при разбиении эмпирической совокупности на октавы|
Верхняя граница класса |
Число видов в классе |
Предсказание модели |
Число видов в объединенных классах |
Предсказание модели |
|
1 |
2 |
1.077 |
||
|
2 |
3 |
1.040 |
||
|
4 |
3 |
1.074 |
8 |
4.092 |
|
8 |
6 |
3.558 |
6 |
3.558 |
|
16 |
5 |
5.775 |
||
|
32 |
2 |
7.614 |
7 |
13.389 |
|
64 |
5 |
6.636 |
5 |
6.636 |
|
128 |
5 |
2.566 |
5 |
2.417 |
Таблица 9.
Проверка соответствия распределения численности птиц 1-й модели Мак-Артура с разбиением на терции|
классы |
исходное разбиение |
объединенные классы |
||
|
верхняя граница |
число видов в классе |
предсказание модели |
число видов в классе |
предсказание модели |
|
1 |
2 |
1.077 |
||
|
3 |
4 |
2.045 |
6 |
3.122 |
|
9 |
10 |
5.342 |
10 |
5.342 |
|
27 |
5 |
10.646 |
5 |
10.646 |
|
81 |
7 |
9.919 |
||
|
243 |
3 |
1.417 |
10 |
11.336 |
Таблица 10
. Одномерные параметры зависимости оценки экологического состояния планктона и перифитона от абиотических факторов (N — число наблюдений; N1 — число благополучных наблюдений; N2 — число неблагополучных наблюдений; min и max — наименьшее и наибольшее за период наблюдений значения фактора).|
Переменная |
N |
N1 |
N2 |
min |
ЭДУ |
max |
Точность, % |
Полнота, % |
|
БПК 5, мг/л |
231 |
116 |
115 |
1.03 |
5.39 |
9 |
77 |
15 |
|
NH4 , мг/л |
231 |
116 |
115 |
0.007 |
0.99 |
7.35 |
75 |
37 |
|
NO2 , мг/л |
231 |
116 |
115 |
0.004 |
0.2 |
0.92 |
76 |
11 |
|
Нефтепродукты, мг/л |
231 |
116 |
115 |
0.015 |
0.63 |
2.02 |
75 |
23 |
|
Фенолы, мг/л |
231 |
116 |
115 |
0 |
0.009 |
0.017 |
75 |
10 |
|
СПАВ, мг/л |
231 |
116 |
115 |
0 |
0.12 |
0.2 |
75 |
13 |
|
Cu, мг/л |
225 |
114 |
111 |
0.001 |
0.017 |
0.07 |
78 |
13 |
|
Расход воды, м 3/с |
231 |
116 |
115 |
8 |
77.48 |
310 |
80 |
7 |
|
Zn, мг/л |
173 |
93 |
80 |
0 |
0.092 |
0.15 |
75 |
4 |
|
Cr, мг/л |
9 |
0 |
9 |
0.005 |
0.005 |
0.016 |
100 |
100 |
|
Пестициды, мкг/л |
110 |
64 |
46 |
0 |
0.086 |
0.15 |
100 |
2 |
|
Температура, 0С |
77 |
46 |
31 |
8 |
12.53 |
18 |
100 |
3 |
Таблица 11.
Двумерный анализ связи оценки состояния планктона и перифитона с различными парами абиотических факторов (обозначения и размерности те же, что и в табл. 10)|
Пары факторов |
N |
N1 |
N2 |
ЭДУ1 |
ЭДУ2 |
Точность,% |
Полнота,% |
|
БПК5 — NH4 |
231 |
116 |
115 |
5.419 |
1.027 |
75 |
44 |
|
БПК5 — NO2 |
231 |
116 |
115 |
4.957 |
0.233 |
75 |
34 |
|
БПК5 — Нефтепродукты |
231 |
116 |
115 |
5.650 |
0.628 |
76 |
32 |
|
БПК5 — Фенолы |
231 |
116 |
115 |
5.419 |
0.009 |
76 |
25 |
|
БПК5 — СПАВ |
231 |
116 |
115 |
6.112 |
0.106 |
79 |
23 |
|
БПК5 — Cu |
225 |
114 |
111 |
6.112 |
0.013 |
79 |
30 |
|
БПК5 — Водность |
231 |
116 |
115 |
6.112 |
38.083 |
78 |
27 |
|
БПК5 — Zn |
173 |
93 |
80 |
6.079 |
0.046 |
77 |
21 |
|
БПК5 — Cr |
9 |
0 |
9 |
3.600 |
0.005 |
100 |
100 |
|
БПК5 — Пестициды |
110 |
64 |
46 |
5.341 |
0.083 |
80 |
17 |
|
БПК5 — Температура |
77 |
46 |
31 |
5.642 |
12.722 |
100 |
6 |
|
NH4 — NO2 |
231 |
116 |
115 |
0.965 |
0.208 |
75 |
44 |
|
NH4 — Нефтепродукты |
231 |
116 |
115 |
0.965 |
0.739 |
75 |
48 |
|
NH4 — Фенолы |
231 |
116 |
115 |
0.965 |
0.012 |
75 |
37 |
|
NH4 — СПАВ |
231 |
116 |
115 |
0.965 |
0.144 |
75 |
44 |
|
NH4 — Сu |
225 |
114 |
111 |
0.965 |
0.018 |
75 |
38 |
|
NH4 — Водность |
231 |
116 |
115 |
1.390 |
38.083 |
75 |
45 |
|
NH4 — Zn |
173 |
93 |
80 |
0.912 |
0.046 |
76 |
48 |
|
NH4 — Cr |
9 |
0 |
9 |
0.180 |
0.005 |
100 |
100 |
|
NH4 — Пестициды |
110 |
64 |
46 |
1.972 |
0.088 |
86 |
13 |
|
NH4 — Температура |
77 |
46 |
31 |
1.902 |
12.722 |
76 |
42 |
|
NO2 — Нефтепродукты |
231 |
116 |
115 |
0.203 |
0.628 |
75 |
35 |
|
NO2 — Фенолы |
231 |
116 |
115 |
0.203 |
0.009 |
75 |
21 |
|
NO2 — Cu |
225 |
114 |
111 |
0.216 |
0.016 |
76 |
23 |
|
NO2 — Водность |
231 |
116 |
115 |
0.216 |
81.444 |
78 |
16 |
|
NO2 — Zn |
173 |
93 |
80 |
0.203 |
0.096 |
76 |
16 |
|
NO2 — Cr |
9 |
0 |
9 |
0.071 |
0.005 |
100 |
100 |
|
NO2 — Пестициды |
110 |
64 |
46 |
0.210 |
0.083 |
77 |
22 |
|
NO2 — Температура |
77 |
46 |
31 |
0.526 |
12.722 |
100 |
6 |
|
Нефтепродукты — Фенолы |
231 |
116 |
115 |
0.567 |
0.010 |
76 |
38 |
|
Нефтепродукты — СПАВ |
231 |
116 |
115 |
0.741 |
0.106 |
77 |
29 |
|
Нефтепродукты — Cu |
225 |
114 |
111 |
0.596 |
0.045 |
76 |
31 |
|
Нефтепродукты — Водность |
231 |
116 |
115 |
0.741 |
138.083 |
75 |
35 |
|
Нефтепродукты — Zn |
173 |
93 |
80 |
0.741 |
0.096 |
78 |
23 |
|
Cu — Cr |
9 |
0 |
9 |
0.005 |
0.005 |
100% |
100% |
|
Cu — Пестициды |
110 |
64 |
46 |
0.016 |
0.058 |
78% |
30% |
|
Cu — Температура |
72 |
45 |
27 |
0.045 |
12.722 |
100% |
7% |
|
Водность — Zn |
173 |
93 |
80 |
193.652 |
0.096 |
86% |
7% |
|
Водность — Cr |
9 |
0 |
9 |
130.000 |
0.005 |
100% |
100% |
|
Водность — Пестициды |
110 |
64 |
46 |
133.913 |
0.083 |
86% |
13% |
|
Водность — Температура |
77 |
46 |
31 |
130.000 |
12.722 |
100% |
3% |
|
Zn — Cr |
0 |
0 |
0 |
0.000 |
0.000 |
100% |
0% |
|
Zn — Пестициды |
102 |
60 |
42 |
0.083 |
0.083 |
80% |
10% |
|
Zn — Температура |
72 |
45 |
27 |
0.083 |
12.722 |
80% |
15% |
|
Cr — Пестициды |
0 |
0 |
0 |
0.000 |
0.000 |
80% |
0% |
|
Cr — Температура |
0 |
0 |
0 |
0.000 |
0.000 |
80% |
0% |
|
Пестициды — Температура |
50 |
38 |
12 |
0.087 |
12.722 |
100% |
17% |
Таблица
12. Экологически допустимые уровни (ЭДУ) и экологически безопасные границы (ЭБГ) абиотических переменных экосистем бассейна Дона (обозначения в конце таблицы)|
Физико-химические переменные |
Планктон и перифитон |
Зообентос |
Судак и берш, уловы |
Лещ, уловы |
Чехонь, уловы |
Лещ и осетр, урожайность |
Наиболее жесткие ЭДУ или ЭБГ |
|
#Кислород |
6.955 |
8.07 |
9.569 |
9.663 |
9.938 |
8.908 |
9.938 |
|
#Взвешенные вещества |
7.273 |
6.564 |
5.21 |
2.16 |
1.885 |
7.273 |
1.885 |
|
#ХПК |
54.848 |
42.924 |
20.36 |
20.36 |
20.36 |
17.813 |
17.813 |
|
#Азот аммонийный |
2.25 |
0.75 |
0.768 |
0.544 |
0.299 |
0.778 |
0.299 |
|
# Азот аммонийный- |
0.01 |
0.01 |
0.027 |
0.027 |
0.125 |
0.241 |
0.241 |
|
#Азот нитритный |
0.205 |
0.108 |
0.132 |
0.045 |
0.008 |
0.032 |
0.008 |
|
#Азот нитратный |
2.832 |
1.179 |
0.31 |
0.49 |
0.175 |
1.658 |
0.175 |
|
# Азот нитратный- |
0.01 |
0.01 |
0.01 |
0.01 |
0.01 |
0.899 |
0.899 |
|
#Фосфор |
0.482 |
0.138 |
0.071 |
0.082 |
0.07 |
0.171 |
0.07 |
|
#Фосфор- |
0.007 |
0.017 |
0.024 |
0.024 |
0.065 |
0.062 |
0.065 |
|
#Нефтепродукты |
1.32 |
0.839 |
1.186 |
1.143 |
0.167 |
0.914 |
0.167 |
|
#Фенолы |
0.174 |
0.218 |
0.218 |
8.696 |
0.218 |
0.002 |
0.002 |
|
#СПАВ |
0.2 |
0.133 |
0.15 |
0.141 |
0.069 |
0.022 |
0.022 |
|
#Медь |
0.017 |
0.011 |
0.006 |
0.006 |
0.004 |
0.006 |
0.004 |
|
#Цинк |
0.036 |
0.01 |
0.006 |
0.008 |
0.002 |
0.002 |
0.002 |
|
#Железо |
2.625 |
1.39 |
2.237 |
2.237 |
0.215 |
1.07 |
0.215 |
|
#Железо- |
0.06 |
0.078 |
0.03 |
0.008 |
0.075 |
0.202 |
0.202 |
|
#a -ГХЦГ |
0.11 |
0.014 |
0.064 |
0.064 |
0.01 |
0.002 |
0.002 |
|
#g -ГХЦГ |
0.075 |
0.011 |
0.001 |
0.004 |
0.004 |
0.007 |
0.001 |
|
ДДЭ |
0.055 |
0.002 |
0.003 |
0.003 |
0.003 |
0.002 |
0.002 |
|
ДДТ |
0.74 |
0.02 |
0.103 |
0.103 |
0.103 |
0.74 |
0.02 |
|
#Сульфаты |
1015.075 |
878.125 |
1031.773 |
879.339 |
93.4 |
195.072 |
93.4 |
|
#Сульфаты- |
75.7 |
76 |
72.582 |
72.582 |
75.49 |
103.9 |
103.9 |
|
#Хлориды |
575.474 |
419.603 |
1484.566 |
386.413 |
48.506 |
399.1 |
48.506 |
|
#Кальций |
152.275 |
135.325 |
219.54 |
134.39 |
43.473 |
94.233 |
43.473 |
|
#Кальций- |
39.88 |
39.88 |
39.88 |
39.88 |
41.528 |
80.758 |
80.758 |
|
#Минерализация |
2469 |
2080.216 |
3747.5 |
2098.525 |
416.562 |
839.588 |
416.562 |
|
#Магний |
135.014 |
111.647 |
413.34 |
96.383 |
29.208 |
32.894 |
19.208 |
|
#Магний- |
26.518 |
23.02 |
14.05 |
14.05 |
22.796 |
26.94 |
26.94 |
|
#Марганец |
0.597 |
0.152 |
0.475 |
0.169 |
0 |
0 |
0 |
|
#Марганец- |
0.113 |
0.127 |
0.176 |
0.176 |
0 |
0.107 |
0.176 |
|
*Кислород |
4.028 |
5.246 |
4.95 |
4.95 |
5.057 |
8.206 |
8.206 |
|
*Взвешенные вещества |
6.106 |
5.657 |
5.508 |
2.105 |
1.903 |
0.345 |
0.345 |
|
* ХПК |
102.792 |
82.85 |
35.325 |
36.5 |
36.5 |
31.492 |
31.492 |
|
*Азот аммонийный |
1.938 |
1.563 |
1.552 |
1.631 |
0.674 |
0.119 |
0.119 |
|
*Азот нитритный |
0.445 |
0.332 |
0.49 |
0.274 |
0.021 |
0.048 |
0.021 |
|
*Азот нитратный |
6.8 |
6.8 |
0.804 |
0.804 |
0.36 |
6.8 |
0.36 |
|
*Фосфор |
1.44 |
0.9 |
0.203 |
0.25 |
0.192 |
0.254 |
0.192 |
|
*Нефтепродукты |
2.096 |
3.072 |
2.914 |
2.819 |
0.885 |
0.355 |
0.355 |
|
*Фенолы |
0.15 |
0.031 |
0.018 |
0.015 |
0.005 |
0.006 |
0.005 |
|
*СПАВ |
0.6 |
0.368 |
0.231 |
0.173 |
0.192 |
0.035 |
0.035 |
|
*Медь |
0.14 |
0.043 |
0.019 |
0.02 |
0.013 |
0.005 |
0.005 |
|
*Цинк |
0.046 |
0.037 |
0.015 |
0.018 |
0.015 |
0.003 |
0.003 |
|
*Железо |
9.6 |
3.12 |
11.071 |
11.071 |
0.59 |
0.749 |
0.59 |
|
*a -ГХЦГ |
0.112 |
0.025 |
0.064 |
0.064 |
0.018 |
0.007 |
0.007 |
|
*g -ГХЦГ |
0.093 |
0.039 |
0.008 |
0.009 |
0.009 |
0.018 |
0.008 |
|
ДДЭ |
0.047 |
0.012 |
0.018 |
0.018 |
0.018 |
0.012 |
0.012 |
|
ДДТ |
0.122 |
0.74 |
0.64 |
0.938 |
0.938 |
0.03 |
0.03 |
|
*Сульфаты |
1416.506 |
1000.478 |
1889.765 |
1919.73 |
131.88 |
196.313 |
131.88 |
|
*Хлориды |
1096.952 |
886.9 |
5891.235 |
523.303 |
65.96 |
881 |
65.96 |
|
*Кальций |
188.55 |
161.1 |
417.6 |
175.995 |
52.745 |
133.193 |
52.745 |
|
*Минерализация |
3066.288 |
2983 |
9891.375 |
2819.37 |
913 |
1194.28 |
913 |
|
*Магний |
196.776 |
137.695 |
871.8 |
122.363 |
15.93 |
91.5 |
15.93 |
|
*Марганец |
2.05 |
0.225 |
0.76 |
0.667 |
0 |
0 |
0 |
|
В-1 |
1.992 |
1.509 |
1.097 |
1.394 |
1.108 |
1.992 |
1.097 |
|
В-1- |
0.447 |
0.664 |
0.8 |
0.8 |
0.8 |
1.147 |
1.147 |
|
В-2 |
2.493 |
2.493 |
1.111 |
1.22 |
1.091 |
2.493 |
1.091 |
|
В-2- |
0.453 |
0.5 |
0.444 |
0.786 |
0.805 |
1.139 |
1.139 |
|
В-3 |
2.075 |
1.945 |
0.964 |
1.173 |
1.023 |
0.379 |
0.379 |
|
В-3- |
0.369 |
0.48 |
0.894 |
0.743 |
0.743 |
2.091 |
2.091 |
|
В-4 |
3.708 |
2.065 |
1.138 |
1.341 |
0.925 |
3.708 |
0.925 |
|
В-4- |
0.595 |
0.595 |
0.767 |
0.767 |
0.761 |
1.2 |
1.2 |
|
В-5 |
2.635 |
2.599 |
1.243 |
1.283 |
0.93 |
2.915 |
0.93 |
|
В-5- |
0.723 |
0.664 |
0.744 |
0.744 |
0.816 |
1.6 |
1.6 |
|
В-6 |
1.411 |
1.159 |
1.105 |
1.288 |
0.992 |
0.544 |
0.544 |
|
В-6- |
1.036 |
0.778 |
0.794 |
0.724 |
0.794 |
2.028 |
2.028 |
|
В-7 |
2.147 |
1.407 |
1.125 |
1.136 |
1.057 |
2.147 |
1.057 |
|
В-7- |
0.421 |
0.841 |
0.899 |
0.705 |
0.705 |
0.971 |
0.971 |
|
В-8 |
2.362 |
1.265 |
1.117 |
1.117 |
1.032 |
1.773 |
1.032 |
|
В-8- |
0.391 |
0.994 |
0.895 |
0.694 |
0.694 |
1.13 |
1.13 |
|
В-9 |
2.09 |
1.298 |
1.057 |
1.077 |
1.057 |
1.021 |
1.021 |
|
В-9- |
0.506 |
0.625 |
0.927 |
0.743 |
0.743 |
2.051 |
2.051 |
|
В-10 |
1.705 |
1.123 |
1.13 |
1.152 |
0.905 |
1.705 |
0.905 |
|
В-10- |
0.579 |
0.648 |
0.875 |
0.684 |
0.698 |
1.02 |
1.02 |
|
В-11 |
2.012 |
1.151 |
1.103 |
1.103 |
0.888 |
2.012 |
0.888 |
|
В-11- |
0.537 |
0.537 |
0.882 |
0.719 |
0.719 |
1.07 |
1.07 |
|
В-12 |
1.017 |
0.988 |
1.106 |
1.106 |
0.974 |
0.573 |
0.573 |
|
В-12- |
1.046 |
0.988 |
0.872 |
0.731 |
0.731 |
2.155 |
2.155 |
|
#Водность |
2.255 |
1.361 |
1.346 |
1.291 |
0.969 |
2.255 |
0.969 |
|
#Водность- |
0.401 |
0.374 |
0.348 |
0.355 |
0.832 |
1.334 |
1.334 |
|
Т-1 |
5.947 |
1.212 |
0.191 |
1.852 |
1.852 |
5.947 |
0.191 |
|
Т-1- |
0.028 |
0.176 |
1.809 |
0.148 |
1.809 |
1.064 |
1.809 |
|
Т-2 |
3.629 |
2.468 |
1.818 |
0.238 |
0.182 |
1.476 |
0.182 |
|
Т-2- |
0.056 |
0.058 |
0.968 |
0.147 |
1.818 |
0.309 |
1.818 |
|
Т-3 |
2.82 |
2.64 |
1.027 |
1.515 |
1.212 |
0.631 |
0.631 |
|
Т-3- |
0.048 |
0.11 |
0.985 |
0.965 |
1.48 |
0.22 |
1.48 |
|
Т-4 |
1.587 |
1.024 |
1.243 |
1.585 |
1.089 |
1.029 |
1.024 |
|
Т-4- |
0.497 |
0.673 |
0.506 |
0.47 |
1.071 |
0.735 |
1.071 |
|
Т-5 |
0.982 |
0.976 |
1.141 |
1.161 |
1.102 |
0.958 |
0.958 |
|
Т-5- |
0.836 |
0.654 |
0.731 |
0.731 |
1.122 |
0.894 |
1.122 |
|
Т-6 |
1.157 |
1.019 |
1.056 |
1.056 |
1.056 |
1.161 |
1.019 |
|
Т-6- |
0.655 |
0.806 |
0.892 |
0.907 |
1.017 |
0.969 |
1.017 |
|
Т-7 |
1.211 |
1.163 |
1.143 |
1.163 |
0.913 |
1.005 |
0.913 |
|
Т-7- |
0.902 |
0.881 |
0.902 |
0.857 |
0.886 |
0.905 |
0.905 |
|
Т-8 |
1.113 |
1.106 |
1.116 |
1.247 |
1.151 |
1.007 0 |
1.007 |
|
Т-8- |
0.958 |
0.966 |
0.921 |
0.959 |
0.996 |
0.972 |
0.996 |
|
Т-9 |
1.294 |
1.094 |
1.093 |
1.214 |
0.982 |
1.046 |
0.982 |
|
Т-9- |
0.93 |
0.926 |
0.941 |
0.941 |
0.99 |
0.999 |
0.999 |
|
Т-10 |
1.305 |
1.162 |
1.407 |
1.168 |
1.03 |
1.209 |
1.03 |
|
Т-10- |
0.717 |
0.768 |
0.726 |
0.755 |
1.021 |
0.831 |
1.021 |
|
Т-11 |
1.625 |
1.556 |
1.351 |
1.511 |
1.298 |
0.955 |
0.955 |
|
Т-11- |
0.179 |
0.386 |
0.944 |
0.844 |
1.091 |
0.401 |
1.091 |
|
Т-12 |
2.492 |
2.431 |
1.401 |
1.401 |
0.79 |
2.492 |
0.79 |
|
Т-12- |
0.089 |
0.101 |
0.462 |
0.28 |
0.476 |
1.021 |
1.021 |
|
#Температура |
1.369 |
1.193 |
1.222 |
1.192 |
1.005 |
0.967 |
0.967 |
|
#Температура- |
0.755 |
0.81 |
0.809 |
0.891 |
0.928 |
0.88 |
0.928 |
|
рН-1 |
8.221 |
8.031 |
8.21 |
8.21 |
8.21 |
7.852 |
7.852 |
|
рН-1- |
7.574 |
7.718 |
7.575 |
7 |
7 |
7.823 |
7.823 |
|
рН-2 |
8.2 |
8.05 |
8.5 |
8.238 |
7.83 |
7.65 |
7.65 |
|
рН-2- |
6.02 |
7 |
7 |
7 |
7 |
7.45 |
7.45 |
|
рН-3 |
8.228 |
8.21 |
8.23 |
8.23 |
7.807 |
8.006 |
7.807 |
|
рН-3- |
6.5 |
7.654 |
7.63 |
7.63 |
7.629 |
7.989 |
7.989 |
|
рН-4 |
8.399 |
8.331 |
8.7 |
8.425 |
7.62 |
8.208 |
7.62 |
|
рН-4- |
7.16 |
7.21 |
7.21 |
7.21 |
7.21 |
8.188 |
8.188 |
|
рН-5 |
8.208 |
8.22 |
8.4 |
8.4 |
8.4 |
8.3 |
8.208 |
|
рН-5- |
6 |
6.96 |
7.58 |
7.58 |
8.222 |
8.19 |
8.222 |
|
рН-6 |
8.4 |
8.21 |
8.22 |
8.4 |
8.4 |
8.073 |
8.073 |
|
рН-6- |
7.92 |
6.03 |
6.03 |
6.03 |
8.163 |
7.987 |
8.163 |
|
рН-7 |
8.16 |
8.05 |
8.4 |
8.4 |
7.901 |
8.2 |
7.901 |
|
рН-7- |
7.734 |
7.864 |
7.592 |
7.59 |
7.59 |
8.03 |
8.03 |
|
рН-8 |
8.23 |
8.214 |
8.39 |
8.211 |
7.612 |
8.205 |
7.612 |
|
рН-8- |
6 |
7.59 |
7.09 |
7.09 |
7.09 |
8.189 |
8.189 |
|
рН-9 |
8.304 |
8.22 |
8.294 |
8.4 |
7.635 |
8.186 |
7.635 |
|
рН-9- |
7.584 |
7.01 |
7.01 |
7.01 |
7.01 |
8.168 |
8.168 |
|
рН-10 |
8.81 |
8.81 |
8.406 |
8.81 |
8.81 |
8.2 |
8.2 |
|
рН-10- |
6.5 |
6.5 |
7.09 |
7.09 |
7.453 |
8.171 |
8.171 |
|
рН-11 |
8.227 |
8.108 |
8.25 |
8.25 |
7.653 |
8.103 |
7.653 |
|
рН-11- |
7.462 |
5.98 |
7.59 |
5.98 |
7.593 |
8.015 |
8.015 |
|
рН-12 |
8.23 |
8.21 |
8.23 |
8.23 |
7.831 |
8.23 |
7.831 |
|
рН-12- |
7.001 |
7.795 |
7.6 |
7.6 |
7.6 |
7.847 |
7.847 |
|
#pH |
8.127 |
8.093 |
8.264 |
8.172 |
7.694 |
8.093 |
7.694 |
|
#pH- |
6.5 |
6.933 |
7.626 |
7.626 |
7.641 |
8.025 |
8.025 |
|
#БПК5 |
5.513 |
5.496 |
5.901 |
5.901 |
3.728 |
3.001 |
3.001 |
|
*БПК5 |
14.14 |
13.221 |
12.616 |
12.528 |
12.52 |
3.854 |
3.854 |
Примечание: жирным шрифтом выделены значения экологически допустимых уровней (ЭДУ); обычным шрифтом обозначены значения экологически безопасных границ (ЭБГ); # — среднегодовые значения; * — наихудшие значения за год; значок "-" после переменной — ЭДУ ищется в области малых значений переменной; B-N — среднемесячное значение водности за месяц с номером N; T-N — среднемесячное значение относительной температуры воды за месяц с номером N; pH-N — среднемесячные значения водородного показателя за месяц с номером N; пестициды измерены в мкг/л, остальные вещества — в мг/л; водность, относительная температура и взвешенные вещества безразмерны.
Таблица 13. Значения ЭДУ значимых факторов бассейна Дона, вычисленные для разных биотических идентификаторов
|
Абиотический фактор |
ЭДУ |
Точность, % |
Полнота, % |
|
Планктон и перифитон |
|||
|
Температура (май), в.у. |
0.982 |
82 |
85 |
|
Водность (июнь), н.у. |
1.036 |
81 |
55 |
|
Водность (май), н.у. |
0.723 |
81 |
52 |
|
pH (июль) н.у. |
7.73 |
86 |
48 |
|
pH (июнь) н.у. |
7.92 |
80 |
35 |
|
g - ГХЦГ макс. |
0.093 |
100 |
31 |
|
Температура (сентябрь), н.у. |
0.930 |
86 |
30 |
|
Кислород мин. |
4.03 |
83 |
18 |
|
Суммарные точность и полнота |
76 |
96 |
|
|
Зообентос |
|||
|
Температура (май), в.у. |
0.976 |
80 |
80 |
|
Водность (май), н.у. |
0.664 |
92 |
55 |
|
pH (июль) н.у. |
7.86 |
80 |
63 |
|
g - ГХЦГ макс. |
0.039 |
92 |
55 |
|
Кислород мин. |
5.25 |
80 |
24 |
|
ДДЭ сред. |
0.002 |
81 |
87 |
|
Температура (апрель), в.у. |
1.024 |
81 |
65 |
|
Температура (июнь), в.у. |
1.019 |
81 |
76 |
|
g - ГХЦГ сред. |
0.011 |
86 |
57 |
|
ДДЭ макс. |
0.012 |
86 |
80 |
|
Водность (август), н.у. |
0.994 |
80 |
75 |
|
pH (март), н.у. |
7.65 |
82 |
56 |
|
a - ГХЦГ макс. |
0.025 |
80 |
42 |
|
pH (январь), н.у. |
7.72 |
80 |
47 |
|
Температура (апрель), н.у. |
0.673 |
86 |
43 |
|
Цинк сред. |
0.01 |
83 |
28 |
|
Температура (январь), н.у. |
0.176 |
83 |
71 |
|
Азот нитратный сред., в.у. |
1.179 |
83 |
22 |
|
Водность (средняя за год), в.у. |
1.361 |
83 |
24 |
|
Температура (сентябрь), в.у. |
1.094 |
80 |
27 |
|
Температура (октябрь), в.у. |
1.162 |
80 |
22 |
|
Суммарные точность и полнота |
76 |
97 |
|
|
Уловы судака и берша |
|||
|
Цинк сред. |
0.016 |
83 |
38 |
|
ХПК сред. |
20.5 |
86 |
75 |
|
ХПК макс. |
40.1 |
80 |
50 |
|
Суммарные точность и полнота |
79 |
85 |
|
|
Уловы леща |
|||
|
Азот нитритный сред. |
0.045 |
89 |
67 |
|
Взвешенные вещества макс. |
2.105 |
83 |
36 |
|
pH (средний за год), в.у. |
8.17 |
83 |
62 |
|
Суммарные точность и полнота |
80 |
86 |
|
|
Уловы чехони |
|||
|
Азот нитратный сред., в.у. |
0.175 |
80 |
57 |
|
Водность (средняя за год), в.у. |
0.969 |
80 |
57 |
|
Азот нитритный сред. |
0.008 |
81 |
93 |
|
Медь макс. |
0.013 |
83 |
71 |
|
Азот нитратный макс. |
0.36 |
82 |
90 |
|
Водность (май), в.у. |
0.93 |
88 |
88 |
|
Водность (октябрь), в.у. |
0.905 |
80 |
89 |
|
Водность (ноябрь), в.у. |
0.888 |
80 |
100 |
|
pH (апрель), в.у. |
7.62 |
80 |
100 |
|
БПК 5 сред. |
3.73 |
80 |
80 |
|
Медь сред. |
0.004 |
88 |
78 |
|
Суммарные точность и полнота |
78 |
100 |
|
|
Урожайность леща и осетра |
|||
|
Кислород мин. |
6.51 |
80 |
65 |
|
a - ГХЦГ макс. |
0.013 |
90 |
73 |
|
g - ГХЦГ сред. |
0.002 |
83 |
100 |
|
pH (март), н.у. |
7.9 |
80 |
55 |
|
Азот нитритный макс. |
0.111 |
80 |
86 |
|
Фенолы макс. |
0.01 |
81 |
78 |
|
pH (май), н.у. |
8.17 |
90 |
86 |
|
Сульфаты сред., в.у. |
195 |
85 |
58 |
|
Цинк макс. |
0.023 |
80 |
33 |
|
Сульфаты макс. |
196 |
83 |
100 |
|
Суммарные точность и полнота |
77 |
100 |
|
Примечание: в.у. — верхний уровень; н.у. — нижний уровень; макс. — максимальное значение за год; мин. — минимальное значение за год; сред. — среднесезонное значение. Температура выражена в долях от среднемноголетнего значения, пестициды в мкг/л, остальные абиотические переменные — в мг/л (или безразмерны).
Таблица 14
. Существенность переменных, значимых для планктона и перифитона в бассейне Дона. в.у. — верхний уровень, н.у. - нижний уровень. макс. - максимальное значение за год|
Шаг |
Переменные |
Достигаемые суммарные |
Существенность, % |
|
|
точность,% |
полнота, % |
|||
|
1 |
Температура (май), в.у. |
82 |
85 |
40 |
|
2 |
pH (июль), н.у. Кислород мин. |
82 81 |
76 54 |
14 12 |
|
3 |
Кислород мин. g -ГХЦГ макс.Температура (сентябрь), н.у. Водность (май), н.у. Водность (июнь), н.у. pH (июнь), н.у. |
81 82 80 79 77 77 |
59 72 77 79 79 79 |
5 3 3 3 3 3 |
|
4 |
Температура (сентябрь), н.у. |
80 |
62 |
3 |
|
5 |
g -ГХЦГ макс.Водность (май), н.у. Водность (июнь), н.у. pH (июнь), н.у. |
80 77 76 76 |
64 64 64 64 |
2 2 2 2 |
|
6 |
Водность (май), н.у. Водность (июнь), н.у. pH (июнь), н.у. |
78 76 76 |
66 66 66 |
2 2 2 |
Таблица 15
. Учет сопряженности низкой численности зоопланктона с несколькими объясняющими факторами в р. Суре путем конструирования вторичной переменной|
Объясняющая переменная |
Точность сопряженности с низкой численностью зоопланктона |
Полнота сопряженности с низкой численностью зоопланктона |
|
Взвешенные вещества (несоблюдение ЭДУ) |
83 |
29 |
|
pH (несоблюдение ЭДУ) |
60 |
47 |
|
NH4 (несоблюдение ЭДУ) |
62 |
48 |
|
NO2 (несоблюдение ЭДУ) |
59 |
52 |
|
Взвешенные вещества + pH (несоблюдение ЭДУ хотя бы по одному из факторов) |
95 |
60 |
|
Взвешенные вещества + pH + +NH4 (несоблюдение ЭДУ хотя бы по одному из факторов) |
58 |
81 |
|
Взвешенные вещества + pH + + NH4 + NO2 (несоблюдение ЭДУ хотя бы по одному из факторов) |
54 |
92 |
Таблица 16.
Сравнение ЭДУ факторов среды в р. Суре, вычисленных для различных периодов исследования (в.у. — верхний уровень, н.у. — нижний уровень)|
Физико-химический |
Значение ЭДУ для численности суммарного зоопланктона |
||
|
показатель |
Контекст “1993-1995 гг.” |
Контекст “1996-1997 гг.” |
1993-1997 гг. |
|
БПК (в.у.), мг/л |
2.72 |
8.8 |
4.48 |
|
Fe (в.у.), мг/л |
0.84 |
0.84 |
0.84 |
|
O2 (н.у.), мг/л |
10.7 |
4.8 |
5.28 |
|
Mn (в.у.), мг/л |
0.07 |
0.06 |
0.07 |
|
NH4 (н.у.; в.у.), мг/л |
0.2-0.63 |
0.13-1.28 |
0.2-1.28 |
|
NO2 (н.у.; в.у.), мг/л |
0.04-0.12 |
0.04-0.08 |
0.04-0.2 |
|
NO3 (н.у.; в.у.), мг/л |
0.02-0.75 |
0.03-0.59 |
0.02-0.82 |
|
Углеводороды (в.у.), мг/л |
0.02 |
0.12 |
0.45 |
|
pH |
7.76-9.56 |
7.35-8.25 |
7.75-9.56 |
|
Фенолы (в.у.), мг/л |
0.0019 |
0.0034 |
0.0038 |
|
PO4 (н.у.; в.у.), мг/л |
0.06-0.24 |
0-0.31 |
0-0.27 |
|
Взвешенные вещества (в.у.), мг/л |
11.5 |
16.5 |
16.5 |
Таблица 17.
Средние, среднеквадратичные и коэффициенты вариации ЭДУ в бассейне Дона, полученные методом “бутстрэп” (в.у. — верхний уровень, н.у. — нижний уровень)|
Переменная |
ЭДУ m |
ЭДУ s |
ЭДУ v |
|
O2 (н.у.) |
4.32 |
1.35 |
31 |
|
g -гексахлорциклогексан (в.у.) |
0.076 |
0.015 |
19 |
|
относительная температура в сентябре (н.у.) |
0.95 |
0.015 |
2 |
|
водность в мае (н.у.) |
0.89 |
0.39 |
43 |
|
водность в июне (н.у.) |
1.3 |
0.53 |
41 |
|
относительная температура в мае (в.у.) |
1.03 |
0.17 |
16 |
|
pH в июне (н.у.) |
7.37 |
0.94 |
13 |
|
pH в июле (н.у.) |
7.53 |
0.31 |
4 |
Таблица 18.
Значения ЭДУ (выделены шрифтом) и ЭБГ физико-химических переменных для разных бассейнов и подбассейнов европейской части бывшего СССР, вычисленные по показателям организмов водной толщи и грунтов|
Физико-химические переменные |
Западная Двина |
Неман |
Дунай |
Днестр |
Днепр |
Волга |
Верхняя Волга |
Средняя Волга |
Нижняя Волга |
Дон |
ПДК |
||||
|
грунты |
грунты |
толща |
толща |
толща |
толща |
грунты |
грунты |
толща |
грунты |
толща |
грунты |
толща |
грунты |
||
|
NH4 средние, мг/л |
0.1 |
0.38 |
0.05 |
1.05 |
2.56 |
0.68 |
0.52 |
0.36 |
0.68 |
0.52 |
0.12 |
0.12 |
0.39 |
||
|
Cr средний, мг/л |
0.002 |
0.02 |
|||||||||||||
|
Cu средняя, мг/л |
0.013 |
0.01 |
0.012 |
0.009 |
0.02 |
0.02 |
0.02 |
0.006 |
0.02 |
0.02 |
0.017 |
0.017 |
0.001 |
||
|
Нефтепродукты средние, мг/л |
0.51 |
0.52 |
0.22 |
0.13 |
0.47 |
0.63 |
0.51 |
0.56 |
0.63 |
0.21 |
0.43 |
0.43 |
0.05 |
||
|
Zn средний, мг/л |
0.063 |
0.035 |
0.02 |
0.028 |
0.069 |
0.069 |
0.024 |
0.069 |
0.069 |
0.058 |
0.054 |
0.01 |
0.01 |
||
|
Взвешенные вещества средние, мг/л |
16.8 |
128 |
153 |
51 |
51 |
13 |
18.8 |
18.8 |
51 |
51 |
0.25 |
||||
|
Пестициды средние, мкг/л |
0.006 |
0.94 |
0.12 |
0.199 |
0.062 |
0.199 |
0.062 |
0.115 |
0.058 |
||||||
|
БПК 5 среднее, мг/л |
3.15 |
4.31 |
4.6 |
4.48 |
4.57 |
4.65 |
4.65 |
2.85 |
3.47 |
3.47 |
4.65 |
4.65 |
3 |
||
|
P средний, мг/л |
0.033 |
0.113 |
0.29 |
1.167 |
0.301 |
0.225 |
0.225 |
0.225 |
0.198 |
0.198 |
0.066 |
0.081 |
|||
|
NO2 средние, мг/л |
0.022 |
0.11 |
0.05 |
0.39 |
0.064 |
0.053 |
0.086 |
0.011 |
0.086 |
0.086 |
0.059 |
0.059 |
0.02 |
||
|
СПАВ средние, мг/л |
0.019 |
0.02 |
0.2 |
0.08 |
0.08 |
0.08 |
0.08 |
0.08 |
0.06 |
0.06 |
0.1 |
||||
|
Фенолы средние, мг/л |
0.007 |
0.007 |
0.006 |
0.007 |
0.005 |
0.015 |
0.015 |
0.008 |
0.015 |
0.015 |
0.005 |
0.005 |
0.001 |
||
|
NO3 средние, мг/л |
2.02 |
0.055 |
1.5 |
4.33 |
0.74 |
2 |
0.81 |
2 |
2 |
0.74 |
0.83 |
9.1 |
|||
|
ХПК среднее, мг/л |
38.8 |
34 |
69.1 |
52 |
35.4 |
35.4 |
29.8 |
22.5 |
22.5 |
24 |
34.5 |
||||
|
Ni средний, мг/л |
0.026 |
0.013 |
0.01 |
||||||||||||
|
Fe среднее, мг/л |
0.51 |
0.26 |
0.52 |
0.52 |
0.47 |
0.52 |
0.52 |
0.5 |
|||||||
|
Кислород минимальный, мг/л |
4.03 |
5.25 |
4 |
||||||||||||
|
a -ГХЦГ максимальный, мг/л |
0.025 |
0.02 |
|||||||||||||
|
g -ГХЦГ средний, мг/л |
0.011 |
0.02 |
|||||||||||||
|
g -ГХЦГ максимальный, мг/л |
0.093 |
0.039 |
0.02 |
||||||||||||
|
ДДЭ средний, мг/л |
0.002 |
||||||||||||||
|
ДДЭ максимальный, мг/л |
0.012 |
||||||||||||||
Таблица 19
. Значения ЭДУ (выделены шрифтом) и ЭБГ физико-химических переменных для разных бассейнов и подбассейнов азиатской части бывшего СССР, вычисленные по показателям организмов водной толщи|
Физико-химические переменные |
Обь (район КАТЭК) |
Обь (подбассейн Иртыша) |
Енисей (район Забайкалья) |
Енисей (подбассейн Ангары) |
Енисей (подбассейн Верхнего Енисея) |
Енисей в целом |
Лена |
Амур (подбассейн Амура) |
Амур (подбассейн Уссури) |
Амур в целом |
Сырдарья |
ПДК |
|
БПК 5 среднее, мг/л |
0.637 |
1.96 |
2.61 |
3.6 |
2.747 |
1.408 |
6.485 |
3.736 |
4.234 |
3.79 |
3 |
|
|
БПК 5 максимальное, мг/л |
2.677 |
5.213 |
45 |
14 |
5.123 |
3.93 |
13.212 |
9.711 |
10.774 |
3 |
||
|
ХПК среднее, мг/л |
23.9 |
21.069 |
25.903 |
24.245 |
||||||||
|
ХПК максимальное, мг/л |
44 |
61.253 |
82.267 |
70.359 |
||||||||
|
pH среднее |
7.95 |
7.79 |
7.216 |
8.5 |
||||||||
|
Минерализация средняя, мг/л |
541 |
1000 |
||||||||||
|
Фенолы средние, мг/л |
0.003 |
0.002 |
0.004 |
0.016 |
0.005 |
0.001 |
||||||
|
Фенолы максимальные, мг/л |
0.006 |
0.133 |
0.043 |
0.001 |
||||||||
|
Летучие фенолы средние, мг/л |
0.012 |
0.012 |
||||||||||
|
Летучие фенолы максимальные, мг/л |
0.015 |
0.015 |
||||||||||
|
Fe среднее, мг/л |
2.6 |
1.52 |
0.05 |
0.5 |
||||||||
|
Fe максимальное, мг/л |
2.76 |
6 |
7.48 |
7.48 |
0.5 |
|||||||
|
Cu среднее, мг/л |
0.006 |
0.011 |
0.003 |
0.118 |
0.118 |
0.006 |
0.001 |
|||||
|
Cu максимальное, мг/л |
0.01 |
0.051 |
0.016 |
0.188 |
0.19 |
0.19 |
0.001 |
|||||
|
Ni средний, мг/л |
0.007 |
0.027 |
0.01 |
|||||||||
|
Ni максимальный, мг/л |
0.166 |
0.166 |
0.021 |
0.08 |
0.01 |
|||||||
|
B средний, мг/л |
0.232 |
0.232 |
0.017 |
|||||||||
|
B максимальный, мг/л |
0.951 |
0.951 |
0.017 |
|||||||||
|
NO3 средние, мг/л |
0.733 |
0.2 |
0.33 |
0.33 |
0.366 |
2.33 |
9 |
|||||
|
NO3 максимальные, мг/л |
2.458 |
0.707 |
9 |
|||||||||
|
NO2 средние, мг/л |
0.021 |
0.007 |
0.015 |
0.114 |
0.061 |
0.04 |
0.033 |
0.039 |
0.048 |
0.02 |
||
|
NO2 максимальные, мг/л |
0.015 |
0.072 |
0.116 |
0.229 |
0.229 |
0.02 |
||||||
|
NH4 средние, мг/л |
0.212 |
0.384 |
0.04 |
0.568 |
0.057 |
1.261 |
1.758 |
1.72 |
0.18 |
0.39 |
||
|
NH4 максимальные, мг/л |
0.346 |
0.31 |
1.558 |
0.143 |
3.848 |
4.053 |
4.053 |
0.39 |
||||
|
O2 средний, мг/л |
4.09 |
6.89 |
5.8 |
7.2 |
8.803 |
5.8 |
8.616 |
7.08 |
4 |
|||
|
O2 минимальный, мг/л |
4.09 |
4.1 |
3.3 |
6.819 |
5.301 |
4 |
||||||
|
P средний, мг/л |
0.376 |
0.986 |
0.216 |
|||||||||
|
P максимальный, мг/л |
1.244 |
2.461 |
||||||||||
|
Zn средний, мг/л |
0.032 |
0.044 |
0.065 |
0.5 |
0.5 |
0.01 |
||||||
|
Zn максимальный, мг/л |
0.07 |
0.128 |
0.01 |
|||||||||
|
Cd средний, мг/л |
0.004 |
0.004 |
0.001 |
|||||||||
|
Cd максимальный, мг/л |
0.021 |
0.021 |
0.001 |
|||||||||
|
Pb максимальный, мг/л |
0.018 |
0.03 |
||||||||||
|
Mg средний, мг/л |
9.871 |
940 |
||||||||||
|
Mg максимальный, мг/л |
25.02 |
940 |
||||||||||
|
Ca средний, мг/л |
61.768 |
610 |
||||||||||
|
Ca максимальный, мг/л |
132.952 |
610 |
||||||||||
|
SO4 средние, мг/л |
54.24 |
89.996 |
100 |
|||||||||
|
SO4 максимальные, мг/л |
105.86 |
538.299 |
100 |
|||||||||
|
Cl средние, мг/л |
67.435 |
300 |
||||||||||
|
Cl максимальные, мг/л |
135.152 |
300 |
||||||||||
|
Cr средний, мг/л |
0.008 |
0.004 |
0.007 |
0.005 |
0.02 |
|||||||
|
Cr максимальный, мг/л |
0.015 |
0.02 |
0.02 |
|||||||||
|
Сумма ионов средняя |
396.859 |
|||||||||||
|
Сумма ионов максимальная |
288.701 |
|||||||||||
|
Нефтепродукты средние, мг/л |
1.256 |
0.8 |
0.59 |
0.193 |
0.093 |
0.15 |
0.05 |
|||||
|
Нефтепродукты максимальные, мг/л |
4.963 |
5.57 |
1.58 |
1.26 |
1.26 |
0.384 |
0.05 |
|||||
|
СПАВ средние, мг/л |
0.055 |
0.112 |
0.038 |
0.064 |
0.03 |
0.1 |
||||||
|
СПАВ максимальные, мг/л |
0.176 |
0.105 |
0.1 |
|||||||||
|
H2 S средний, мг/л |
0.061 |
0 |
||||||||||
|
Взвешенные вещества средние, мг/л |
118 |
37.37 |
46.6 |
841 |
||||||||
|
Взвешенные вещества максимальные, мг/л |
118 |
119.738 |
160 |
|||||||||
|
Лигнин средний, мг/л |
0.2 |
|||||||||||
|
Лигнин максимальный, мг/л |
1.5 |
|||||||||||
|
Линдан средний, мг/л |
0.026 |
0.026 |
||||||||||
|
Линдан максимальный, мг/л |
0.042 |
0.16 |
0.16 |
|||||||||
|
Лигносульфонат средний, мг/л |
0.616 |
0.616 |
||||||||||
|
Лигносульфонат максимальный, мг/л |
2.147 |
2.147 |
||||||||||
|
Цианиды средние, мг/л |
0.179 |
0.178 |
0.05 |
|||||||||
|
Цианиды максимальные, мг/л |
0.49 |
0.496 |
0.05 |
|||||||||
|
Роданиды средние, мг/л |
0.283 |
0.283 |
0.1 |
|||||||||
|
Роданиды максимальные, мг/л |
0.217 |
0.569 |
0.1 |
|||||||||
|
Альфа-ГХЦГ средний, мг/л |
0.038 |
0.038 |
0.002 |
0.002 |
0.02 |
|||||||
|
Альфа-ГХЦГ максимальный, мг/л |
0.084 |
0.084 |
0.004 |
0.004 |
0.02 |
|||||||
|
Гамма-ГХЦГ средний, мг/л |
0.041 |
0.041 |
0.002 |
0.002 |
0.02 |
|||||||
|
Гамма-ГХЦГ максимальный, мг/л |
0.083 |
0.083 |
0.004 |
0.004 |
0.02 |
|||||||
|
Гексахлоран средний, мг/л |
0.006 |
0.006 |
0 |
|||||||||
|
Гексахлоран максимальный, мг/л |
0.059 |
0 |
||||||||||
|
Пропанид средний, мг/л |
0.001 |
0.001 |
0.0003 |
|||||||||
|
Пропанид максимальный, мг/л |
0.003 |
0.003 |
0.0003 |
|||||||||
|
ДДТ среднее, мг/л |
0.54 |
0.54 |
0.1 |
|||||||||
|
ДДЭ среднее, мг/л |
0.01 |
0.01 |
||||||||||
|
ДДЭ максимальное, мг/л |
0.04 |
0.04 |
||||||||||
|
ДДД среднее, мг/л |
0.04 |
0.04 |
||||||||||
|
ДДД максимальное, мг/л |
0.3 |
0.3 |
||||||||||
|
Фториды максимальные, мг/л |
2.19 |
|||||||||||
|
Сатурн средний, мг/л |
0.05 |
0.0002 |
Таблица 20.
Значения ЭДУ (выделены шрифтом) и ЭБГ физико-химических переменных для разных бассейнов и подбассейнов азиатской части бывшего СССР, вычисленные по показателям организмов грунтов|
Физико-химические переменные |
Енисей (район Забайкалья) |
Енисей (подбассейн Ангары)г |
Енисей (подбассейн Верхнего Енисея) |
Енисей в целом |
Лена |
Амур (подбассейн Амура) |
Амур (подбассейн Уссури) |
Амур в целом |
ПДК |
|
БПК 5 среднее, мг/л |
2.61 |
3.6 |
2.747 |
1.408 |
9.224 |
3.736 |
37.6 |
3 |
|
|
БПК 5 максимальное, мг/л |
4.14 |
14 |
5.123 |
5.688 |
1.968 |
14.799 |
9.711 |
10.908 |
3 |
|
ХПК среднее, мг/л |
23.9 |
18.256 |
24.245 |
24.245 |
|||||
|
ХПК максимальное, мг/л |
34.16 |
68.4 |
79.877 |
||||||
|
pH среднее |
8 |
7.65 |
7.225 |
7.664 |
8.5 |
||||
|
Фенолы средние, мг/л |
0.002 |
0.003 |
0.04 |
0.014 |
0.07 |
0.001 |
|||
|
Фенолы максимальные, мг/л |
0.022 |
0.031 |
0.012 |
0.14 |
0.04 |
0.062 |
0.001 |
||
|
Летучие фенолы средние, мг/л |
0.004 |
0.004 |
|||||||
|
Летучие фенолы максимальные, мг/л |
0.015 |
0.015 |
|||||||
|
Fe среднее, мг/л |
1.08 |
0.42 |
1.08 |
0.65 |
1.48 |
0.5 |
|||
|
Fe максимальное, мг/л |
2.76 |
2.76 |
1.692 |
4.76 |
7.48 |
7.48 |
0.5 |
||
|
Cu средняя, мг/л |
0.005 |
0.118 |
0.118 |
0.039 |
0.001 |
||||
|
Cu максимальная, мг/л |
0.01 |
0.188 |
0.03 |
0.19 |
0.001 |
||||
|
Ni средний, мг/л |
0.007 |
0.027 |
0.01 |
||||||
|
Ni максимальный, мг/л |
0.166 |
0.166 |
0.021 |
0.08 |
0.01 |
||||
|
NO3 средние, мг/л |
0.112 |
0.27 |
0.27 |
0.07 |
0.629 |
9 |
|||
|
NO3 максимальные, мг/л |
0.551 |
0.242 |
2.32 |
1.542 |
9 |
||||
|
NO2 средние, мг/л |
0.06 |
0.036 |
0.114 |
0.061 |
0.079 |
0.039 |
0.047 |
0.02 |
|
|
NO2 максимальные, мг/л |
0.185 |
0.116 |
0.18 |
0.229 |
2.15 |
0.02 |
|||
|
NH4 средние, мг/л |
0.02 |
0.492 |
0.042 |
1.491 |
1.758 |
1.72 |
0.39 |
||
|
NH4 максимальные, мг/л |
1.558 |
0.063 |
3.848 |
4.053 |
4.459 |
0.39 |
|||
|
O2 средний, мг/л |
8.55 |
7.2 |
9.535 |
11.533 |
1.8 |
8.746 |
8.2 |
4 |
|
|
O2 минимальный, мг/л |
4.1 |
3.3 |
6.819 |
9.742 |
0.44 |
5.491 |
2.651 |
4 |
|
|
P средний, мг/л |
0.11 |
0.216 |
|||||||
|
P максимальный, мг/л |
0.208 |
||||||||
|
Zn средний, мг/л |
0.065 |
0.5 |
0.5 |
0.01 |
|||||
|
Zn максимальный, мг/л |
0.132 |
0.01 |
|||||||
|
Cd средний, мг/л |
0.004 |
0.004 |
0.001 |
||||||
|
Cd максимальный, мг/л |
0.008 |
0.008 |
0.001 |
||||||
|
SO4 средние, мг/л |
16.504 |
100 |
|||||||
|
SO4 максимальные, мг/л |
61.424 |
100 |
|||||||
|
Cr средний, мг/л |
0.01 |
0.004 |
0.005 |
0.02 |
|||||
|
Cr максимальный, мг/л |
0.068 |
0.015 |
0.023 |
0.02 |
|||||
|
Нефтепродукты средние, мг/л |
0.6 |
0.633 |
0.123 |
0.117 |
0.05 |
||||
|
Нефтепродукты максимальные, мг/л |
1.28 |
1.317 |
0.243 |
0.357 |
0.05 |
||||
|
СПАВ средние, мг/л |
1.2 |
0.038 |
0.064 |
0.1 |
|||||
|
СПАВ максимальные, мг/л |
2.5 |
0.119 |
2.5 |
0.1 |
|||||
|
H2 S средний, мг/л |
0.054 |
0 |
|||||||
|
H2 S максимальный, мг/л |
0.061 |
0 |
|||||||
|
Взвешенные вещества средние, мг/л |
46.6 |
368 |
368 |
||||||
|
Взвешенные вещества максимальные, мг/л |
160 |
1806 |
1806 |
||||||
|
Лигнин средний, мг/л |
0.2 |
||||||||
|
Лигнин максимальный, мг/л |
0.716 |
0.716 |
|||||||
|
Линдан максимальный, мг/л |
0.16 |
0.16 |
|||||||
|
Лигносульфонат средний, мг/л |
0.616 |
0.616 |
|||||||
|
Лигносульфонат максимальный, мг/л |
2.147 |
2.147 |
|||||||
|
Цианиды средние, мг/л |
0.325 |
0.325 |
0.05 |
||||||
|
Цианиды максимальные, мг/л |
2.29 |
2.29 |
0.05 |
||||||
|
Роданиды средние, мг/л |
0.283 |
0.283 |
0.1 |
||||||
|
Роданиды максимальные, мг/л |
0.604 |
0.604 |
0.1 |
||||||
|
Альфа-ГХЦГ средний, мг/л |
0.032 |
0.032 |
0.002 |
0.002 |
0.02 |
||||
|
Альфа-ГХЦГ максимальный, мг/л |
0.084 |
0.084 |
0.004 |
0.004 |
0.02 |
||||
|
Гамма-ГХЦГ средний, мг/л |
0.041 |
0.041 |
0.002 |
0.002 |
0.02 |
||||
|
Гамма-ГХЦГ максимальный, мг/л |
0.083 |
0.083 |
0.004 |
0.004 |
0.02 |
||||
|
Гексахлоран средний, мг/л |
0.006 |
0.006 |
0 |
||||||
|
Гексахлоран максимальный, мг/л |
0.027 |
0.027 |
0 |
||||||
|
Пропанид средний, мг/л |
0.003 |
0.003 |
0.0003 |
||||||
|
Пропанид максимальный, мг/л |
0.014 |
0.014 |
0.0003 |
||||||
|
ДДЭ среднее, мкг/л |
0.01 |
0.01 |
|||||||
|
ДДЭ максимальное, мкг/л |
0.04 |
0.04 |
|||||||
|
ДДД среднее, мкг/л |
0.04 |
0.04 |
|||||||
|
ДДД максимальное, мкг/л |
0.3 |
0.3 |
|||||||
|
Фториды средние, мг/л |
0.346 |
0.401 |
|||||||
|
Фториды максимальные, мг/л |
2.08 |
2.19 |
|||||||
|
Сатурн средний, мг/л |
0.05 |
0.05 |
0.0002 |
Таблица 21.
Экологически допустимые уровни факторов среды в р. Суре и Сурском водохранилище (в.у. — верхний уровень; н.у. — нижний уровень)|
Вид, возраст- |
ЭДУ |
||||||||||||
|
ная стадия |
БПК 5, мг/л (в.у.) |
Fe, мг/л (в.у.) |
O2 , мг/л (н.у.) |
Mn, мг/л (в.у.) |
NH4 , мг/л(н.у.; в.у.) |
NO2 , мг/л(н.у.; в.у.) |
NO3 , мг/л(н.у.; в.у.) |
Углеводороды, мг/л (в.у.) |
pH (н.у.; в.у.) |
Фенолы, мг/л (в.у.) |
PO4 , мг/л(н.у.; в.у.) |
Температура, 0C(н.у.; в.у.) |
Взвешенные вещества, мг/л (в.у.) |
|
Bosmina coregoni |
2.6 |
0.72 |
8 |
0.09 |
0.2; 0.555 |
0.034; 0.08 |
0.02; 0.52 |
0.034 |
8.07; 9.5 |
0.0058 |
0; 0.24 |
21; 27 |
11.5 |
|
Bosmina longirostris |
3.9 |
0.48 |
8.4 |
0.07 |
0.2; 0.76 |
0.046; 0.36 |
0.02; 0.68 |
0.52 |
7.93; 9.56 |
0.004 |
0.15; 1.14 |
19; 30 |
20.5 |
|
Chydorus sphaericus |
5.04 |
0.8 |
6 |
0.06 |
0.13; 0.65 |
0.035; 0.13 |
0.02; 0.49 |
0.122 |
8; 9.2 |
0.003 |
0; 0.12 |
22; 27 |
22.5 |
|
Daphnia cucullata |
2.6 |
0.64 |
8.4 |
0.04 |
0.2; 0.555 |
0.036; 0.08 |
0.07; 0.68 |
0.35 |
8.05; 9.45 |
0.0071 |
0.19; 1.14 |
21; 27 |
11 |
|
Daphnia longispina |
4.56 |
0.84 |
7.7 |
0.06 |
0.2; 0.75 |
0.042; 0.124 |
0.3; 0.87 |
0.034 |
8.12; 9.5 |
0.009 |
0; 0.095 |
20; 25 |
12 |
|
Eudiaptomus sp. |
12.16 |
0.84 |
8.4 |
0.09 |
0.2; 0.66 |
0.042; 0.124 |
0.36; 0.97 |
0.036 |
8.2; 9.45 |
0.0071 |
0.06; 0.26 |
21; 25 |
11 |
|
Keratella quadrata |
7.04 |
0.43 |
7.7 |
0.05 |
0.2; 0.555 |
0.029; 0.08 |
0.02; 0.76 |
0.093 |
7.76; 9.45 |
0.004 |
0.06; 0.26 |
20; 26 |
6.5 |
|
Mesocyclops leuckarti |
4.32 |
1.32 |
8.56 |
0.06 |
0.4; 2.9 |
0.042; 0.13 |
0.16; 0.84 |
0.037 |
7.98; 9.45 |
0.016 |
0; 0.12 |
19; 25 |
14 |
|
Личинки диаптомусов |
2.56 |
0.84 |
8.4 |
0.04 |
0.2; 0.555 |
0.042; 0.196 |
0.27; 0.97 |
0.037 |
8.07; 9.45 |
0.009 |
0.06; 0.26 |
19; 25 |
5.8 |
|
Личинки копепод |
4.8 |
0.87 |
8.08 |
0.07 |
0.6; 2.4 |
0.035; 0.16 |
0.02; 1.03 |
0.52 |
7.7; 9.56 |
0.0071 |
0; 0.22 |
20; 30 |
19 |
|
Науплии копепод |
3.9 |
0.69 |
8.16 |
0.06 |
0.2; 0.93 |
0.044; 0.36 |
0.02; 0.68 |
0.066 |
7.76; 9.56 |
0.016 |
0.06; 0.26 |
19; 26 |
16.5 |
|
Epistylis sp. |
3.2 |
1.21 |
4.9 |
0.14 |
0.508; 0.97 |
0.025; 0.057 |
0.52; 1.04 |
0.053 |
8.07; 9.5 |
0.009 |
0.14; 0.6 |
20.5; 23 |
9.6 |
|
Euchlanis dilatata |
7.44 |
1.5 |
4.8 |
0.42 |
0.83; 2.2 |
0.05; 0.89 |
0.12; 0.65 |
0.69 |
6.5; 7.8 |
0.0028 |
0.21; 2.4 |
20; 30 |
26 |
|
Eudiaptomus gracilis |
1.92 |
0.34 |
7.7 |
0.05 |
0.24; 0.84 |
0; 0.064 |
0.76; 6.5 |
0.053 |
7.5; 8.36 |
0.0037 |
0; 0.1.94 |
0; 20.5 |
5 |
|
ПДК |
3 |
0.3 |
4 |
0.1 |
0.5 |
3.3 |
45 |
6.5-8.5 |
0.001 |
0.25 |
|||
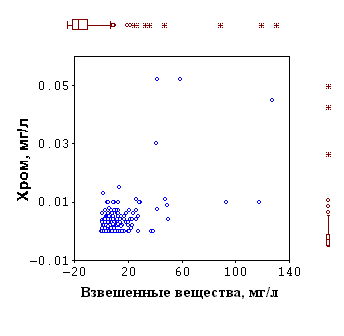
Рис. 1
. Диаграмма рассеяния для концентраций взвешенных веществ и хрома (справа "ящики с усами" для хрома, сверху — для взвешенных веществ)
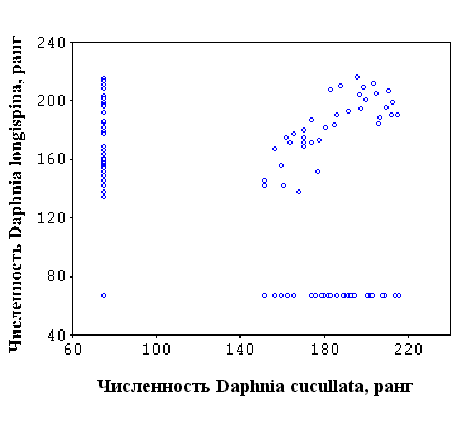
Рис. 2
. Диаграмма рассеяния для рангов численности D. cucullata и D. longispina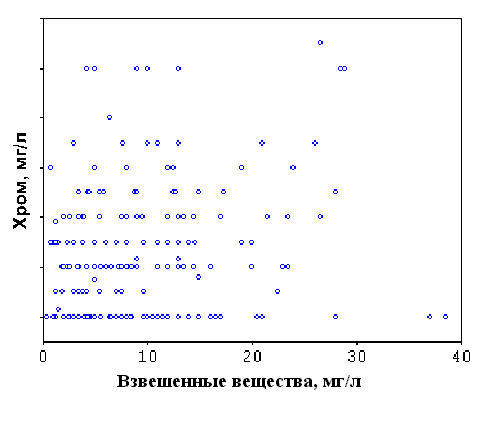
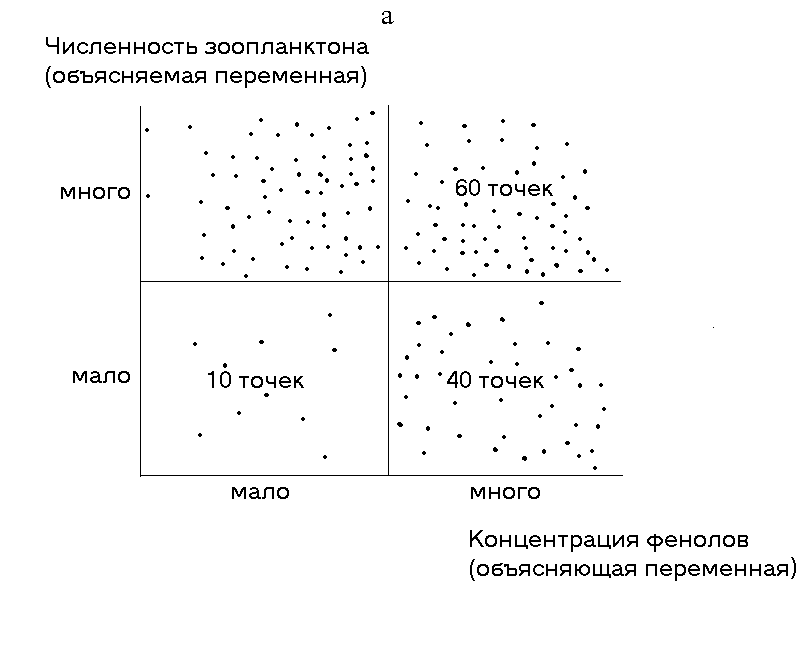
Рис. 4. Примеры вычисления точности и полноты при анализе правил ДА: а - точность и полнота меньше 100%; б - точность 100%; в - полнота 100%
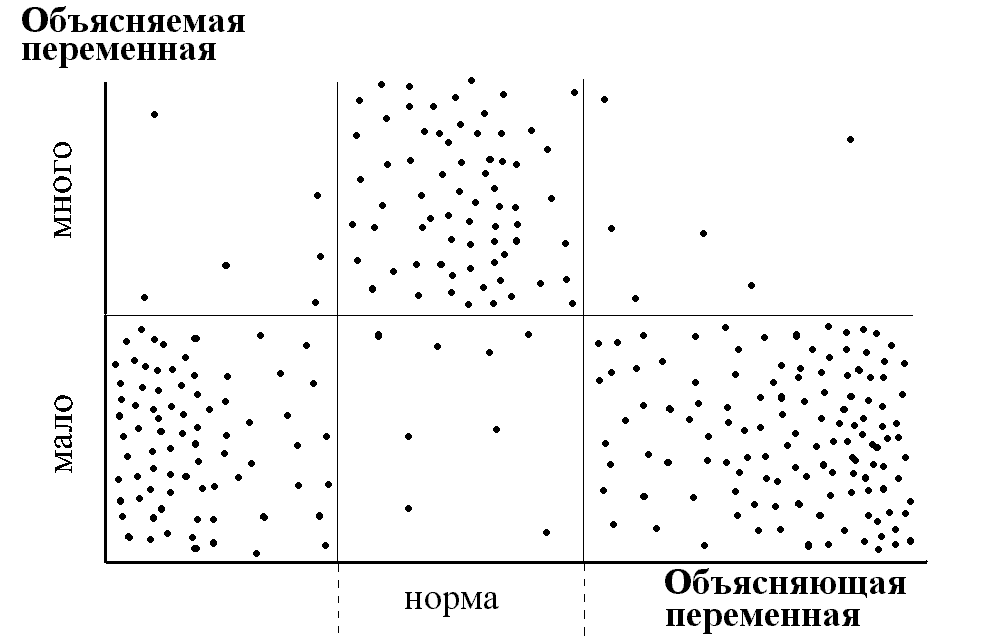
Рисунок 5. Оптимизация числовой переменной при установлении двусторонней границы

Рис. 6. Задание параметров функции желательности для переменной БПК5 по левой и правой границам оптимального диапазона. X — абсцисса текущего значения переменной, f(x) — доля измерений рассматриваемого признака, не превосходящих X, N(x) — количество измерений из общего числа, не превосходящих X, Xлев — задаваемая левая граница оптимального диапазона X
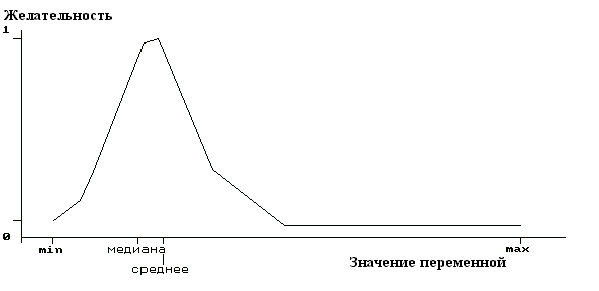
Рис. 7.
Функция желательности переменной БПК5, построенная по информации о левой и правой границах оптимального диапазона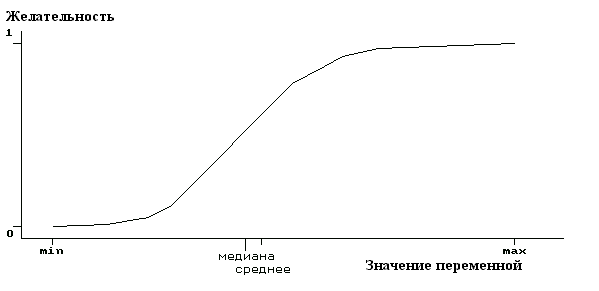
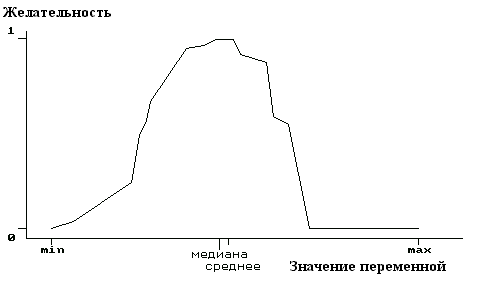
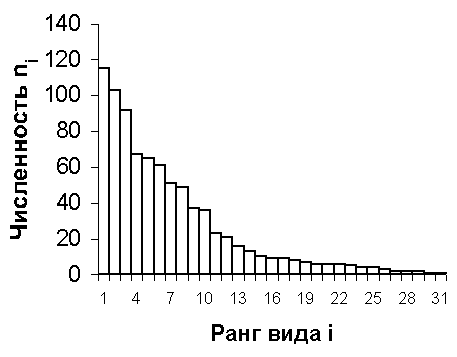
Рисунок 10.
Ранговое распределение обилия видов птиц в сыром жестколистном лесу Австралии (Driscoll, 1977; цит. по Мэгарран, 1992)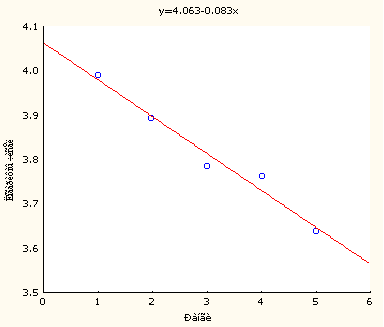
Рисунок 11.
Ранжировка случайных чисел по убыванию (полулогарифмический масштаб)
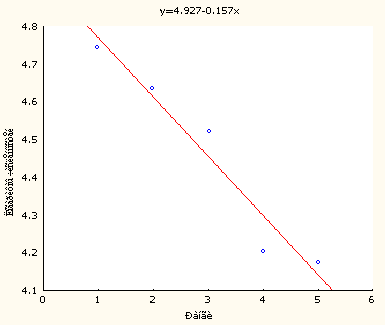
Рисунок 12.
Ранжировка видов птиц по убыванию численности (полулогарифмический масштаб)
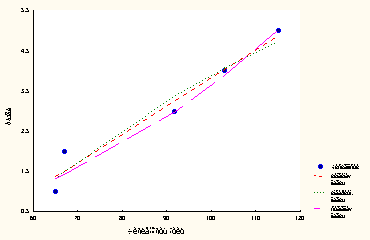
Рисунок 13.
Ранжировка видов по возрастанию численности (обычный масштаб). 1 — численности, 2 — линейная модель, 3 — логарифмическая модель, 4 — степенная модель
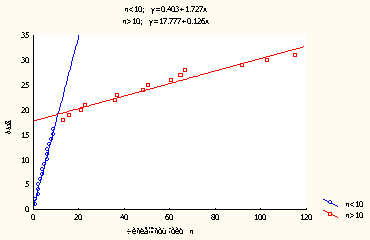
Рисунок 14.
Кусочно-линейная аппроксимация распределения птиц по возрастанию численности. 1 — численность не более 10 особей, 2 — численность больше 10 особей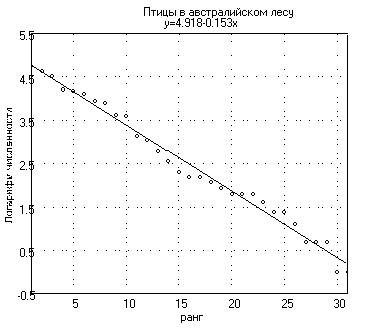
Рисунок 15.
Традиционное представление рангового распределения в полулогарифмическом масштабе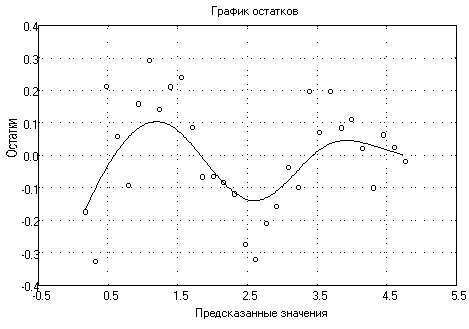
Рисунок 16.
График остатков для линейной модели на рис. 15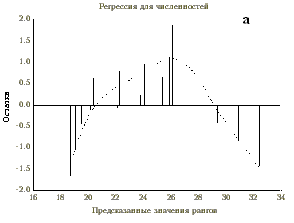

Рисунок 17.
Графики остатков для регрессии рангов относительной: а) численности 15 наиболее обильных видов; б) логарифмов численности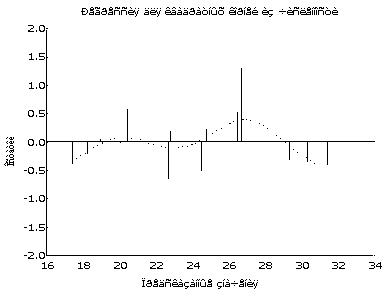
Рисунок 18.
Графики остатков для регрессии рангов относительно квадратных корней из численности 15 наиболее обильных видов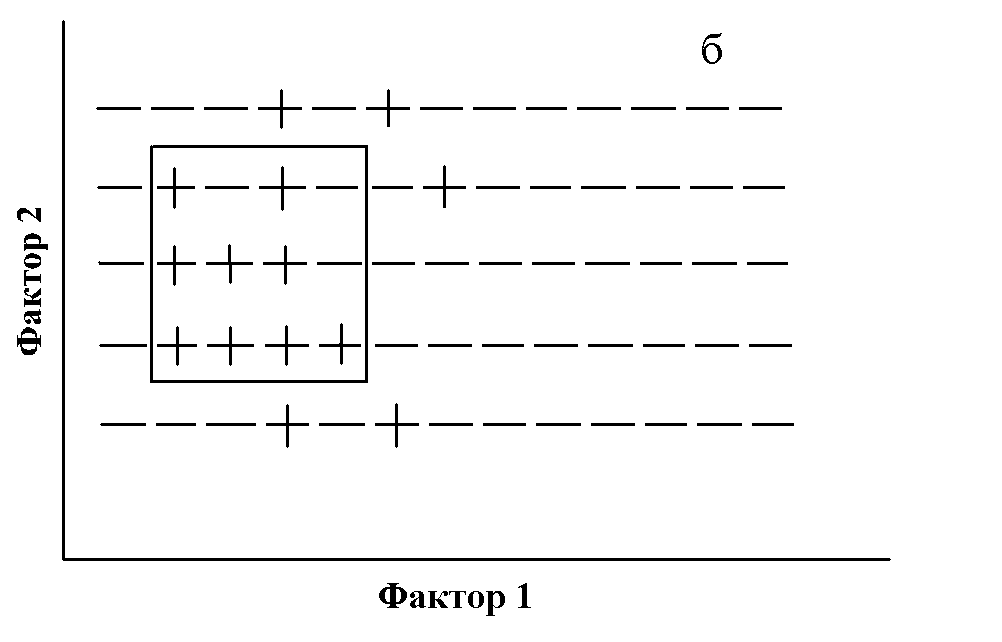
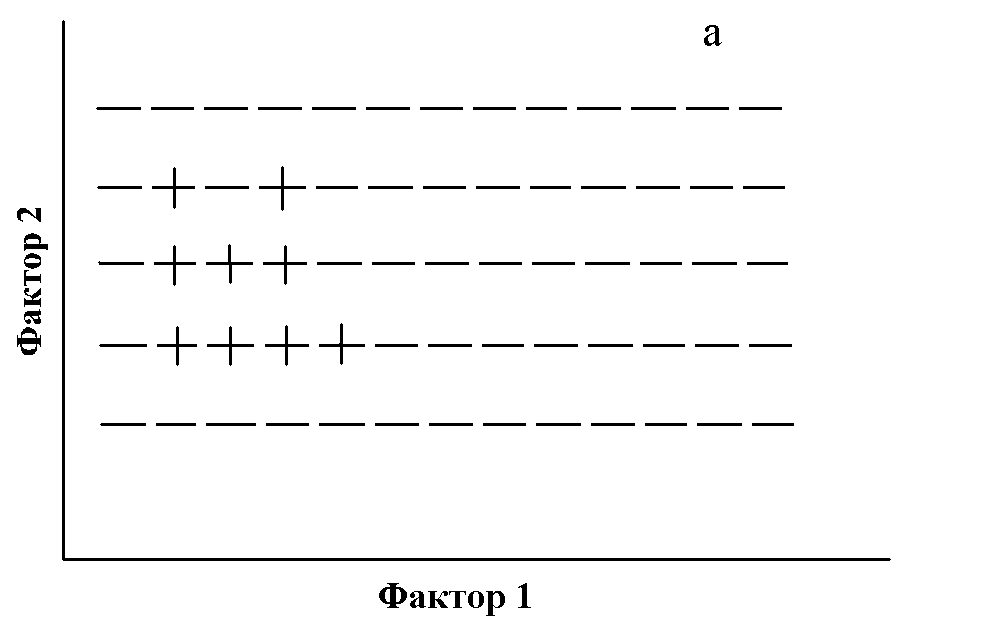
Рисунок 19.
Область нормального функционирования (знаки “плюс”) в окружении области аномального функционирования (знаки "минус") в пространстве факторов среды. а — идеальный случай, б — случай, приближенный к реальности
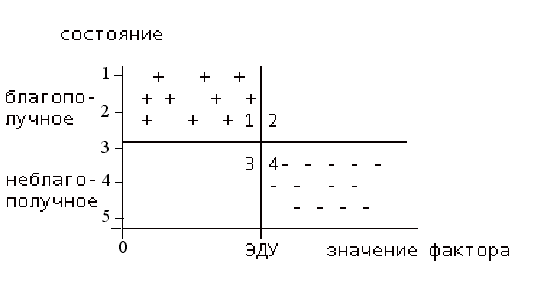
Рисунок 20.
Идеальная диаграмма распределения наблюдений для одномерного пространства факторов. Знаки "плюс" — благополучное состояние биоты, знаки "минус" — неблагополучное состояние биоты. Сектор 1 — благополучные наблюдения при соблюдении ЭДУ; сектор 2 — благополучные наблюдения при несоблюдении ЭДУ; 3 — неблагополучные наблюдения при соблюдении ЭДУ; 4 — неблагополучные наблюдения при несоблюдении ЭДУ
Рисунок 21.
Реальная диаграмма распределения наблюдений за экологическим состоянием фитопланктона для одномерного пространства факторов (концентрация ионов аммония). Цифры указывают число наблюдений с координатами, соответствующими данной точке координатной плоскости; знак # означает, что число наблюдений было более 9. На уменьшенной диаграмме слева внизу цифры обозначают количество наблюдений в каждом квадранте; на такой же диаграмме справа внизу указано процентное соотношение наблюдений в каждом квадранте.Рисунок. 22.
График зависимости полноты от точности при оптимизации числовой переменной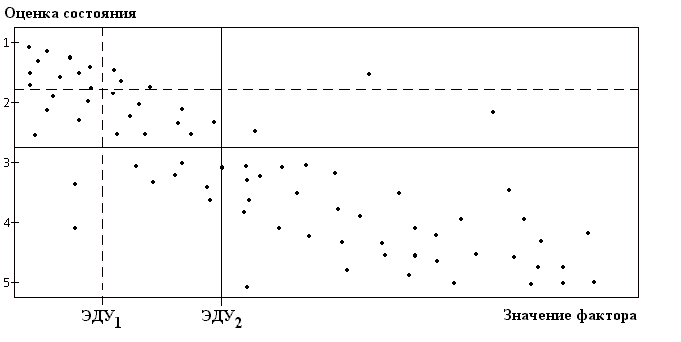
Рисунок 23.
Границы между благополучием и неблагополучием состояния биоты и значения ЭДУ в различных природных экосистемах. Сплошные линии — техногенная территория, пунктир — зона рекреации.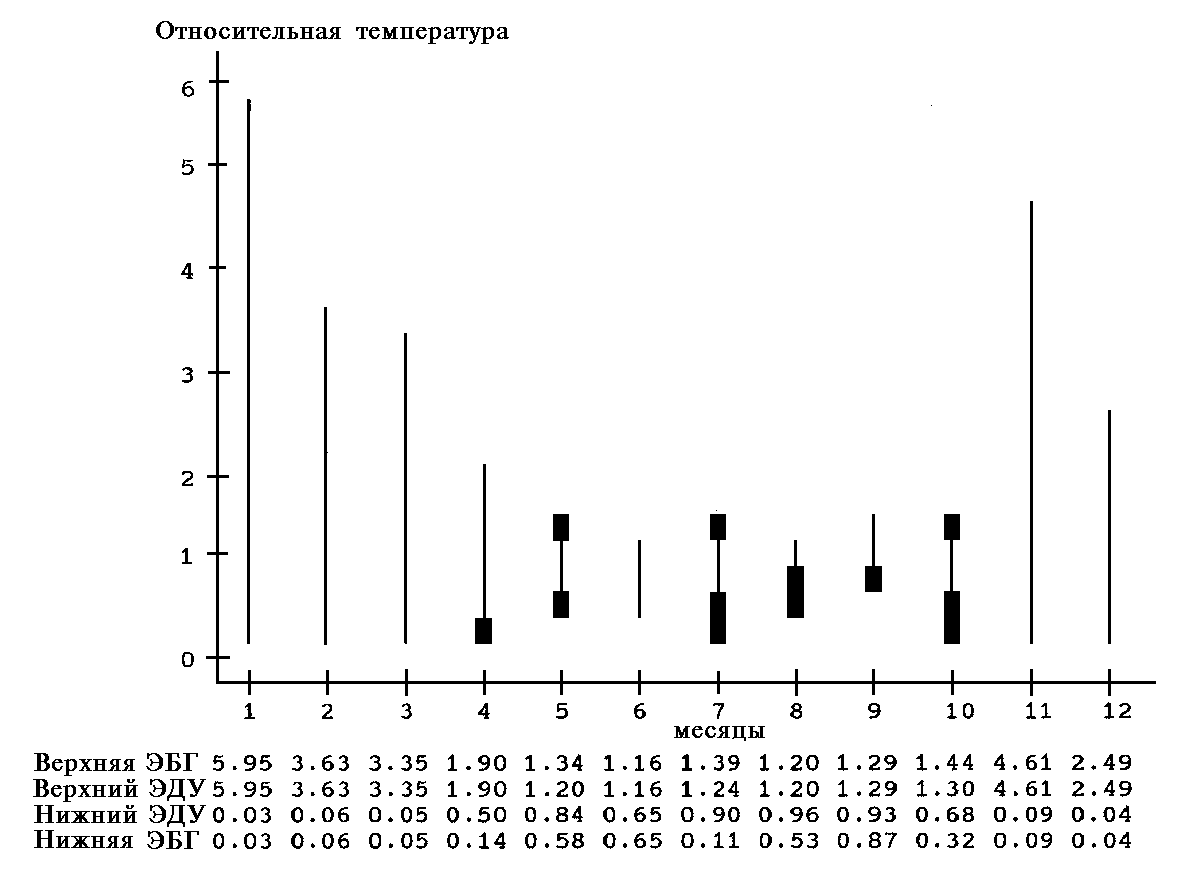
Рисунок 24.
Динамика экологически допустимых уровней (ЭДУ) и экологически безопасных границ (ЭБГ) переменной "Относительная температура" для оценки состояния планктона и перифитона. Тонкие линии обозначают интервалы значений переменной, в пределах которых оценка урожайности благополучна. Утолщенные столбики показывают интервал значений от ЭДУ до ЭБГ, в пределах которого урожайность падает ниже границы благополучия. Отсутствие столбика означает, что данный фактор является незначимым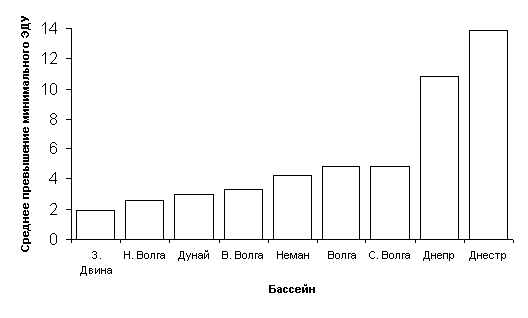
Рисунок 25.
Ранжирование речных бассейнов европейской части бывшего СССР по средней величине относительного ЭДУ физико-химических факторов
Рисунок 26.
Усредненные значения относительных экологически допустимых уровней (ОЭДУ) физико-химических факторов: 1 — водная толща, 2 — грунты.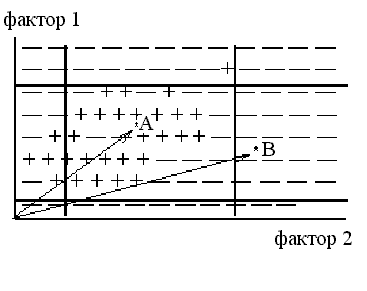
Рисунок 27.
Прогноз экологического состояния на основе выделенной области нормального функционирования биоты. Сценарий A — благополучный прогноз, сценарий B — неблагополучный прогноз. Знаки "плюс" и "минус" — состояние биоты соответственно благополучно и неблагополучно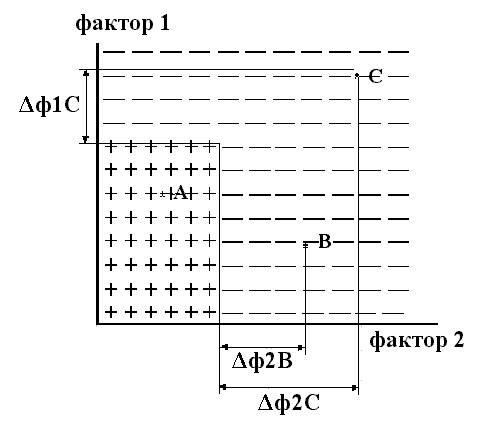
Рисунок 28.
Управление качеством среды с целью возвращения в область нормального функционирования биоты. D ф2B — величина, на которую надо уменьшить значение фактора 2, чтобы вернуть состояние биоты из точки B в область нормального функционирования; D ф1C и D ф2C — величины, на которые надо уменьшить соответственно значения факторов 1 и 2, чтобы вернуть состояние биоты из точки C в область нормального функционирования