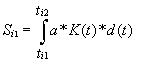 и
и 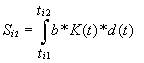 ,
, и специфика физического и биологического времени
как фундаментального свойства времени.
Начиная с Аристотеля, во все последующие времена одним из наиболее важных и фундаментальных свойств времени считалась и по сей день считается равномерность. Однако вплоть до возникновения классической механики не было сколь-либо серьезных попыток обосновать подобное представление. Даже в те далекие времена, когда еще не было механических часов, позволяющих практически измерять интервалы равномерного времени и неограниченно долго вести счет равных друг другу единиц измерения времени, и когда в повседневной практике вынуждены были пользоваться постоянно изменяющимися в течение года, и в общем случае не равными друг другу "дневными" и "ночными" часами (в силу чего далеко не самоочевидным было утверждение Гераклита о том, что “один день равен всякому”), даже в этих условиях мыслители проявляли удивительную уверенность в том, что истинное время на самом деле течет равномерно.
Аристотель, как мы видели, рассматривал равномерность в качестве одного из наиболее фундаментальных свойств времени. Равномерность, наряду с общедоступностью и максимальной простотой, является у Аристотеля важнейшим критерием при поисках движения, наиболее пригодного для измерения времени. Таким движением Аристотель считает суточное вращение небесной сферы, или "сферы неподвижных звезд".
С его точки зрения, равномерность - настолько общеизвестное и самоочевидное свойство времени, что указание на него является веским аргументом при доказательстве истинности тезиса: "время не есть движение". “Изменение и движение каждого [тела], - пишет Философ, - происходит только в нем самом или там, где случится быть самому движущемуся и изменяющемуся; время же равномерно везде и при всем. Далее, изменение может идти быстрее и медленнее, время же не может, так как медленное и быстрое определяется временем: быстрое есть далеко продвигающееся в течение малого времени, медленное же - мало [продвигающееся] в течение большого [времени]; время же не определяется временем ни в отношении количества, ни качества” /Физ,IV,10,218b10-15/.
Согласно данному утверждению, для определения большего и меньшего движения мы должны иметь возможность сравнивать, какое расстояние проходят движущиеся тела за равные или заведомо большие или меньшие по сравнению с данным отрезком времени интервалы, т.е. здесь предполагается, что мы априори умеем оценивать и сравнивать между собой различные интервалы времени. Это возможно только в том случае, если мы допускаем, что время всегда течет одинаково, т.е. равномерно, и что наши единицы измерения времени (например, полные сутки) каждый раз одинаковы по длительности.
Некоторым обоснованием равномерности выглядит следующее суждение Аристотеля: "...Время не называется быстрым и медленным, а большим и малым, долгим и коротким. Поскольку оно непрерывно, оно долгое и короткое, поскольку оно число - большое и малое, а быстрым и медленным не бывает; ведь ни одно из чисел, служащих для счета, не может быть быстрым и медленным" /Физ., IV,12, 220b1-5/.
Однако здесь лишь утверждается, что быстрота и медленность представляют собой количественные показатели движения, отнесенные к единице времени. Количественные же выражения самого времени не могут быть отнесены к каким-то иным единицам времени и поэтому представляют собой просто числа, которые нельзя характеризовать как быстрые или медленные.
Единственное, на чем основывается представление о равномерности времени, - это интуитивная уверенность Аристотеля в том, что время - это нечто априори равномерное. И это не случайно. Дело в том, что, во-первых, невозможно непосредственно сравнивать между собой, как бы накладывая друг на друга, длительности таких естественных единиц измерения времени, как, например, длительности полных суток; во-вторых, во времена Аристотеля не существовало таких измерителей времени, как механические часы, которые достаточно долго сохраняли бы постоянство своего хода и таким образом давали бы возможность измерять и сравнивать между собой длительности отстоящих друг от друга интервалов времени.
Но проблема равномерности времени, как мы увидим позднее, не снимается даже после появления механических часов, поскольку для определения постоянства или непостоянства их хода необходимо или непосредственно сравнивать между собой следующие друг за другом отмериваемые ими единицы времени, что в принципе невозможно; или иметь некоторый заведомо равномерный стандарт измерения времени, но тогда проблема равномерности в полной мере переносится на этот стандарт; или, наконец, придумать какие-то особые критерии равномерности. Поэтому было бы тщетно искать у Аристотеля какое-либо обоснование равномерности времени, и, что бы ни думал сам Философ, единственным основанием представления о равномерности как о фундаментальном свойстве времени остается его (Аристотеля) интуитивная уверенность в том, что "время... равномерно везде и при всем".
Не преуспели в обосн††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††сненного как бы путем размышления" /Эннеады,III,7,1; Браш,с.458//4/. Так же, как и Аристотель, он считает равномерность самоочевидным свойством движений, при помощи которых можно измерять время, если мы придерживаемся концепции, согласно которой время есть мера движения /III,7,9/. Поясняя точку зрения Платона на роль небесных светил, которые возникли для того, чтобы указывать время, установить в нем известные границы и служить ясным до очевидности масштабом его измерения, Плотин пишет: "Только таким образом мы, рассматривая время от одного восхода солнца до другого, могли выработать понятие об определенной продолжительности равномерного движения, положенного нами в основу измерения" /III,7,12;Браш, с.469/. И хотя Плотин, следуя за Платоном, здесь вполне правильно указывает на полные сутки как на равные друг другу интервалы времени, тем не менее в основе его уверенности в том, что полные сутки по длительности равны друг другу, не могло лежать ничего, кроме интуиции.
Равномерность времени обретает у Плотина своеобразный, скорее, качественный, чем количественный, смысл. Так, охарактеризовав время как "жизнь души", причем "жизнь, соответствующую определенной силе умопостигаемой души" /III 7,11;Браш, с.468/, Плотин пишет, что время "является измерением длины подобной жизни; эта длина развертывается в бесшумно наступающих изменениях, которые протекают равномерно" /III 7,12; Браш, с.469/.
Астрономы и философы-номиналисты позднего средневековья, как мы видели, продолжают рассматривать равномерность как одно из основных и самоочевидных свойств истинного времени. При определении движения, пригодного для измерения времени "в наиболее собственном смысле", средневековые последователи Аристотеля ради равномерности даже жертвуют таким его требованием к "мировым часам", как общедоступность для наблюдения ("наибольшая известность"), и признают в качестве такого движения вращение невидимой гипотетической "девятой" сферы. В результате происходит отделение равномерного времени от всех чувственно воспринимаемых движений и таким образом формируется идея абстрактного "математического времени", которое, в отличие от "времен", измеряемых при помощи чувственно воспринимаемых движений, протекает равномерно.
Однако средневековые перипатетики, хотя и оказались вынужденными обсуждать вопрос о множественности времен, тем не менее так же, как и Аристотель, не раскрыли природу равномерности "времени в наиболее собственном смысле" (т.е. времени "первого движения") и не смогли обосновать правомерность использования равномерного времени, отсчитываемого при помощи невидимой "девятой сферы", для измерения неравномерных земных движений. Как пишет В.П. Зубов, “позднейшее объяснение арабских мыслителей (Аверроэса), вводившее новое произвольное допущение космологического порядка, а именно указание на причинную обусловленность всех "подлунных движений" движением "мировой сферы", также не было ответом на поставленный вопрос. Единственное, что, быть может, заслуживает внимания, это более четкое различение двух видов мер: время обращения мировой сферы есть "внутренняя" мера движения этой самой сферы, для всех же других движений время ее обращения есть "внешняя", или непосредственно не связанная, с ними мера (mensura separata)” /Зубов, 1960, с.35/. Нерешенным, по мнению Зубова, остался также вопрос о том, что гарантирует равномерность вращения небесной сферы.
Природа и критерии равномерности времени оставались невыясненными и во времена И. Ньютона.
Так, Джон Локк (1632-1704) считал, что понятия последовательности и продолжительности мы получаем не из наблюдений внешнего движения, а из рефлексии последовательной цепи идей, появляющихся друг за другом в нашем уме /Локк, т. 1, 1985, с.232/. Согласно Локку, цепь идей в уме человека имеет известную степень быстроты. Этот тезис обосновывается тем, что человек не воспринимает как слишком быстрые, так и слишком медленные движения. В первом случае события, слишком быстро следующие друг за другом, занимают время одной идеи и не могут быть различимы людьми. В случае же слишком медленных движений, “...другие идеи наших собственных мыслей имеют... возможность проникать в наш ум между идеями, которые доставляет нашим чувствам движущееся тело...", и "чувство движения исчезает”/Там же, с. 235/ (Здесь и далее курсив автора. - И.Х.)..
Следующим после приобретения идеи продолжительности естественным делом ума является “приобретение некоторой меры для этой общей продолжительности, по которой он мог бы судить о ее различной величине и рассматривать определенный порядок, в котором существуют вещи... Такое рассмотрение продолжительности как ограниченной известными периодами и обозначенной определенными мерами, или эпохами..., и есть то, что мы называем собственно временем” /Там же, с.237-238/.
Итак, согласно Локку, время есть измеренная продолжительность. Причем хорошее измерение должно делить всю его продолжительность на равные периоды. Вместе с тем философ прекрасно понимает, что “мерой продолжительности может быть только продолжительность...” /Там же, с. 238/ и поэтому невозможно иметь “...какую-нибудь установленную неизменяемую меру продолжительности, состоящей в постоянной текучей последовательности, подобно тому, как мы имеем меры для измерения протяженных величин - дюймы, футы, ярды и т.д., раз отмеченные на прочном материале” /Там же/. Поэтому для измерения времени “может быть пригодно только то, что разделило всю величину его продолжительности на очевидно равные части постоянно повторяющимися периодами” /Там же/.
Такой наиболее подходящей мерой времени, считает Локк, являются вращения Солнца и Луны. Но в результате постоянного измерения времени при помощи этих движений люди стали думать, “будто движение и продолжительность измеряются одно другим, ибо при измерении величины времени люди привыкли к идеям минут, часов, дней, месяцев, лет и т.д. и о них начали думать всякий раз при упоминании о времени или продолжительности (а все эти отрезки времени измерялись движением небесных тел). Поэтому они стали склонны смешивать время и движение или по крайней мере думать, что они необходимо связаны друг с другом” /с.238/. На самом же деле, по Дж. Локку, время измеряется не самим движением Солнца, а его периодичностью, и поэтому для измерения времени не обязательно иметь какие-либо движения, а необходимо и достаточно иметь периодические процессы. “И если бы замерзание воды или цветение растения повторялись во всех частях света через равноотстоящие периоды, то они служили бы людям для счета лет так же хорошо, как и движение Солнца” /с.239/. Поэтому “мы... должны тщательно различать саму продолжительность от мер, которыми мы пользуемся для суждения о ее величине. Продолжительность сама по себе должна рассматриваться как движущаяся вперед одним постоянным, ровным и однообразным потоком. Но насколько нам дано знать, такою не способна быть ни одна из тех ее мер, которыми мы пользуемся; не можем мы быть уверены и в том, что их определенные части, или периоды, равны между собой по продолжительности, ибо, как бы мы ни измеряли две последовательные величины продолжительности, никогда нельзя доказать их равенства” /Там же, с. 240/.
В отличие от используемых в качестве меры времени периодических процессов, равенство периодов которых всегда остается под сомнением, понятие самой продолжительности, считает Локк, остается тем не менее ясным. Поскольку нет возможности непосредственно сопоставить длительности двух частей последовательности и поэтому нельзя знать с достоверностью их равенства, то для измерения времени остается только принять за меру времени непрерывные последовательные явления, следующие через периоды, кажущиеся равноотстоящими. Для определения этого равноотстояния “у нас нет другой меры, кроме той, которую для нашего убеждения в их равенстве в согласии с другими вероятными доводами запечатлела в нашей памяти цепь наших собственных идей” /с.241/. Иными словами, реально существует неограниченно длящаяся как в прошлое, так и в будущее равномерная продолжительность, ясную идею которой человек получает путем рефлексии равномерного потока идей в своем уме. Время же есть ограниченная часть этой продолжительности, измеренная той или иной относительно точной мерой - часом, сутками, годом и т.д.
Таким образом, согласно Локку, представление человека о равномерной длительности возникает в результате существования у него некоторой "постоянной и правильной последовательности идей", т.е. некоторого внутреннего движения идей или, выражаясь современным языком, "потока сознания". Однако кроме общих заверений, что это так и только так, Дж. Локк не может привести каких-либо разъяснений, почему "цепь наших собственных идей" всегда следует с одной и той же неизменной скоростью.
Итак, в доньютоновской истории философии и естествознания равномерность хотя и рассматривается мыслителями как важнейшее свойство времени, тем не менее не подвергается глубокому критическому анализу, а принимается как "естественное", самоочевидное свойство времени. Единственным основанием представления о равномерности времени (или длительности) оставалось субъективное чувство времени или интуиция равномерного дления.
Безотносительная к каким бы то ни было чувственно воспринимаемым процессам равномерность используемого в астрономии “математического времени” приобретает особое значение в классической физике. Однако И. Ньютон (1643-1727), вводя понятия “абсолютного” и “относительного” времени, по сути дела постулирует равномерность абсолютного времени, считая это свойство времени общеизвестным, и ограничивается лишь указанием на то, что в астрономии абсолютное время отличается от обыденного солнечного времени так называемым уравнением времени. Следовательно, согласно И. Ньютону, достаточным (по крайней мере, для астрономических целей) приближением к абсолютному времени является обыденное солнечное время, выправленное при помощи уравнения времени. Неравномерность же обыденного солнечного времени, как известно, проистекает в основном из-за наложения на вращение Земли вокруг оси других ее движений. Уравнение времени, о котором пишет И. Ньютон, позволяет, по сути дела, выделить в “чистом виде” вращение Земли вокруг оси и пользоваться им как эталонным равномерным движением для измерения “более правильного”, или, точнее, более равномерного времени.
Более подробно, чем И. Ньютон, проблему измерения времени обсуждает Жан Лерон д΄Аламбер (1717-1783).
Ж.Л. д’Аламбер считал, что все доступные познанию свойства движения, пространства, времени и материи постигаются математикой или такими науками, как механика и физика, которые опираются в своей методологии на математику. Вопросы же о сущности познаваемых объектов д’Аламбер отвергает как "метафизические". Этими вопросами, считает он, могут заниматься лишь философские сектанты, которые, несмотря на все различия их сект, при познании, например, пространства, вынуждены пользоваться одной и той же геометрией.
Вполне понятно, что, стоя на подобных позициях, д’Аламбер не мог без критического анализа и определенной конкретизации признать в качестве объекта познания такую априорно постулируемую И. Ньютоном сущность, как "абсолютное, истинное математическое время". Принимая и отстаивая ньютоновскую концепцию времени, д’Аламбер не может, конечно, сделать абсолютное время доступным непосредственному восприятию и познанию. Более того, он согласен с Ньютоном в том, что, возможно, и не существует такое абсолютно равномерное движение, при помощи которого можно было бы измерять абсолютное время. Вместе с тем он не может довольствоваться априорным постулированием равномерности времени и стремится доказать, что равномерность абсолютного времени - это его объективное свойство, которое вполне поддается выявлению и математической фиксации.
Следует признать, что д’Аламбер преуспел в решении этой проблемы, поскольку он обратил внимание на одно весьма важное свойство равномерных и только равномерных механических движений, заключающее в том, что отношение расстояний, пройденных двумя равномерно движущимися телами за один и тот же интервал времени, оказывается величиной постоянной для любых произвольно выбранных (не равных нулю) интервалов длительности, и предложил использовать это свойство в качестве критерия равномерности.
Но прежде чем рассмотреть предложенный д'Аламбером критерий равномерности, позволяющий выделить пригодные для измерения времени равномерные процессы, кратко остановимся на посленьютоновской эволюции идеи абсолютного времени классической физики. Это позволит нам более адекватно оценить даламберовский критерий равномерности и раскрыть его истинное значение в развитии представлений о времени.
Сформировавшаяся еще в конце средневековья и на протяжении трех столетий господствовавшая в сознании естествоиспытателей идея "математического времени" как некоторой абстрактной абсолютно равномерной независимой переменной, используемой при расчетах движений небесных тел, в ньютоновской механике обретает субстанциальность и превращается в некую реально существующую и равномерно текущую сущность. Но вместе с тем, хотя между "математическим временем" доньютоновской астрономии и механики и абсолютным временем ньютоновских "Начал" и существует определенная генетическая связь, тем не менее усвоение идеи абсолютного времени, равно как и самих "Начал", несомненно, потребовало от исследователей определенных усилий и достаточно длительного времени. Формальное сходство "математического времени" доньютоновской астрономии и механики с абсолютным временем ньютоновских "Начал" создают иллюзию легкости и беспроблемности для естествоиспытателей XVII- XVIII вв. усвоения ньютоновских представлений о времени. Только в работах тех великих последователей И. Ньютона, которые проявили себя не только как естествоиспытатели, но и как философы, задумывавшиеся о содержании и сущности исходных понятий естествознания, можно уловить коллизии протекавшего на протяжении, по крайней мере, первой половины XVIII века процесса утверждения ньютоновской концепции времени.
Как мы показали в первой главе, характерный для естествознания феноменологический подход к времени лишь как к количественной мере движения в сущностном, онтологическом плане дополнялся различного рода философскими и теологическими концепциями, характерной особенностью которых была тенденция субъективации времени. Поэтому естествоиспытатели, которые не только восприняли ньютоновскую концепцию времени, но и стремились ее обосновать и утвердить, были вынуждены обратить особое внимание на проблему объективности времени.
Так, Леонард Эйлер (1707-1783) в "Механике" (1736) и в "Теории движения твердых тел" (1765) отстаивает идею абсолютно равномерного временного течения и, не называя имен, полемизирует с теми, кто субъективирует время. У Л. Эйлера сохраняются и некоторые элементы традиционных представлений о времени. В частности, он считает, что человек обладает внутренним, безотносительным к наблюдаемым движениям чувством времени и способностью интуитивно определять равенство различных интервалов длительности. Он пишет, что “если бы у нас, как некоторые склонны думать, не было других средств для определения времени, кроме как из рассмотрения движения, то мы не могли бы признать ни времени без движения, ни движения без времени...” /Эйлер, 1938, с. 278/. Правда, Эйлер отмечает, что делить время мы научились от наблюдений за движением Солнца, но “и без помощи движения мы имеем представление о том, что такое до и после, а отсюда, по-видимому, само собой вытекает понятие последовательности” /Там же/. И хотя более детальным познанием времени мы обязаны рассмотрению движения, “отсюда еще не следует, что время само по себе представляет собой не что иное, как лишь то, что мы воспринимаем. Что представляют собой два равных промежутка времени, это понимает всякий, хотя бы в течение этих промежутков, может быть, и не произошло равных изменений, на основании которых можно было бы прийти к заключению о равенстве этих промежутков времени” /с. 279/.
Вместе с тем Эйлер считает, что “деление времени на части не является чисто умственной операцией, как обыкновенно утверждают те, которые помещают время только в нашем сознании, не отделяя понятия времени от самого времени.
В самом деле, если бы время представляло собой не что иное, как последовательность наступающих друг за другом явлений, и если бы вне нашего сознания не существовало никаких средств для измерения времени, то нам ничто не мешало бы при всяком движении считать равными те части времени, в течение которых проходятся равные пути, так как они кажутся следующими друг за другом через равные промежутки. Следовательно, мы могли бы с одинаковым основанием рассматривать любое движение как равномерное. Однако сама природа вещей достаточно убедительно свидетельствует, что равномерное движение существенно отличается от неравномерного; следовательно, равенство промежутков времени, на котором это основывается, представляет собой нечто большее, чем содержание наших понятий” /с. 284-285/.
Здесь мы наблюдаем, фактически, стремление сочетать представление о времени как о некоторой абстракции от наблюдаемых движений с ньютоновской идеей абсолютного времени.
Развернувшаяся в конце XIX - начале XX вв. критика идеи абсолютного времени классической физики раскрыла несостоятельность представлений о времени как о некоторой самостоятельной равномерно текущей сущности. Однако в период становления и поступательного развития ньютоновской механики даже основоположники позитивизма О. Конт (1798-1857) и Г. Спенсер (1820-1903) не смогли разглядеть в ньютоновских абсолютных пространстве и времени ненавистных им априорных метафизических сущностей. И хотя основоположники позитивизма чувствуют и понимают всю сложность интерпретации понятий пространства и времени, тем не менее им кажется, что за априорными метафизическими идеями абсолютных пространства и времени классической физики скрывается некая реальность.
Так, например, Г. Спенсер считает, что наше сознание непосредственно свидетельствует о том, что “пространство и время существуют не в мысли, а вне ее и столь абсолютно не зависят от нее, что их нельзя понять, как переставшими существовать даже в том случае, если ум перестал существовать” /Спенсер, т.1, с. 28/. Правда, пространство и время как таковые не могут быть познаны ни как сущности, ни как атрибуты сущностей. Они познаются лишь в отношении к сознанию. Время - это абстракт отношения последовательности, а пространство - абстракт отношения сосуществования /с. 93/. При этом понятия пространства и времени, как и другие абстрактные понятия, образуются из отдельных конкретных фактов, но их отличие “состоит в том, что, в данном случае, систематизация опыта прошла через всю эволюцию мышления” /с. 93/.
Мы не ставим здесь целью проанализировать представления Г. Спенсера о времени. Для нас важно подчеркнуть, что Г. Спенсер полагает, что хотя мы познаем лишь относительную реальность, тем не менее постоянство нашего сознания о времени свидетельствует о существовании некоторой абсолютной реальности. И хотя мы не можем познать причины, обусловливающие отношение последовательности, и обладаем лишь относительным знанием, тем не менее должны без колебаний принять те термины мысли, которые образовались в нас в силу опыта. Таким образом, можно сказать, что Г. Спенсер принимает в целом ньютоновскую концепцию времени.
Что касается критики ньютоновских концепций пространства и времени со стороны Лейбница и Канта, то, как отмечает У.И. Франкфурт /Франкфурт, 1978, с. 157/, эта критика, не имея под собой достаточных оснований для физической дискуссии, осталась на чисто философском уровне и не оказала сколь-либо заметного влияния на сознание естествоиспытателей. В результате ньютоновская идея абсолютного времени вплоть до конца XIX столетия оказывается единственной научной концепцией и в сознании естествоиспытателей настолько естественной, самоочевидной, не требующей никакого обсуждения и обоснования, что становится возможным строить всю аналитическую механику, а в дальнейшем и все другие разделы физики без какого бы то ни было обсуждения свойств и сущности времени.
Ньютоновское представление о времени на протяжении более чем 200 лет оставалось незыблемым как среди естествоиспытателей, так и среди значительной части философов. Правда, в философии параллельно развивались и иные, в частности кантианские, взгляды на время, но до конца XIX столетия они не оказывали заметного влияния на развитие естествознания.
К концу XIX века “механика, идущая по своему победоносному пути в разрешении различных проблем по естествознанию, достигает своего апогея” /Жуковский, 1937, т. IX, с. 245/ и в своем стремлении всяческому физическому явлению давать механическое толкование останавливается перед объяснением некоторых накопленных в физике опытных данных. Возникает необходимость приложить начала классической механики “не к простейшим элементам механики - силе и массе, а к различным физическим элементам: магнитному полюсу, элементу тока, наэлектризованному шарику, электрону, квантам и т.д.” /Там же/. Трудности в объяснении накопленных в физике фактов наводят исследователей на мысль, что возможно они не могут быть объяснены с помощью начал классической механики и что для их объяснения нужны некоторые видоизменения этих начал /Там же/.
В этот период начинает осознаваться абстрактность понятий абсолютного пространства и времени; вновь становятся актуальными проблемы измерения времени, определения одновременности пространственно удаленных друг от друга событий и т.д. До естествоиспытателей доходит, наконец, и кантианская критика исходных ньютоновских понятий классической физики. Так, Г.Р. Герц (1857-1894) предпринимает попытку изложить механику, исходя из кантианских представлений о пространстве и времени (См: /Герц,
1959/).Критический анализ ньютоновских представлений о пространстве и времени одним из первых среди естествоиспытателей начал Эрнст Мах (1838-1916). Э. Мах отмечает, что равномерное движение - это такое движение, при котором одинаковые приращения пройденного телом пути соответствуют равным изменениям другого тела, служащего в качестве эталона (например, вращение Земли). “Вопрос, равномерно ли движение само по себе, не имеет никакого смысла. В такой же мере мы не можем говорить об "абсолютном времени" (независимо от всякого изменения). Это абсолютное время не может быть измерено никаким движением, и поэтому не имеет никакого ни практического, ни научного значения; никто не вправе сказать, что он что-нибудь о таком времени знает, это праздное "метафизическое" понятие” /Мах, 1909, с. 187/.
Идею абсолютного времени подверг критике Анри Пуанкаре (1854-1912). Он пишет, что у человека нет непосредственной интуиции равенства двух промежутков времени, и мы не можем быть уверены в равенстве длительности повторяющихся процессов..
При измерении времени такими движениями, как качания маятника, считает Пуанкаре, мы принимаем постулат, согласно которому “длительность двух идентичных явлений одна и та же; или, если угодно, что одни и те же причины требуют одного и того же времени, чтобы произвести одни и те же действия” /Пуанкаре, 1990, с.222/. Однако, пишет он далее, следует быть осторожными. “Не может ли случиться так, что в один прекрасный день опыт опровергнет наш постулат?” /Там же/. Подводя итоги обсуждению проблемы измерения времени, А. Пуанкаре делает вывод, что отсутствующую у нас интуицию равенства двух промежутков времени мы заменяем некоторыми правилами, которые мы выбираем “не потому, что они истинны, а потому, что они наиболее удобны...” /с. 232/.
Таким образом, в конце XIX столетия вопрос о равномерности времени вновь стал проблематичным.
Не раскрыл природу равномерности и Альберт Эйнштейн (1879-1955).
В специальной теории относительности (СТО) предполагается, что в каждой точке пространства локальное время течет равномерно, и это фиксируется расположенными в этих точках вполне идентичными часами. Для того чтобы синхронизировать часы, находящиеся в разных точках пространства, достаточно обменяться между этими точками сигналами, фиксируя моменты посылки сигнала, скажем, из точки А в точку В, отражения его в точке В и возвращения в точку А. Иными словами, под синхронизацией часов в СТО понимается установка для них некоторого нуль-пункта, а не выверка разности их хода. Последнее не требуется в силу того, что в СТО предполагается обусловленная равномерностью течения локального времени одинаковость хода идентичных часов в разных точках одной и той же инерциальной системы отсчета. Правда, ход часов меняется при ускоренных движениях, поэтому "расставлять" часы в инерциальной системе отсчета следует с большой осторожностью, а еще лучше предполагать (что обычно и делается), что идентичные часы изначально расположены в каждой точке инерциальной системы отсчета и не совершали никаких перемещений в пространстве.
В общей теории относительности (ОТО) ход часов в каждой точке пространства зависит от силы гравитационного поля, поэтому проблема равномерности времени становится значительно более сложной. В ОТО, несмотря на зависимость метрики времени от силы гравитационного поля, приходится считать, что в каждой точке пространства время течет равномерно. При этом предполагается, что если бы вдруг во всем пространстве исчезло гравитационное поле, то расположенные в каждой точке пространства часы стали бы идти одинаково.
Однако на чем основана подобная уверенность в том, что расположенные в разных точках пространства часы могут идти одинаково? По-видимому, только на одинаковости их устройства и изготовления (См, например: /Сивухин, 1989, с. 25/). Иными словами, предполагается, что длительность идентичных явлений одна и та же
/А. Пуанкаре/. Правда, А. Пуанкаре, высказывая сомнение по поводу такого постулата, имел в виду представление об абсолютной истинности этого постулата, тогда как в СТО и ОТО, казалось бы, указаны границы его истинности и выявлены факторы, от которых зависит истинность этого утверждения. Но тем не менее и в СТО остается нераскрытой природа равномерности времени и, в частности, одинаковости хода "идентичных" часов в разных точках одной и той же инерциальной системы отсчета.Вопрос о природе равномерности времени оказался настолько сложным, что и по сей день остается нерешенным.
Широкое распространение имеет представление о том, что все материальные процессы объективно делятся на два больших класса, а именно, на равномерные и неравномерные. При такой уникальности свойства равномерности уникальным становится и время, которое как бы “материализуется” этим единственным в своем роде потоком равномерных материальных процессов и вопрос о каком-либо исследовании свойства равномерности становится неразрешимым.
Весьма характерны в этом отношении рассуждения Дж. Уитроу. Приведя слова И. Ньютона о том, что “абсолютное, истинное математическое время само по себе и по самой своей сущности, без всякого отношения к чему-либо внешнему протекает равномерно и иначе называется длительностью”, Дж. Уитроу пишет, что это знаменитое определение времени было одним из самых критикуемых утверждений И. Ньютона. Это определение освящает время и представляет его в виде потока. Но “если бы время было чем-то текучим, то оно само состояло бы из ряда событий во времени, и это было бы бессмысленно. Более того, трудно также принять утверждение, будто время течет
“равномерно” или однородно, ибо это, по-видимому, означало бы, что имеется нечто, которое контролирует скорость потока времени таким образом, что она всегда одна и та же. Но если время можно рассматривать в изоляции “безотносительно к чему-либо внешнему”, какой смысл можно придать высказыванию, что скорость его течения постоянна? Если никакого смысла нельзя придать даже возможности неравномерного течения, то какое значение можно придать особому условию, что течение “равномерно”?” /Уитроу, 1964, с. 48/.Аналогичным образом рассуждает М.Д. Ахундов. Во-первых, пишет он, само рассмотрение течения времени уже есть представление времени как процесса во времени, а во-вторых, “трудно принять утверждение о равномерном течении времени, ибо это предполагает нечто контролирующее скорость потока времени. Если же время рассматривается
“без всякого отношения к чему-либо внешнему”, то какой смысл может иметь положение, что оно течет неравномерно” /Ахундов, 1974, с. 338/.Можно предположить, что подобного рода соображения препятствуют исследованиям этого "таинственного" свойства равномерности и выяснению его объективных и субъективных основ. Поэтому равномерность общеизвестного, измеряемого общепринятыми единицами физического времени до сих пор либо аксиоматически вводится (в порядке определения или даже просто пояснения понятия времени), либо негласно предполагается как само собой разумеющееся свойство времени. Поэтому неудивительно, что и сегодня многие исследователи считают, что "равномерность" не имеет под собой никакой объективной основы и что "равномерность" - это такое свойство эталонных часов, а следовательно и отмеряемого этими часами времени, которое устанавливается соглашением
.Разумеется, мы можем договориться считать равными интервалы времени между последующими повторениями любого повторяющегося процесса. Так, используя пример Р. Карнапа /Карнап, 1971/, мы можем по договоренности считать, что мистер Смит выходит из дома через равные интервалы времени, и по его выходам из дома измерять время. Вопрос только в том, какова ценность подобного способа измерения
времени. Не следует, видимо, забывать, что у А. Пуанкаре под "удобством" того или иного способа измерения времени имеется в виду не бытовая комфортность приемов и методов процесса измерения, а степень простоты формулировок законов физики, механики и астрономии, которую обеспечивают эти способы измерения времени (См. :/Пуанкаре, 1990, с. 232/).Все это не только общеизвестно, но и общепринято. Даже те авторы, которые считают, что равномерность эталонных часов устанавливается по соглашению, далеко не произвольным образом выбирают эталонные часы, а сохраняют в качестве эталонных именно те, которые уже отобраны человечеством на практике и которые как раз и обеспечивают наиболее простую "формулировку естественных законов" природы /А. Пуанкаре/. При этом, однако, удивительным образом не замечается то обстоятельство, что "часами", обеспечивающими подобного рода "удобство", неизменно являются движения или процессы, относящиеся к обширному классу "равномерных" движений и процессов, которые, как писали Л. Эйлер и Ж.-Л. д
’Аламбер, по самой их природе весьма существенно отличаются от неравномерных.Как мы уже отметили, Ж.-Л. д
’Аламбер указал на одно очень важное свойство именно равномерных движений, заключающееся в том, что отношение расстояний, пройденных двумя равномерно движущимися телами за один и тот же интервал времени, оказывается величиной постоянной для любых произвольно выбранных (не равных нулю) интервалов длительности.Однако этот критерий равномерности многими исследователями не принимается во внимание. Это объясняется тем, что до сих пор остается невыясненной природа равномерности, и равномерность сохраняет статус интуитивно понятного и не требующего объяснения свойства времени. При этом, как мы видели, до сих пор широкое распространение имеет представление о том, что равномерность - это вовсе не объективное свойство времени, а чисто условное, которое мы приписываем тем движениям или процессам, которые выбрали в качестве эталонных (основных) часов и по которым градуируются все остальные часы. Однако если принять последнюю точку зрения, то становится непонятной проблема точности измерения времени, успешным решением которой не без оснований гордится современная наука. Действительно, что означает точность измерения времени, если можно договориться считать равномерным любой процесс и сделать его эталонным? В этом случае под точностью измерения времени придется понимать только то, насколько точно часы, которыми мы пользуемся, воспроизводят ход наших эталонных часов и ничего более. Вместе с тем реальное положение дел в области измерения времени совершенно не допускает подобного произвола.
Равномерность как соотносительное свойство
материальных процессов. Роль классов соравномерных
процессов в метризации времени
Д'Аламбер, как и Ньютон, считал, что “время по своей природе течет равномерно” /Даламбер, 1950, с. 19/, но поскольку мы не можем непосредственно воспринимать время, то вынуждены для его измерения прибегать к чувственно воспринимаемым движениям, причем для этой цели в принципе пригодны любые, в том числе и неравномерные движения. Однако, замечает д
’Аламбер, “при помощи неравномерного движения невозможно было бы измерять время, не зная откуда-нибудь заранее, какая связь между отношением времен и отношением пройденных путей соответствует данному движению” /Там же, с.46/. Для того, чтобы использовать неравномерное движение для измерения времени, необходимо знать уравнение этого движения, которое можно рассматривать как уравнение, выражающее “не соотношение между пространством и временем...”, а “соотношение между отношением частей времени к единице времени и отношением частей пройденного пространства к единице пространства” /Там же, с.19/. Но уравнение движения, отмечает д’Аламбер, мы можем знать только из опыта, который предполагает, “что уже имеется вполне определенная мера времени” /Там же, с.46/.Поэтому для измерения времени мы должны искать “такой частный вид движения, при котором связь между отношением промежутков времени и отношением пройденного пути известна независимо от каких бы то ни было допущений, а просто в силу природы самого движения” /Там же, с.45/. А поскольку “длительность или продолжительность существования вещей одна и та же, быстры ли движения (по которым измеряется время), медленны ли, или их совсем нет...” /Ньютон, 1989, с.32/, а “абсолютное время” едино для всех вещей и движений, то искомый частный вид движения, по мнению д
’Аламбера, должен быть единственным, обладающим указанным выше свойством. “Обоим этим условиям (т.е. требованию априорной известности уравнения движения и условию единственности. - И.Х.) удовлетворяет только равномерное движение” /Даламбер, 1950, с.45/.“В самом деле, - рассуждает д
’Аламбер, - движение тела само по себе будет равномерным...: ускоренным или замедленным оно становится лишь при действии той или иной внешней причины, и тогда это движение может подчиняться бесчисленному множеству законов изменения. Закон равномерности, т.е. равенство отношения между промежутками времени и отношения между пройденными путями, является свойством этого движения, взятого само по себе. Поэтому равномерное движение имеет наибольшее соответствие с длительностью, и вследствие этого оно наиболее пригодно служить мерой этой длительности, поскольку части последней следуют одна за другой также неизменно и равномерно. Напротив, всякий закон ускорения или замедления движения, так сказать, произволен и зависит от внешних обстоятельств. Неравномерное движение не может быть, поэтому, естественной мерой времени” /Там же, с.46/.Каким же образом убедиться в том, что данное движение является абсолютно равномерным? Вслед за Ньютоном, который предполагал, что, может быть, и “не существует (в природе) такого равномерного движения, которым время могло бы измеряться с совершенною точностью” /Ньютон, 1989, с.32/, д
’Аламбер также склоняется к мысли, что, видимо, нельзя найти в точности равномерного движения. “Но, - пишет он, - отсюда вовсе не следует, что равномерное движение не является по своей природе единственной первичной и простейшей мерой времени. Если у нас нет возможности найти точную и строгую меру времени, то мы должны искать, по крайней мере, приближенную меру, - среди движений примерно равномерных” /Там же, с.46/.Итак, "равномерность" рассматривается д'Аламбером как абсолютное свойство некоторого единственного класса движений, в силу чего все наблюдаемые процессы предполагается возможным однозначно разбить на "равномерные" (или, по крайней мере, "приближенно равномерные") и неравномерные. Поэтому мы вправе ожидать, что даламберовские критерии равномерности помимо разделения всех движений на "равномерные" и "неравномерные", позволяют обеспечить также однозначность подобного разбиения.
Приступая к анализу предлагаемых Ж. д'Аламбером трех способов определения равномерности тех или иных движений, мы должны особо подчеркнуть, что все способы предполагают сравнение между собой двух или нескольких движений (процессов). Эта особенность даламберовских критериев далеко не случайна. Дело в том, что если нам дан один единственный процесс, то мы ничего не сможем сказать о его равномерности или неравномерности, поскольку для этого должны будем сравнивать между собой периоды времени, на протяжении которых наблюдаемая нами система изменяется одинаковым образом. Но эти периоды времени невозможно сравнивать между собой непосредственно, поскольку они следуют друг за другом во времени. Для решения нашей задачи мы должны были бы иметь некоторый "хранитель длительности", т.е. некоторые "часы", при помощи которых можно было бы сравнивать различные интервалы длительности. Но подобный "хранитель длительности" сам должен быть некоторым процессом, что противоречит нашему условию. Следовательно, вопрос о равномерности или неравномерности тех или иных процессов правомерен лишь в том случае, если мы имеем возможность сравнивать исследуемый процесс с другими материальными процессами. В этом случае мы можем воспользоваться следующим критерием равномерности:
“...Движение можно считать приближенно равномерным, когда мы, сравнивая его с другими движениями, замечаем, что все они управляются одним и тем же законом. Так, если несколько тел движутся таким образом, что пути, проходимые ими за одно и то же время, всегда находятся (точно или приближенно) в одном и том же отношении друг к другу, то считают движение этих тел равномерным или по меньшей мере весьма близким к равномерному” /Даламбер, 1950, с.47/. И далее д
’Аламбер следующим образом поясняет эту мысль.Пусть мы имеем равномерно движущееся тело А, которое за произвольно взятый промежуток времени Т проходит путь Е, а другое тело В, которое также движется равномерно, за тот же промежуток времени проходит расстояние е. “Тогда независимо от того, одновременно ли начали двигаться эти два тела или нет, отношение Е к е будет всегда одним и тем же. И этим свойством обладает лишь равномерное движение” /Там же, с.47/.
Однако нетрудно заметить, что если сравниваемые между собой равномерно движущиеся тела синхронно с одним и тем же коэффициентом К(
t) ускоряют и замедляют свое движение, то движения этих тел, даже став таким образом неравномерными, не перестанут удовлетворять критерию равномерности д’Аламбера.Действительно, если два тела, движущиеся равномерно, т.е. с постоянными скоростями а и
b, с некоторого момента начали с одним и тем же коэффициентом К(t) изменять свои скорости, и их скорости стали переменными величинами а*К(t) и b*K(t), то расстояния 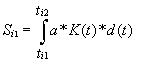 и
и 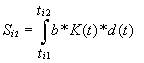 ,
,
и отношение
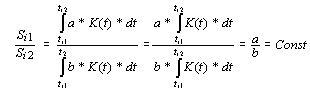
Таким образом, предположение д
’Аламбера о том, что свойством равномерности обладает один единственный класс движений, будет справедливым лишь в том случае, если сравниваемые движения не могут синхронно и совершенно одинаковым образом менять свои скорости. Если же предположить, что наблюдаемые процессы взаимосвязаны (скажем, через какие-то фундаментальные законы той или иной формы движения материи, к которой относятся сравниваемые процессы, или в силу принадлежности сравниваемых процессов к некоторой единой целостной системе, либо в силу каких-то иных причин) и совершенно одинаковым образом изменяют свои скорости, то мы должны прийти к выводу, что рассматриваемый критерий равномерности не дает возможности выделить из всего многообразия материальных процессов "истинно" равномерные, а лишь указывает на соравномерность сравниваемых процессов, т.е. на то, что данные процессы подчиняются одному и тому же (или одним и тем же) закону (или законам) и синхронно изменяют свои скорости одинаковым образом.Не позволяют установить "абсолютную равномерность" и два других предлагаемых д'Аламбером критерия равномерности.
Согласно одному из них, “...движение тела можно считать приближенно равномерным в том случае, если тело проходит одинаковые пути за такие промежутки времени, которые мы можем считать одинаковыми. Промежутки же времени мы можем считать одинаковыми в том случае, если многократные наблюдения показывают, что в течение их происходят одинаковые события, которые можно считать длящимися одинаково. Так, мы можем считать, что из одной и той же клепсидры вода вытекает всякий раз за одно и то же время” /Там же, с.47/.
Для того чтобы применять этот критерий равномерности, надо быть уверенным, что существуют процессы, протекающие всякий раз одинаково, при помощи которых можно отождествлять удаленные друг от друга (во времени) временные интервалы. Однако вывод о том, что данный процесс всякий раз протекает одинаково, опирается на наш повседневный опыт и основан, в конечном итоге, на сравнении этого процесса с другими. Но какова гарантия того, что сравниваемые процессы не связаны между собой какими-либо не известными нам фундаментальными законами природы и не входят в один и тот же класс соравномерных процессов?
Аналогичное возражение можно высказать и по отношению к третьему критерию равномерности, согласно которому “...движение можно считать приближенно равномерным, когда мы вправе полагать, что действие ускоряющей или замедляющей причины - если таковая имеется, - может быть только неощутимой” /Там же, с.47/.
Однако, в общем случае, о наличии или отсутствии подобных причин мы можем судить лишь по результатам их действия, т.е. по реальному ускорению или замедлению наблюдаемого движения или процесса, что также требует сопоставления исследуемых объектов с объектами, которые, по нашему мнению, либо не претерпевают никаких изменений, либо одинаковые изменения всякий раз длятся одинаково. Но в таком случае все те причины, которые одинаково ускоряют или замедляют все сравниваемые процессы, останутся для нас "неощутимыми".
Таким образом, предложенные Ж. д'Аламбером критерии равномерности основаны на сравнении двух или нескольких процессов между собой и позволяют установить лишь их соотносительную равномерность, т.е. их соравномерность относительно друг друга.
Рассмотрим теперь предложенный Рудольфом Карнапом (1891-1970) способ выделения пригодных для измерения времени строго периодических процессов.
Обсуждая вопрос о способах измерения времени, Р. Карнап обращается к периодическим процессам, среди которых различает "слабые периодические процессы", такие, как выходы мистера Смита из дома, пульс человека и т.п., т.е. процессы, у которых периоды могут каким-то образом изменяться, и "сильные периодические процессы", у которых периоды сохраняются постоянными. Для измерения времени желательно было бы взять такой периодический процесс, периоды которого всегда оставались бы неизменными. Но если мы еще не умеем измерять время, то мы и не можем априори сказать, какие периодические процессы относятся к слабым, а какие - к сильным.
Рудольф Карнап рассуждает следующим образом.
Представим себе, что мы живем на самых ранних этапах развития понятия измерения, не имеем инструментов для измерения времени и, разумеется, не знаем никаких законов материальных процессов. В этих условиях мы, во-первых, не можем складывать интервалы длительности, если только конец одного не совпадает с началом другого, и, во-вторых, не можем сравнивать между собой следующие друг за другом интервалы длительности. Для того чтобы иметь возможность сравнивать различные интервалы между собой и складывать их друг с другом, необходимо научиться измерять эти интервалы длительности. Поскольку у нас нет никакой возможности отличить “сильные” периодические процессы от “слабых”, мы можем для измерения времени выбрать любой периодический процесс, скажем, биение собственного пульса. Полагая, что удары сердца следуют через равные интервалы длительности, мы можем уже сказать, сколько ударов сердца содержат разные интервалы длительности, и таким образом сравнивать их между собой и складывать друг с другом. Но при этом окружающий мир будет несколько странным образом зависеть от состояния моего организма и от моего самочувствия: если я пробежался или меня бьет лихорадка, солнце начинает проходить свой путь за большее число ударов моего сердца, чем при спокойном состоянии моего организма и хорошем самочувствии. Перебирая для измерения времени разные периодические процессы, можно заметить, что если измерять время при помощи колебаний какого-либо маятника, то многие материальные процессы начинают вести себя более однообразно и выясняется большой класс эквивалентных периодических процессов, т.е. таких, длительности которых оказываются либо кратными с постоянным коэффициентом кратности длительности периода того маятника, при помощи которого мы измеряем время, либо составляют его определенную долю. При этом эквивалентные периодические процессы Р. Карнап определяет как такие процессы, у которых “…некоторое число периодов процесса
Таким образом, с точки зрения Р. Карнапа, время можно измерять при помощи любого периодического процесса. Предпочтение физическим маятникам следует отдать только потому, что, измеряя время при их помощи, мы получаем более простые законы движения материальных тел. При этом оказывается, что все периодические процессы, эквивалентные колебаниям маятника, представляют собой “сильные” периодические процессы, или, другими словами, выделенный таким образом класс эквивалентности состоит из строго периодических процессов и единственен в своем роде, поскольку все другие классы эквивалентных периодических процессов либо совпадают с этим классом (как, например, классы, эквивалентные вращению Земли вокруг оси или ее обращению вокруг Солнца), либо не пересекаются (как, например, класс эквивалентности биению сердца).
Нетрудно заметить, что сформулированное Р. Карнапом условие эквивалентности периодических процессов соответствует даламберовскому критерию равномерности механических движений. Действительно, если отношение числа периодов
Учитывая это, мы впредь будем рассматривать строго периодические процессы как дискретные равномерные процессы, у которых равномерно нарастает число полных периодов. Поэтому строго периодические процессы условно можно было бы называть “равномерными периодическими процессами”
.Общепринятый способ измерения времени Р. Карнап считает основанным на том, что эмпирически выявлен большой класс эквивалентных периодических процессов, каждый из которых может быть использован для измерения времени. К этому классу относятся вращательные движения небесных тел, колебания маятников, движения балансирных колесиков часов и др. При этом Р. Карнап замечает, что, “насколько мы знаем, существует только один обширный класс такого рода” /с. 133/ (Выделено Р. Карнапом).
Если справедливы утверждения Ж.Л. д’Аламбера и Р. Карнапа о том, что существует один единственный класс равномерных и строго периодических процессов, то должна существовать единственная метрика времени. Но вместе с тем, как мы видим, равномерность и строгая периодичность – это соотносительные свойства сравниваемых между собой монотонных и периодических процессов и в принципе возможно существование неограниченного множества классов соравномерных и строго периодических процессов. При этом можно показать, что с любым из этих классов может быть связано равномерное время.
C этой целью смоделируем абсолютно синхронное и пропорциональное изменение скоростей равномерных процессов и ритмики строго периодических процессов и покажем, что с помощью критерия равномерности д’Аламбера и критерия строгой периодичности Карнапа можно среди всего многообразия процессов выявить классы соравномерных процессов.
Представим себе, что на плоской, достаточно широкой и неограниченно длинной ленте нанесена декартова система координат с осью абсцисс, направленной вдоль, и осью ординат - поперек ленты. Лента изготовлена из идеально эластичной пленки и может, не образуя складок и не разрываясь, неограниченно сжиматься и растягиваться вдоль оси абсцисс, оставаясь неизменной вдоль оси ординат, т.е. растяжения и сжатия пленки представляют собой непрерывное взаимнооднозначное (гомеоморфное) отображение, при котором на континууме числовой оси (оси абсцисс) не исчезают существующие и не возникают новые точки, а также не меняется порядок их следования вдоль оси. Пленка, из которой сделана лента, может находиться и в фиксированном, как бы "замороженном", состоянии, когда она полностью теряет свою эластичность и становится абсолютно жесткой, недеформируемой;
- Представим далее, что мы зафиксировали ("заморозили") ленту в некотором исходном состоянии, нанесли на ось абсцисс равномерную шкалу (назовем ее шкалой q-времени) и, используя ее как шкалу времени, нанесли на ленту множество самых различных графиков, считая деления на оси ординат шкалами некоторых изменяющихся во времени величин. При этом пусть графики ![]() представляют собой графики равномерных,
представляют собой графики равномерных, ![]() - строго периодических и графики
- строго периодических и графики ![]() - более сложных и в том числе стохастических функций равномерного аргумента q;
- более сложных и в том числе стохастических функций равномерного аргумента q;
- Представим теперь, что лента "разморожена" и по всей длине оси абсцисс деформирована так, что в каждой точке этой оси коэффициент деформации К(
q) является случайной величиной. После этого мы снова зафиксировали ("заморозили") ленту, на ось абсцисс нанесли новую равномерную шкалу (назовем ее шкалой r-времени) и, используя ее как шкалу равномерного времени, нанесли на ленту новое множество графиков, среди которых графики- Предположим, что мы большое число раз проделали описанные выше операции "замораживания" и "размораживания" пленки и каждый раз наносили на ленту новые множества графиков, среди которых были как равномерные, так и строго периодические и более сложные функции наносимого каждый раз на
ось абсцисс равномерного времени. Обозначим последнюю нанесенную на ось абсцисс шкалу как шкалу t-времени, а графики равномерных функций обозначим- И, наконец, представим себе, что все нанесенные на ось абсцисс шкалы исчезли или настолько перепутались, что мы ими воспользоваться не можем; что у нас нет никакой линейки, при помощи которой можно было бы установить равенство различных отрезков на оси абсцисс; что мы не знаем, в каком состоянии находится наша пленка, и нам неизвестно, подвергалась ли она каким-либо сжатиям и растяжениям после того, как были нанесены последняя равномерная t-шкала и последнее множество графиков.
Итак, мы имеем на ленте огромное количество различных графиков, которые после их нанесения на ленту многократно деформировались вместе с лентой. Хотя мы не можем априори установить, какие графики и когда были нанесены - в этом отношении графики для нас неразличимы, - тем не менее для удобства рассуждений сохраним их обозначения, пометив только штрихами в знак того, что исследуемые графики отличаются от исходных в силу тех деформаций, которые испытала пленка после нанесения на нее каждого очередного множества графиков.
Для простоты дальнейших рассуждений мы рассмотрим только две первые группы графиков, т.е.
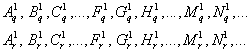
Покажем, что, используя первый критерий равномерности д
’Аламбера, мы можем среди этого множества графиков выделить две группы равномерных (и строго периодических) процессов и с определенной степенью точности восстановить исходные равномерные q- и r-шкалы на оси абсцисс, если в качестве конгруэнтной единицы деления возьмем период одного из строго периодических процессов первой группы ( q-шкала) или второй группы ( r-шкала).Выделим из всего многообразия функций все монотонные функции, в число которых, помимо функций, обозначенных литерами А, В, С, … , изначально равномерных функций, попадут и некоторые монотонные, но изначально неравномерные функции, находящиеся среди функций, обозначенные литерами М,
N, … . 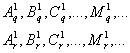
На произвольных отрезках оси абсцисс
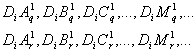
Если теперь найдем все попарные отношения этих величин и сравним их между собой, то обнаружим две группы функций, в каждой из которых отношения приростов функций на всех выделенных интервалах длительности оси абсцисс
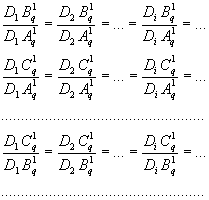
и
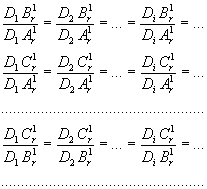
Но отношения приростов функций, принадлежащих разным группам, т.е. такие, как:
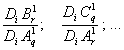
на разных интервалах оси абсцисс
Аналогичным образом можно рассмотреть группу повторяющихся (периодических) процессов:
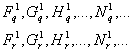
но при этом в качестве приростов функций на интервалах
Полученные результаты означают, что равномерную шкалу времени на оси абсцисс можно восстановить, выбрав в качестве строго периодического процесса один из эквивалентных процессов, выявленных либо среди периодических процессов
Если в качестве единицы измерения времени мы выберем периоды, скажем, функции
Можно показать, что с переходом к
Действительно, пусть до деформации ленты за время
И наконец, следует заметить, что квантованностью и точечностью
Что касается функций, графики которых были начерчены на ленте после ее деформации, то с переходом к
Аналогичным образом можно было бы рассмотреть любые группы выявленных повторяющихся (квазипериодических) процессов с другими индексами и "восстановить" на оси абсцисс соответствующие равномерные шкалы.
Разные классы соравномерных процессов как классы разных эквивалентностей не пересекаются между собой, поэтому если бы мы начали при помощи процессов того или иного класса измерять время, то все остальные классы соравномерных процессов потеряли бы для нас свойство “равномерности” и предстали бы в виде групп стохастических процессов.
В реальной действительности классы соравномерных и эквивалентных периодических процессов могут возникать в силу различных причин. Во-первых, они могут состоять из процессов, подчиняющихся одним и тем же фундаментальным законам. Во-вторых, подобный класс могут образовать процессы, принадлежащие такой целостной высокоинтегрированной материальной системе, в которой все процессы настолько тесно взаимосвязаны и сопряжены, что ведут себя как единый целостный поток, синхронно и пропорционально ускоряясь и замедляясь под воздействием разных, влияющих на данную систему факторов. И, наконец, в единый класс могут входить процессы, индуцированные одним и тем же фундаментальным процессом и строго повторяющие его ритмику.
Итак, равномерность представляет собой соотносительное свойство как минимум двух сопоставляемых между собой материальных процессов и в принципе возможно существование неограниченного множества классов соравномерных процессов
. При этом "критерии равномерности", которыми мы можем воспользоваться, не позволяют ни один из этих классов выделить как класс "истинной" или "абсолютной" равномерности. Что касается вопроса о реальном существовании качественно различных, не сводимых друг к другу классов соравномерных процессов, то современная наука, фактически, уже дала на него положительный ответ. Именно такими специфическими классами являются протекающие в живых организмах определенные совокупности биологических процессов, что позволяет, используя единицы биологического времени, описывать процессы жизнедеятельности и развития живых организмов не как стохастические, каковыми они выглядят при описании их в общепринятых единицах физического времени, а как динамические процессы.§ 2. Природа физического времени и характер соотношения
равномерности времени и закона сохранения энергии.
Анализ истории формирования идеи абсолютного времени классической физики привел нас к выводу, что ньютоновское “абсолютное, истинное математическое время” абстрагировано от суточного вращения Земли. Однако в силу ряда обстоятельств генетическая связь абсолютного времени с суточным вращением Земли вокруг оси оказалась основательно забытой и на протяжении более чем двух столетий после И. Ньютона в естествознании господствовало представление о времени как о некоторой равномерно текущей и ни от чего не зависящей субстанции.
С возникновением теории относительности физикам пришлось отказаться от идеи абсолютного времени. В современной физике общепринятым является предложенное А. Эйнштейном операциональное определение времени как измеряемого обычными часами физического параметра. Но такое определение времени сугубо феноменологично. Здесь, по сути дела, абсолютизируется общепринятый способ измерения времени и предлагается, не задаваясь метафизическими вопросами о природе и сущности времени, довольствоваться результатами его измерения
.При этом, однако, время превращается в чисто локальную характеристику мира, жестко привязанную к той точке мирового пространства, в которой находятся измеряющие время часы.
Для того чтобы преодолеть локальность измеряемого конкретными часами физического параметра “времени”, в специальной теории относительности (СТО) предполагается возможность существования в любой точке инерциальной системы отсчета стандартных часов, которые в силу идентичности своего устройства способны идти абсолютно одинаково, и вводится особая процедура “синхронизации” пространственно разобщенных часов. Таким образом, в СТО удается ввести представление о едином времени данной инерциальной системы отсчета.
Онтологическая неопределенность введенного таким образом понятия времени большинством естествоиспытателей, и в том числе физиков, преодолевается не всегда осознаваемыми квазиньютоновскими представлениями о времени как о некотором повсеместно происходящем в объективном мире равномерном движении. Но то обстоятельство, что это “равномерное течение”, т.е. “время”, непременно измеряется “секундами”, представляющими собой одну из шести фундаментальных единиц общепринятой Международной системы единиц физических величин СИ, свидетельствует о том, что выявленная нами генетическая связь абсолютного времени классической физики с суточным вращением Земли остается справедливой и для общепринятых ныне представлений о времени.
Дело в том, что “секунда” до 1956 года определялась как 1/86 400 часть средних солнечных суток. Однако в 50-х годах с помощью кварцевых часов была выявлена неравномерность вращения Земли вокруг оси, происходящая из-за сезонных перераспределений водных и воздушных масс Земли и других причин. Поэтому было принято новое определение “секунды” через период обращения Земли вокруг Солнца как 1/31 556 925, 9747 часть определенного тропического года. Правда, в 1967 году
XIII Международная конференция по мерам и весам связала единицу измерения времени с атомным стандартом и определила секунду как 9 192 631 770 периодов излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния цезия-133, но, как совершенно справедливо замечает А.Б. Щеголь, “единица осталась той же, но найден способ более точного и надежного воспроизведения” /Щеголь, 1988, с. 14/.Таким образом, хронометрируя тот или иной процесс или теоретически описывая его “во времени”, мы, по сути дела, как и во времена И. Ньютона, продолжаем сравнивать его с вращением Земли вокруг оси или с обращением ее вокруг Солнца и анализировать характер отклонений от соравномерности с указанными механическими движениями. Именно такой способ измерения времени и временного описания исследуемых процессов лежит в основе познания многих закономерностей материального мира.
Чем же обусловлена столь великая роль вращения Земли вокруг оси и обращения ее вокруг Солнца – этих механических движений – в познании законов природы?
Вращение Земли вокруг оси и ее обращение вокруг Солнца входят в весьма обширный класс соравномерных процессов, к которому, помимо вращательных движений небесных тел и космических систем типа Солнечной, относятся прямолинейные инерциальные движения масс в инерциальных системах отсчета, колебательные движения физических маятников, кристаллических, молекулярных и атомных осцилляторов. Все эти движения являются движениями закрытых консервативных динамических систем, т.е. таких систем, которые не обмениваются с окружающей средой массой и энергией и у которых в процессе движения сохраняется постоянной механическая энергия, или энергия движения. Именно сохранение неизменной величины механической энергии приводит к тому, что эти движения могут неограниченно долго длиться без каких-либо изменений характеристик, что и обусловливает их объединение в один класс соравномерных процессов. При этом говорить о соравномерности позволяет то обстоятельство, что в каждом из них имеется, по крайней мере, один параметр, величина которого нарастает равномерно “во времени”, если только “время” измеряется одним из входящих в этот класс “равномерных” или “строго периодических” процессов. Так, при прямолинейном инерциальном движении масс в инерциальной системе отсчета равномерно нарастает длина пройденного пути; при свободном “твердотельном” вращении небесного тела аналогичным образом нарастает угол поворота, а также число полных оборотов тела вокруг оси; при обращении одного небесного тела вокруг другого в таких космических системах, как Солнечная система, равномерно нарастает, во-первых, величина площади, заметаемой радиусом-вектором орбиты данной планеты, а во-вторых, число полных оборотов планеты вокруг центрального тела; у физических маятников, как и у других колебательных систем, равномерно “во времени” нарастает число полных периодов колебаний.
Рассматриваемый класс соравномерных процессов мы будем условно именовать классом “инерциально-равномерных” движений
.Таким образом, равномерность общеизвестного времени обусловлена тем, что оно измеряется при помощи таких закрытых динамических систем, у которых механическая энергия в процессе движения сохраняется постоянной. Более лаконично данный вывод можно сформулировать следующим образом: равномерность времени обусловлена законом сохранения (механической) энергии. Однако такой вывод находится в явном противоречии с широко распространенным представлением о том, что основные законы сохранения классической физики, и в том числе закон сохранения энергии, являются следствиями свойств симметрии пространства и времени.
В современной физике такая точка зрения на характер соотношения однородности (или, иначе, равномерности) времени и закона сохранения энергии общепринята, не подвергается сомнению и в учебных пособиях по физике для вузов излагается как незыблемая истина. “Метрические свойства пространства и времени - однородность и изотропность, - пишут авторы одного из учебников для вузов, - обусловливают фундаментальнейшие законы природы, имеющие решающее значение для всех разделов физики, а именно, следствием однородности пространства является закон сохранения импульса, изотропности - закон сохранения момента импульса, а следствием однородности времени - закон сохранения энергии” /Наркевич и др., 1992, с. 225/. Аналогичная точка зрения содержится и в других учебных пособиях (см., например: /Ландау , Лифшиц, 1989, с. 45, 61, 109/). Вслед за физиками такого же мнения придерживаются и многие философы. См, например: /Ахундов, 1982 а, с. 176/.
Справедливости ради следует отметить, что в ходе дискуссии по проблеме взаимосвязи и соотношения свойств симметрии пространства и времени и основных законов сохранения механики, состоявшейся среди отечественных философов в 60-70-е годы, отстаивались и иные точки зрения. Так, например, Н.Ф. Овчинников и Ю.Б. Румер обосновывали мнение, согласно которому не законы сохранения следуют из симметрии пространства и времени, а наоборот, законы сохранения обусловливают свойства симметрии пространства и времени (см.: /Овчинников, 1960, с. 177; Румер, Овчинников, 1968; Румер, 1971/). Ряд авторов, исходя из общефилософских соображений, доказывали, что поскольку пространство, время и движение суть основные однородные атрибуты материи, то “формы симметрии и соответствующие им законы сохранения в рамках существующей между ними связи” следует рассматривать “не в плане причинно-следственных отношений, а как однопорядковые, но различные стороны единой закономерности материального мира” /Абасов, 1980, с. 74/. Аналогичную точку зрения отстаивали В.С. Готт, А.Ф. Перетурин, А.Н. Шатохин и др. (См.: /Готт, 1972; Перетурин, Сидоров, 1968; Шатохин, 1968/).
Распространенность представления о том, что закон сохранения энергии обусловлен однородностью времени, объясняется прежде всего идущей со времен становления классической физики традицией выводить законы сохранения из общих аксиом движения. Эта традиция, как отмечают Ю.Б. Румер и Н.Ф. Овчинников /Румер, Овчинников, 1968/, была обусловлена тем, что основными понятиями классической механики первоначально были пространство, время и масса, а понятия импульс, момент импульса и энергия появились позднее и на протяжении длительного времени не воспринимались как фундаментальные понятия механики. Соответственно и математический аппарат классической механики строился таким образом, что закономерности движения выводились из фундаментальных свойств пространства и времени. Лишь постепенно, в ходе дискуссий о мере движения и о сохранении количества движения появляется введенное Г. Лейбницем понятие “энергия” как некоторая сохраняющаяся “живая сила” /Лейбниц, 1908, с. 145/, в противовес ньютоновским и декартовским представлениям о мере движения и его сохранении
.Определенную дань традиционному решению вопроса о характере взаимосвязи свойств симметрии пространства и времени и законов сохранения классической физики отдала Эмми Нётер, которая, доказав возможность математического вывода всех законов сохранения из свойств симметрии динамических систем, казалось, окончательно подтвердила истинность традиционного решения рассматриваемой проблемы. Именно так были восприняты результаты исследований Э. Нётер большинством ученых в начале нашего столетия, и такая оценка ее знаменитой теоремы продолжает господствовать по настоящее время. Некоторым авторам кажется особенно сильным аргументом в пользу традиционных представлений то обстоятельство, что обратная теорема Нётер, как выяснилось, в общем случае несправедлива. Этим авторам дело представляется таким образом, будто прямая теорема Нётер устанавливает реально существующее в действительности следование законов сохранения из свойств симметрии пространства и времени. Поэтому для того, чтобы в реальной действительности свойства симметрии пространства и времени следовали из законов сохранения, считают они, должна быть справедлива обратная теорема Нётер, позволяющая из законов сохранения выводить свойства симметрии динамических систем. А поскольку обратная теорема Нётер в общем случае неверна, то отсюда, с их точки зрения, следует справедливость традиционных представлений о фундаментальности свойств симметрии пространства и времени по сравнению с соответствующими законами сохранения.
Однако теорема Нётер сама по себе не устанавливает никаких отношений субординации между свойствами симметрии динамических систем и законами сохранения физических величин, характеризующих движение этих систем, и тем более не указывает на существование каких-либо причинно-следственных связей между ними. В.С. Барашенков, обсуждая физический смысл прямой и обратной теорем Нётер, приходит к выводу, что согласно этим теоремам “каждому типу симметрии соответствует свой закон сохранения и, наоборот, каждому закону сохранения может быть сопоставлена вполне определенная симметрия. В рамках современных физических теорий нельзя установить, что является более фундаментальным - симметрия или же неразрывно связанный с ней закон сохранения” /Барашенков, 1980, с. 336/. Здесь мы имеем чисто математическую теорему, устанавливающую только функциональные связи и дающую в руки исследователей математический аппарат, позволяющий из свойств симметрии выводить законы сохранения. Но ни функциональные связи, существующие между теми или иными свойствами исследуемых объектов, ни возможность математического вывода характеристик или параметров одних свойств из характеристик или параметров других - сами по себе не свидетельствуют о каких-либо причинно-следственных связях или отношениях субординации. Для того, чтобы иметь возможность существующие между свойствами реальной действительности функциональные связи толковать как причинно-следственные, необходимо обратиться к самой реальной действительности и выяснить характер зависимостей, существующих между соответствующими свойствами ее объектов.
Содержательный анализ взаимосвязи однородности (равномерности) времени и закона сохранения энергии требует выяснения сущности того независимого физического параметра
t, который под названием “ время” фигурирует в физических теориях. В самой физике, как мы видели, понятие “ время” , по сути дела, не определяется, а параметр t вводится операционально. Существующие же философские концепции времени также не могут служить достаточным основанием для содержательного анализа взаимосвязи свойства однородности (или, точнее, равномерности) времени и закона сохранения энергии. Действительно, согласно современным представлениям, “время” – это либо некоторая неопределенной природы равномерно текущая сущность, либо некоторое столь фундаментальное свойство движущейся материи, что о нем нельзя сказать ничего более определенного, кроме как указать на связь с движением материи; либо сам процесс “становления” материального мира; либо, наконец, вовсе нечто сугубо субъективное, имеющее место в человеческом или в некотором Мировом, надчеловеческом сознании. Ни в одном из этих вариантов определения времени мы не можем найти даже намека на возможность содержательного анализа, во-первых, свойства равномерности и, во-вторых, характера взаимосвязи между свойством однородности (равномерности) времени и законом сохранения энергии. В такой ситуации поневоле приходится придерживаться традиционно сложившихся представлений о характере взаимосвязи между свойствами симметрии пространства и времени и основными законами сохранения классической физики.Физический смысл параметра
t раскрывается в том случае, если учесть, что самоконгруэнтные единицы физического времени задаются теми или иными “равномерными” или “строго периодическими” процессами класса “ инерциально-равномерных” движений. “ Физическое время” (физический параметр t) при этом оказывается метризованной при помощи класса “ инерциально-равномерных” движений длительностью бытия материальных процессов. Поскольку класс “ инерциально-равномерных” движений состоит из движений закрытых консервативных динамических систем, то можно утверждать, что соравномерность монотонных и эквивалентность периодических процессов этого класса, а следовательно, и равномерность физического времени, обусловлены тем, что движения закрытых консервативных систем неограниченно долго (в идеале) остаются неизменными в силу подчинения их закону сохранения (механической) энергии.И, наконец, отметим, что повышение точности измерения физического времени означает ничто иное, как использование в качестве часов таких динамических систем, которые все более строго удовлетворяют критериям закрытости и консервативности, а также выявление и учет факторов, нарушающих закрытость и консервативность динамических систем, используемых в качестве часов.
Веским аргументом в пользу представления о том, что время – это некий единый, вездесущий равномерный поток, является наша интуиция времени, которая проявляется в виде чувства равномерного дления и способности оценивать в общепринятых единицах различные интервалы длительности, не прибегая ни к каким материальным измерителям или индикаторам времени. Но можно показать, что присущее человеку чувство времени тесно связано с “биологическими часами”, которые эквивалентны циклическим процессам класса “инерциально-равномерных” движений.
Как известно, предпринятая еще в конце прошлого века попытка И.М. Сеченова (1829-1905) с позиций естественнонаучного материализма решить проблему восприятия человеком времени привела его к выводу о том, что объективное время человек воспринимает при помощи органов слуха, зрения и рецепторов мышечного ощущения. Он писал: “В самом деле, только звук и мышечное ощущение дают человеку представление о времени, притом не всем своим содержанием, а лишь одною стороною, тягучестью звука и тягучестью мышечного чувства. Перед моими глазами двигается предмет; следя за ним, я двигаю постепенно или головой, или глазами, или обоими вместе; во всяком случае зрительное ощущение ассоциируется с тянущимся ощущением сокращающихся мышц...” /Сеченов, 1952, т. 1, с. 77-78/. При решении вопроса о механизмах восприятия времени отечественные философы и психологи продолжают опираться на выводы И.М. Сеченова. Так, например, Н.И. Моисеева, изложив приведенные выше представления И.М. Сеченова, пишет: “Для отсчета временных отношений важно мышечное чувство с его “тягучестью в сознании” не только само по себе и не столько статическое мышечное чувство, а те ощущения, которые сопутствуют двигательной активности, особенно ходьба, представляющая, по И.М. Сеченову, “шаблон”, на котором могли развиваться числа, линейная мера и мера времени, поскольку шаги представляют собой ряд повторных действий с постоянной продолжительностью и паузами. Сопровождающее их мышечное чувство может служить “измерителем или дробным анализатором пространства и времени” /Моисеева, 1989, с. 263/. Автор, разумеется, знает о существовании “биологических часов” и признает, что организм располагает собственным внутренним механизмом отсчета времени, но считает, что “подсчеты по этой системе наименее точны, что выявлено в многочисленных опытах с сенсорной депривацией, когда человек ориентировался во времени исключительно по собственному внутреннему чувству” /Там же, с. 267/.
Аналогичным образом решает вопрос о механизмах восприятия времени Н.Д. Багрова. “По современным представлениям, - пишет она, - у человека нет специального временного анализатора, равнозначного по физиологическому смыслу зрительному или слуховому... Вместе с тем каждый анализатор наряду со своей непосредственной функцией может при определенных условиях выполнять еще и функцию отсчета времени... Однако собран большой экспериментальный материал, свидетельствующий о том, что слуховой анализатор точнее других определяет время” /Багрова, 1980, с. 18/.
Выясняя механизмы чувства (интуиции) времени, следует особое внимание обратить на то, что способность “воспринимать и оценивать время” не является приобретением человека, а получена им по наследству от его животных предков и что в основе этой способности лежат механизмы так называемого “опережающего отражения”. Разумеется, было бы совершенно неверно предполагать, что живые организмы эмоционально переживают и тем более осознают свое “восприятие” и “оценку” времени. Здесь мы имеем дело со своего рода “часовыми механизмами”, приспосабливающими течение физиологических процессов живых организмов, а также их поведение и деятельность к течению физического времени. Такими “часовыми механизмами” и являются “биологические часы”, представляющие собой сложные иерархически организованные системы периодических (или колебательных) биологических процессов, периоды которых с определенной степенью точности и постоянства эквивалентны (в смысле Р. Карнапа) периодам суточных, месячных и сезонных (годовых) изменений условий их обитания.
В настоящее время имеются убедительные факты, свидетельствующие о том, что объективное физическое время человек воспринимает не непосредственно, как нечто объективно существующее во внешнем материальном мире и воздействующее на те или иные органы чувств, а опосредованно, через субъективное переживание своего собственного бытия. При этом периоды тех или иных ритмических процессов “биологических часов” собственного организма ощущаются и осознаются им как равные интервалы длительности.
Многочисленные эксперименты свидетельствуют о том, что, будучи изолированным от циклических изменений окружающих условий (например, находясь в сурдокамере или глубокой пещере), человек оказывается не в состоянии “воспринимать и оценивать” “равномерно текущее объективное время”. Более того, на протяжении всего эксперимента он остается уверенным, что его субъективные сутки, т.е. длительности периодов “сон-бодрствование”, не претерпевают сколь-либо существенных изменений и остаются равными приблизительно 24 часам, тогда как на самом деле продолжительность его субъективных суток оказывается подверженной случайным изменениям и имеет тенденцию растягиваться до 48 часов.
О том, что субъективное чувство равномерного дления связано не с восприятием извне равномерно текущего объективного времени, а с субъективным переживанием протекающего в организме самого человека потока биологических процессов, среди которых важную роль играют циклические процессы “биологических часов”, свидетельствуют и другие факты. Так, изменение общей ритмики биологических процессов организма (например, при резких нарушениях температуры тела) человек воспринимает и переживает как изменение ритмики объективного физического времени.
“Очень вероятно, - пишет по этому поводу Дж. Уитроу, - что постоянная температура человеческого тела является решающим фактором, связывающим индивидуальное время человека с универсальным физическим временем и предохраняющим их взаимоотношение от излишней неустойчивости. Эта гипотеза была проверена Г. Хогландом
/Hoagland, 1935/, который в своем исследовании “химической основы нашего чувства времени” нашел, что эксперименты по оценке времени людьми с повышенной температурой подтверждают, что повышенная температура тела вынуждает химические часы идти быстрее и поэтому внешнее время кажется идущим медленнее” /Уитроу, 1964, с. 88/. Поэтому если бы человек был пойкилотермным (холоднокровным) живым существом и температура его тела весьма существенным образом зависела от температуры окружающей среды, то ему было бы весьма трудно представить себе, что окружающий физический мир существует в равномерном физическом времени, поскольку в этом случае человек воспринимал бы окружающую действительность так, как, по мнению Гудхардта, по-видимому, воспринимает мир ящерица, которой в жаркий солнечный день весь мир кажется живущим в замедленном ритме времени, а большая часть живых существ кажутся какими-то неуклюжими увальнями, тогда как в холодный пасмурный день материальные процессы внешнего мира начинают течь с повышенной скоростью, а большинство живых существ становятся чрезмерно подвижными и ловкими /Goodhart, 1957/.Отметим, что субъективное переживание человеком равномерного дления имеет два принципиально разных механизма, один из которых связан с рассматриваемыми нами “биологическими часами”, а другой, - с протекающими в мозгу и во всей нервной системе информационными процессами. В зависимости от обстоятельств чувство равномерного дления может быть связано с тем или другим механизмом субъективного чувства времени. Но и в том, и в другом случае изменение хода субъективного времени человеком переживается и осознается как изменение ритмики не субъективного, а объективного времени.
Укажем еще на один факт, свидетельствующий о том, что восприятие объективного времени зависит от ритмики протекающих в головном мозгу человека информационных процессов. Известно, что в стрессовых ситуациях у операторов сложных человеко-машинных систем иногда наблюдается резкое изменение ритмики информационных процессов и за очень короткий интервал физического времени они успевают проанализировать значительный объем информации и принять весьма ответственные решения /Береговой, 1979/. В нормальных условиях на всю эту работу потребовался бы значительно больший интервал физического времени. Однако субъективно человек переживает эту ситуацию не как ускорение каких-то процессов собственного организма, а как замедление или даже кратковременную остановку объективного физического времени. Поэтому не случайно в психологии подобная реакция операторов сложных человеко-машинных систем на стрессовую ситуацию получила наименование феномена “замедления” времени /Китаев-Смык, 1983, с. .206/.
И наконец, с механизмами “биологических часов” связана также способность человека интуитивно, не прибегая ни к каким внешним измерителям или индикаторам времени, оценивать в общепринятых единицах физического времени различные, в том числе небольшие, интервалы длительности.
Система “биологических часов” включает не только циркадные, месячные, сезонные и другие долгопериодические, но и большое количество короткопериодических колебательных (циклических) процессов, которые с определенной степенью точности и постоянства эквивалентны ритмическим изменениям внешних условий, что и делает их компонентами “биологических часов” физического времени, при помощи которых человек производит оценку длительности коротких интервалов времени. Но для этого периоды соответствующих колебательных процессов должны быть прокалиброваны в единицах физического времени. В современных условиях подобная калибровка короткопериодических компонент “биологических часов” происходит очень часто в процессе повседневного использования часов при оценке различных интервалов длительности. В результате у человека формируется способность достаточно точно оценивать длительности различных интервалов времени.
Таким образом, интуиция времени существует благодаря тому, что в организме человека имеется сложная система колебательных (циклических) процессов, эквивалентных таким периодическим процессам физического мира, как вращение Земли вокруг оси и ее обращение вокруг Солнца. Но это означает, что “биологические часы”, будучи эквивалентными указанным выше движениям класса “инерциально-равномерных”, сами как бы включаются в этот класс и таким образом “привязывают” и подчиняют протекающие в организме биологические процессы, а в конечном итоге поведение и жизнедеятельность, “равномерному течению” физического времени.
Итак, одним из весьма обширных и хорошо известных классов соравномерных процессов является совокупность материальных процессов, при помощи которых обычно измеряется время. Сюда относятся вращательные движения небесных тел вокруг собственных осей и общих центров масс в космических системах типа Солнечной, прямолинейные инерциальные движения масс в инерциальных системах отсчета, качания физических маятников в постоянном гравитационном поле и другие. Ядро этого класса составляют механические движения закрытых консервативных динамических систем, которые не обмениваются со средой веществом и энергией (закрытость) и у которых в процессе движения сохраняется постоянной энергия движения, или, иначе, механическая энергия (консервативность). Рассматриваемый класс соравномерных процессов условно назван классом “инерциально-равномерных” движений
.Именно постоянство энергии движения приводит к тому, что закрытые консервативные динамические системы могут неограниченно долго продолжать движение без изменения его характеристик и тем самым сохранять соравномерность с другими движениями этого класса. Но это означает, что не закон сохранения энергии является следствием однородности (равномерности) времени, как это принято считать, а наоборот, свойство равномерности времени, измеряемого “инерциально-равномерными” движениями, является следствием закона сохранения (механической) энергии.
§ 3. Специфика временной организации биологических процессов
и характер взаимосвязи биологического и физического времени.
Трюизмом звучит тезис о том, что решить загадку жизни - это познать жизнь как особую форму движения материи. Однако в этом тезисе заключен глубокий смысл, связанный с тем, что ни в одной области материальной действительности движение - непрерывные изменения состава, структуры и состояний объектов - не имеет столь важного значения, как в живой материи. Можно
c полным правом утверждать, что сущность жизни - в ее непрерывном движении. Поэтому раскрыть сущность жизни - это значит раскрыть временную структуру биологических процессов, познать законы временной организации процессов функционирования и развития живых организмов и, в конечном итоге, научиться математически описывать жизнь как особое движение материи.Серьезным препятствием на пути решения этой задачи является преобладание в живой материи стохастических процессов, требующих для своего описания статистических и вероятностных методов, тогда как в современной науке имеются многочисленные факты, свидетельствующие о том, что развитие организмов, а следовательно, и обеспечивающие это развитие биологические процессы, подчиняются каким-то неизвестным науке динамическим законам, которые скрыты за внешней стохастичностью процессов.
В этом отношении большой интерес представляют работы тех биологов, которые хронометрируют исследуемые процессы не в астрономических единицах физического времени, а в особых единицах длительности, отмеряемых при помощи тех или иных процессов самого изучаемого живого организма. При таком способе хронометрирования обнаруживается удивительное единообразие в развитии организмов, говорящее о существовании внутренних динамических законов развития, которые не могут быть выявлены при использовании общепринятых единиц измерения времени.
Подобный способ временного описания не укладывается в рамки общепринятых представлений о времени. Поэтому даже сами биологи, использующие специфические единицы длительности, склонны рассматривать их не как единицы особого биологического времени, а как некоторые искусственно введенные безразмерные характеристики развития изучаемого живого организма.
Но выше было показано, что равномерность - это не абсолютное свойство одного единственного класса материальных процессов, а соотносительное, и что возможно существование неограниченного множества классов соравномерных процессов. В общем случае различные классы соравномерных процессов взаимно стохастичны. Поэтому можно предположить, что стохастичность биологических процессов в значительной степени обусловлена тем, что материальные процессы биологических систем, объективно структурированные в равномерном биологическом времени, мы хронометрируем и пытаемся теоретически описывать в физическом времени, единицы которого стохастичны по отношению к единицам биологического времени.
Существование биологического времени означает, что биологическая реальность живой материи качественно отличается от физической реальности неживой природы тем, что протекающие в живых организмах биологические процессы и связанные с этими процессами события структурированы в особом, качественно отличном от физического биологическом времени. Но если это так, то все экспериментальные и теоретические исследования живых организмов, протекающие в них биологические процессы, а также процессы их функционирования и развития необходимо вести в единицах биологического времени. Такой переход в биологии от физического к биологическому времени имеет для биологии весьма далеко идущие последствия, поскольку при этом потребуется пересмотреть многие общепринятые ныне представления и понятия. Так, например, с переходом от физического к биологическому времени потребуется разработать системы единиц биологических величин и системы биологических констант, поскольку все те производные физические величины и физические константы, в размерностях которых фигурирует размерность физического времени “секунда”, в единицах биологического времени превратятся в стохастические переменные величины, и появятся новые, сугубо биологические производные величины и константы, в размерностях которых будет находиться размерность биологического времени. Вполне естественно, что биологические процессы живого организма подчиняются не физическим законам, в формулировках которых присутствует независимая переменная “
t”, т.е. физическое время, а биологическим, в формулировках которых в качестве независимой переменной “τ” фигурирует биологическое время.Подобная смена парадигмы требует самого тщательного методологического анализа всего круга проблем, связанных с введением в понятийный аппарат биологии понятия биологическое время. Вполне естественно, что методологический анализ невозможен без определенного вторжения философии в пределы естествознания, но, в отличие от так называемого натурфилософского подхода, он не предполагает получения “готовых решений естественнонаучных проблем путем дедукции этих решений из философских принципов” /Бранский, 1989, с. 28/. Поэтому высказанные в настоящем параграфе соображения о наиболее фундаментальных единицах биологического времени следует воспринимать лишь как гипотезы, призванные помочь обосновать принципиальную возможность существования наиболее фундаментальных и единых для всех периодов развития живого организма “ квантов” биологического времени.
* * *
Живая материя отличается крайней противоречивостью, которая проявляется в виде удивительного сочетания в ней, во-первых, “поразительной устойчивости” с “тончайшей чувствительностью к изменениям” /Уотермен, 1968, с. 12/ и, во-вторых, невероятного многообразия живых организмов с однотипностью их строения и единством исходных принципов организации и функционирования.
В силу высокой чувствительности биологических систем к изменениям, при попытках математически описать биологические процессы приходится учитывать огромное число в большинстве своем случайно изменяющихся переменных, что вполне естественно приводит к использованию статистических и вероятностных методов описания. Зависимость биологических процессов от большого числа случайным образом изменяющихся переменных в сочетании с безграничным разнообразием форм жизни наводит некоторых исследователей на мысль о том, что в биологии, в отличие от физики, нет "абсолютных явлений"
.Но вместе с тем, как показали открытия середины
XX столетия в генетике, в биохимии и молекулярной биологии, в анатомии и физиологии клетки, живые организмы, начиная с микроорганизмов и кончая человеком, имеют в своей основе гораздо больше общего, чем можно было предполагать. Так, выяснилось, что они пользуются одним и тем же генетическим кодом для передачи наследственной информации, всеобщими оказались основные реакции клеточного обмена, а также многие внутриклеточные структуры. Подобного рода факты приводят к выводу, что наблюдаемое многообразие форм жизни является в значительной мере внешним и что в основу фантастического многообразия организмов Природой положено поразительно мало принципов /Грин, Голдбергер, 1968, с. 15/. Выявление этих принципов и построение на их основе теоретической биологии, способной количественно описывать как отдельные биологические процессы, так и поведение биологических систем в целом, признавались как наиболее актуальные проблемы науки. Многим исследователям казалось, что биология наконец-то приближается к построению такой теоретической дисциплины, которая по своим возможностям будет близка к теоретической физике.В это время благодаря развитию молекулярной биологии все более глубоко раскрывается фундаментальное значение клетки как основной структурной и функциональной единицы живых организмов и все более широкое признание получает представление о том, что решение многих общебиологических проблем может быть достигнуто лишь "на уровне клетки". Поэтому представлялось, что одним из важных этапов в создании теоретической биологии должно явиться построение математической модели клетки и внутриклеточных процессов.
Однако несмотря на огромные успехи ряда наук, занятых изучением клетки, теоретическая цитология была еще весьма далека от того, чтобы описывать клетку как “... материальное выражение некоего комплекса принципов механики, обладающее уникальной молекулярной архитектурой и организацией” /Грин, Гольдбергер, 1968, с.17/. Анализ же имевшихся в то время попыток создать математическую модель клетки и внутриклеточных процессов приводил исследователей к неутешительному выводу, что “нет сколько-нибудь реальной возможности создания математической модели клетки” /Молчанов А.М., 1967, с.3
08/.При рассмотрении причин, затруднявших математическое описание биологических систем, высказывалась даже мысль о том, что “объекты, изучаемые в биологии, чрезвычайно сложны, и сколько-нибудь адекватное их описание лежит, как правило, за пределами возможностей современной математики” /Гнеденко, Фомин, Хургин, 1962, с.103/, формировавшейся на основе количественного описания объектов и процессов неживой природы, и что к адекватному математическому описанию биологических систем и процессов можно будет приблизиться лишь тогда, когда будет разработан математический аппарат, соответствующий природе живой материи. Разумеется, успешное развитие теоретической биологии может привести к дальнейшему развитию самой математики, однако трудно согласиться с тем, что имевшийся в
60-х годах математический аппарат был недостаточно сложен (или универсален) и поэтому не пригоден для адекватного описания биологических систем и процессов. Неудачи математического описания таких биологических систем, как живая клетка, на наш взгляд, были обусловлены прежде всего неудовлетворительностью понятийного аппарата самой биологии, который в значительной мере состоял из понятий, механически перенесенных в биологию из наук о неживой природе и не отражавших специфики живой материи. Правы были те авторы, которые, говоря о необходимости развития теории клетки и внутриклеточных процессов, прежде всего подчеркивали важность теоретического обобщения достижений современной биологии. Наиболее четко эта мысль была выражена авторами монографии “Регуляторные механизмы клетки”, которые писали: “За последние два-три десятилетия биология накопила огромный фактический материал описательного характера. В то же время теоретическая биология, теоретические обобщения далеко не соответствуют возможностям, которые создаются благодаря наличию большого объема эмпирических знаний. Хотя проблемами биологии глубоко заинтересовались математики, кибернетики, физики и химики, их стремления в значительной мере сдерживаются тем, что современная теоретическая биология еще не обобщила, не систематизировала накопленный материал с определенной объединяющей позиции и не вскрыла наиболее общие черты строения всего живого, течения процессов жизнедеятельности, не подготовила почвы для моделирования сущности жизни” /Сытник, Кордюм, Кок, 1969, с.3/.В работах, посвященных изучению и описанию клетки и внутриклеточных связей и процессов, достаточно четко выделились два направления, одно из которых можно назвать структурно-функциональным, другое - феноменологическим.
Первое связано с детальным исследованием структуры клетки и внутриклеточных образований, конкретных физико-химических механизмов взаимодействия различных элементов внутриклеточной организации, каналов внутриклеточной коммуникации, физико-химических свойств материальных носителей информации, способов обмена информацией между отдельными элементами клеточной структуры и т.д.
Задачи данного направления достаточно четко были изложены в Предисловии книги "Механизмы интеграции клеточного обмена". "Проблема механизма интеграции, - писал автор Предисловия С. Нейфах, - это, в сущности, проблема конструкции системы. Нельзя понять конструкцию, если, разложив систему на элементарные части, не попытаться рассмотреть рабочие узлы и блоки этой системы и пролегающие между ними коммуникации. Для того чтобы проанализировать участие биокаталитической системы клетки в интеграции обмена, недостаточно знание только структуры и функций индивидуальных белков-ферментов как таковых. Необходимо установить также взаимосвязи между ферментами, способы регулирования их активности, механизм их репродукции и т.д." /Нейфах, 1967, с. /.
Разрабатывая это уже достаточно развитое к концу 60-х годов направление исследования, обычно предполагали, что, детально изучив отдельные компоненты клетки, выяснив и исследовав конкретные физико-химические механизмы внутриклеточных связей, можно будет в дальнейшем прийти к синтезу целого в виде некоторой идеальной модели "минимальной клетки". Предполагалось, что эта модель, обладая лишь минимумом необходимого для любой клетки оснащения, будет копировать с той или иной степенью точности (в зависимости от того, что признается "необходимым оснащением") материальную структуру клетки и отдельных ее элементов и позволит, наконец, понять функционирование живой клетки как целостной системы
.Познавательная ценность структурно-функционального направления заключалась в том, что оно давало богатый фактический материал о процессах, строении и функционировании клетки и отдельных ее элементов, тот материал, без которого невозможно выяснить специфику живой клетки как целостной системы и построить в конечном итоге ее математическую модель.
Однако, нацеливая на конкретно-эмпирическое исследование живой клетки, сторонники данного направления исходили из предположения, что отдельные внутриклеточные процессы, а также внутриклеточные взаимодействия подчиняются обычным физическим и физико-химическим законам и что загадка клетки как целостной интегрированной системы, равно как и вообще "секреты жизни", скрывается в неизвестных пока деталях организации клетки. Характеризуя подобного рода представления, Г. Патти писал: "... В последнее время, после так называемого молекулярно-биологического переворота, неоднократно высказывалось мнение, что теперь, наконец, загадка жизни сведена к языку и законам физики. В частности, как заявляют биохимики и молекулярные генетики, им удалось доказать, что обычные физические и химические законы дают относительно ясную и простую основу для понимания наследственности и большинства процессов обмена веществ. Модель матричной ДНК, предложенная Уотсоном и Криком, общепринята как главный ключ к загадке наследственности, подобно тому, как выяснение детальной структуры белков позволило в основном понять ферментативные механизмы. Обычное рабочее допущение молекулярных биологов заключается в том, что оставшиеся проблемы будут разрешены с помощью дополнительных экспериментов. Во всяком случае, они не видят перед собой никаких препятствий или принципиальных загадок. В результате возникает представление о том, что биология объяснима в рамках обычных физических законов и что поэтому приложение физической теории к живой материи не требует особых усилий" /Патти, 1970, с.71-72/.
Но предположение о том, что, не выходя за рамки существующих в современной физике и химии законов и теорий, можно достаточно адекватно описать и объяснить функционирование живой клетки и течение внутриклеточных процессов, неизбежно вело к абсолютизации этих законов и теорий и к формированию соответствующих модификаций механистических воззрений на жизнь. При этом необходимо подчеркнуть, что сущность механистического объяснения жизни, заключающаяся в попытках раскрыть секрет жизнедеятельности живых организмов оставаясь в пределах построенных на основе изучения неживой природы физических и химических теорий, не зависит от того, каковы сами по себе эти теории. Так, например, представление о том, что тайна жизни должна уложиться в рамки, установленные законами волновой механики, и что "эта тайна скрывается, очевидно, где-то в сфере электронных взаимодействий, происходящих либо на суб- или супрамолекулярном уровне, либо внутри самих молекул, либо между молекулами, участвующими в биохимических процессах... " /Пюльман, 1966, с.5/, в гносеологическим плане мало чем отличается от значительно более грубой, первоначальной формы механицизма, пытавшегося уложить тайну жизни в рамки законов классической механики. Причем достаточно последовательное развитие механистических представлений в биологии рано или поздно наталкивается на специфические особенности живой материи, не укладывающиеся в рамки используемых физических и химических законов и теорий, что вызывает стремление к идеалистической "компенсации" механистических "переупрощений" загадки жизни "с помощью постулирования разного рода витальных сил" /Фролов, 1972, с.93/. Иными словами, "... механицизм в биологии, какие бы формы он ни принимал в зависимости от абсолютизируемых им методов ("физицизм", "химизм" и пр.) "дополняется" идеалистическими конструкциями - неовитализмом, психоламаркизмом, холизмом, неофинализмом и пр., а то и прямой апелляцией к религии, к идее бога" /Там же/. Поэтому абсолютизация структурно-функционального направления, опирающегося в теоретическом плане на известные физические и химические законы и теории, оказывается сопряженной с опасностью распространения, с одной стороны, механистических тенденций в объяснении жизни, а с другой - идеалистических "дополнений" к механистическим представлениям о сущности жизни.
Итак, структурно-функциональное направление вело к накоплению данных о материальной структуре клетки и о внутриклеточных процессах, и в этом его огромная познавательная ценность. Однако было бы неправильно абсолютизировать данное направление в изучении клетки. Более того, двигаясь от материальной структуры к объяснению клетки как целостной системы, мы вряд ли сумеем представить происхождение самой клетки как необходимое следствие специфических особенностей биологических и, прежде всего, биохимических процессов. Утверждение о том, что "проблема механизмов интеграции клетки - это, в сущности, проблема конструкции системы", по отношению к такой системе, как живая клетка, справедливо лишь наполовину, поскольку сама конструкция системы должна быть естественным образом объяснена как неизбежный результат действия каких-то принципов самоорганизации биологических систем, которые, в свою очередь, должны быть представлены как проявления наиболее фундаментальных законов протекающих в живых организмах биологических процессов.
Последующее развитие структурно-функционального направления в изучении клетки в полной мере выявило, с одной стороны, огромные возможности современной науки проникать вглубь структурной организации клетки, а с другой стороны, принципиальную ограниченность данного направления в познании интегративных свойств клетки как наиболее фундаментального элемента более сложных многоклеточных живых организмов.
Признавая большую познавательную ценность данного направления в изучении живой клетки, мы тем не менее считаем, что при построении математической теории клетки и внутриклеточных процессов значительно более перспективным являлось второе - феноменологическое - направление, которое отвлекается от материальной структуры клетки и от конкретных физико-химических механизмов взаимодействия отдельных элементов внутриклеточной организации и рассматривает клетку как целостную систему взаимосвязанных процессов, описываемых через функциональные зависимости, существующие между различными параметрами клетки и внутриклеточной среды. Достаточно очевидно, что это направление может развиваться лишь на основе обобщения и постоянного учета полученных конкретно-эмпирическими методами исследования фактических данных о строении клетки и о протекающих в ней процессах. Однако при феноменологическом описании эти данные учитываются не непосредственно, а в "снятом", так сказать, виде, через математическую формулировку (математический вид) функциональных зависимостей между биохимическими, биофизическими и физиологическими параметрами клетки, а также через ограничения, накладываемые на пределы допустимых изменений тех или иных параметров, характеризующих условия, в которых протекают описываемые процессы. В конечном итоге данное направление должно привести к установлению специфически биологических законов, которым подчиняются внутриклеточные материальные процессы, и к формированию таких феноменологических теорий, которые будут способны количественно описывать течение внутриклеточных процессов, а в дальнейшем и функционирование клетки как целостной системы.
В развитии физики, отмечает В. Гейзенберг, феноменологические теории всегда играли значительную роль, причем они “развиваются всегда там, где наблюдаемые явления еще не могут быть сведены к общим законам природы. Причина этой невозможности может состоять либо в чрезвычайной сложности соответствующих явлений, которая еще не допускает такое сведение из-за математических трудностей, либо в незнании упомянутых законов” /Гейзенберг, 1967, с.731/. Еще более важная причина частого обращения в физике к феноменологическим теориям заключается в том, что материальными носителями действующих в неживой природу "сил", а также материальными субстратами эмпирически наблюдаемых явлений и процессов оказываются объекты и процессы микромира, труднодоступные для экспериментального изучения.
Совершенно иначе обстоит дело в биологии. Здесь "материальные механизмы" процессов жизнедеятельности живого организма оказались "слишком доступными" для непосредственного наблюдения. Более того, доступными для непосредственного экспериментального изучения оказались материальные носители не только собственно биологических, но и многих лежащих в их основе физических и химических процессов. Отсюда велик соблазн искать "механизмы" биологических процессов в области химических реакций и физических взаимодействий на уровне молекул, атомов и даже элементарных частиц, "из которых состоят биологические системы" и которые "лежат в основе биологических процессов". Поэтому для построения "феноменологических" теорий биологических систем и процессов необходимо, во-первых, правильно определить тот предельно низкий уровень структурной организации живой клетки, с которого начинается собственно "живая материя", а во-вторых, осознанно абстрагироваться (отвлечься) от материальной структуры живых организмов и сосредоточить все внимание на "внешней" стороне именно биологических явлений, т.е. на тех закономерностях, в соответствии с которыми эти явления организованы в пространстве и во времени. Именно о том, насколько трудно современным исследователям абстрагироваться от физических, химических и физико-химических "механизмов" биологических процессов живого организма, свидетельствуют результаты тех дискуссий о путях построения теоретической биологии, которые состоялись в 70-80 годы.
В ходе этих дискуссий выяснилось, что исследователи вкладывали весьма разное содержание в понятие "теоретическая биология" и по-разному понимали смысл теоретических обобщений эмпирических фактов биологии.
Суть дискуссий свелась, фактически, к проблеме правомерности редукции биологии к физике. Однако исследователи, отстаивавшие противоположные точки зрения, находились не в равных условиях, поскольку ученые, считавшие, что теоретическая биология должна строиться на каких-то собственных исходных принципах, еще не могли сформулировать эти принципы. Их позиция в основном опиралась на весьма зыбкие интуитивные представления и догадки самого общего характера, тогда как на вооружении сторонников сведения биологических процессов к лежащим в их основе физическим и химическим процессам, были вся мощь и весь опыт теоретической физики в математическом описании многообразных процессов и явлений физического мира. Веским аргументом при этом представлялось то обстоятельство, что в живой клетке "содержатся те же элементы периодической системы, что и в объектах неживой природы. Никаких химических элементов, присущих только живому, не существует" /Блюменфельд, 1977, с.14/. Отсюда казалось логичным делать вывод о том, что любые взаимодействия составных элементов клетки и любые протекающие в живых клетках процессы реализуются через те же физические поля, через которые эти химические элементы взаимодействуют, вступая в химические реакции, и порождают все многообразие материальных процессов в живой природе.
Возобладанию такой точки зрения весьма способствовало и то обстоятельство, что выдвигавшаяся Э.С. Бауэром, Э. Шредингером и некоторыми другими биологами в качестве специфической особенности живых организмов и даже как “всеобщий закон биологии” (Э.С. Бауэр) способность биологических систем “поддерживать себя на постоянном и достаточно низком уровне энтропии” благодаря тому, что “организму удается освобождаться от всей той энтропии, которую он вынужден производить, пока жив” /Шредингер, 1972/, оказалась в определенной степени присущей и открытым системам неживой природы. Как показал И. Пригожин, находящиеся в существенно неравновесных состояниях открытые системы неживой природы способны к самоорганизации, т.е. к образованию упорядоченных структур, названных им диссипативными /Пригожин, 1960; 1964; 1985; 1990; Николис, Пригожин, 1979, 1990/.
В настоящее время термодинамическая теория диссипативных структур и неравновесных состояний открытых систем многими исследователями рассматривается как надежная основа построения феноменологических теорий биологических систем и процессов. Однако способность живых организмов поддерживать и даже повышать уровень своей организации не возникла из ничего, а явилась результатом развития аналогичных свойств некоторых открытых систем неживой природы. Но в процессе формирования и развития живой материи это свойство открытых систем неживой природы поднялось на качественно новый уровень, и если открытые системы неживой природы для поддержания и повышения уровня своей организации нуждаются в постоянном притоке энергии извне, то живые организмы поддерживают и повышают уровень своей организации за счет внутренней энергии. Поэтому теория диссипативных структур описывает те свойства открытых систем неживой природы, на основе развития которых появилась способность живых организмов за счет своей внутренней энергии поддерживать и развивать уровень своей организации. Термодинамика неравновесных процессов открытых систем и теория диссипативных структур в лучшем случае способны описать самые ранние стадии формирования и развития таких предбиологических систем неживой природы, дальнейшее развитие которых привело к возникновению живых организмов. Этим объясняется, на наш взгляд, проявившаяся в процессе развития современной биофизики ограниченная возможность использования теории диссипативных структур для описания и объяснения биологических систем и процессов.
В отличие от биофизиков, отстаивавших достаточность известных законов физики для описания и понимания биологических систем и процессов, позиция противников редукции биологии к физике была осложнена тем обстоятельством, что обосновать её можно было только создав качественно новую теоретическую биологию.
Поэтому не удивительно, что к концу 70-х годов господствующее положение в сознании большинства исследователей заняла концепция достаточности известных законов физики для описания биологических систем и процессов. На сегодняшний день эта позиция получила развернутую реализацию в современной биофизике. Однако современные достижения биофизики далеко не соответствуют тем надеждам, которые возлагали на теоретическую биологию исследователи в середине ХХ столетия
.Итак, сложность построения в биологии таких феноменологических теорий, которые адекватно отражали бы специфику живой материи, заключается в трудности абстрагирования от доступных непосредственному наблюдению молекулярных "механизмов" наиболее фундаментальных биологических процессов, а следовательно, и от тех физических и физико-химических теорий, которые позволяют математически описывать функционирование этих "механизмов". Ситуация усугубляется еще и тем, что господствующая в экспериментальной биологии редукционистская установка не позволяет уделять должное внимание поискам собственно биологических, не подчиняющихся физическим и физико-химическим законам принципов организации биологических процессов. Более того, на наш взгляд, именно редукционистский способ мышления помешал исследователям, занятым проблемами теоретического описания биологических процессов, должным образом оценить выдающееся по своей сути эмпирическое открытие рядом биологов биологического времени.
Правильному восприятию результатов исследований таких ученых, как Т.А. Детлаф , Г.П. Еремеев, Г. Кейт, Д.А. Сабинин, К. Торнтвейт, Х. Фрай, и др., мешало и то обстоятельство, что признание используемых ими единиц длительности единицами особой формы времени вступало в резкое противоречие с общепринятыми представлениями, согласно которым время - это нечто единое, универсальное, всеобщее, равномерно текущее и достаточно точно измеряемое общепринятыми единицами при помощи обычных часов. Вполне естественно, что, не имея достаточно обоснованного положительного решения философской проблемы многообразия типов времени, трудно отойти от господствующих в сознании людей понятий и признать биологическое время столь же полноценным, каким признается физическое время.
Но, как мы показали, принятые ныне представления о времени нуждаются в серьезном пересмотре. Мнение об уникальности времени и о принципиальной невозможности его измерения не иначе, как обычными часами и общепринятыми единицами, основано на негласном признании единственности класса равномерных и строго периодических процессов. Анализ же свойств равномерности и периодичности материальных процессов показал, что они являются не абсолютными, а соотносительными свойствами и что в принципе возможно существование неограниченного множества соравномерных (и периодических эквивалентных) процессов.
В предыдущей главе был рассмотрен класс инерциально-равномерных движений, от которых абстрагировано общепринятое представление о времени, и было показано, что соравномерность входящих в этот класс механических движений возникает благодаря подчиненности соответствующих динамических систем закону сохранения механической энергии. Но
соравномерность материальных процессов может быть обусловлена и другими причинами, например, принадлежностью их целостной высокоинтегрированной материальной системе. Примерами таких систем являются живые организмы.О том, что в живых организмах существуют классы соравномерных процессов, синхронно и пропорционально ускоряющих и замедляющих свой ход под воздействием множества различных и, в том числе, случайным образом изменяющихся факторов, свидетельствуют результаты исследований Т.А. Детлаф и ее коллег. Они установили, что с изменением температуры среды длительности различных этапов эмбрионального развития пойкилотермных животных изменяются пропорционально и что эта закономерность имеет фундаментальный характер, охватывая процессы всех структурных уровней организации эмбриона. Как пишет Т.А. Детлаф, “... с изменением температуры пропорционально изменяется длительность процессов, имеющих самую разную природу и осуществляющихся на разных уровнях организации организма: внутриклеточном (молекулярном и ультраструктурном), клеточном (при делении клеток и их дифференцировке), на уровне морфогенетических движений, процессов индукции и органогенеза” /Детлаф, 1996, с. 140/. Иными словами, вся совокупность биологических процессов, из которых складывается развитие эмбриона, ведет себя как единый целостный поток, синхронно и пропорционально изменяя свою скорость в зависимости от изменений температуры среды. В этом едином потоке имеются как сравнительно медленные (например, протекающие на клеточном уровне процессы деления клеток и их дифференцировка), так и весьма быстрые, протекающие на внутриклеточном, молекулярном уровне, к которым относятся, например, ферментативные реакции внутриклеточного метаболизма. При этом достаточно очевидно, что если бы на каких-то структурных уровнях организации эмбриона нарушалась синхронность и пропорциональность изменения темпов биологических процессов, то это разрушило бы закономерное течение всего потока процессов формирования и развития живого организма. Подчеркивая это обстоятельство, Т.А. Детлаф пишет: “Не будет преувеличением, если мы скажем, что без этой способности пойкилотермные организмы вообще не могли бы существовать в меняющихся условиях внешней среды: если бы разные компоненты комплекса процессов, из которых складывается любой этап развития, изменялись асинхронно, то это приводило бы к возникновению нарушений нормального развития, а на более поздних стадиях - к нарушению нормального функционирования организма. Не случайно, что одной из первых реакций зародышей на приближение к границам оптимальных температур является десинхронизация отдельных процессов развития” /Там же/.
Пропорциональность изменений длительностей различных процессов эмбрионального развития пойкилотермных животных при изменениях температуры внешней среды позволяет, взяв за единицу длительность одного из этапов эмбрионального развития, выразить через нее длительности всех остальных этапов. В качестве такой единицы в лаборатории Т.А. Детлаф избрана длительность одного митотического цикла периода синхронных делений дробления (t
Такой способ перевода минут в “ детлафы” может создать ложное представление о том, что измеряемое при помощи детлафов биологическое время - это аффинно преобразованное физическое время. В действительности же биологическое время взаимно стохастично с физическим и не может быть результатом аффинного преобразования физического времени. Но для того, чтобы выявить взаимную стохастичность биологического и физического времени, необходимо от измеряемой детлафами макроструктуры биологического времени перейти к измеряемой значительно более мелкими единицами его “ тонкой структуре” . Возможность перехода от детлафов к более мелким единицам измерения длительности обеспечена тем, что синхронность и пропорциональность изменений длительностей биологических процессов представляют собой фундаментальное свойство живой материи и охватывают процессы всех уровней ее организации. Поэтому если в некотором интервале длительности содержится Р
При переходе от одного масштаба биологического времени к другому мы увидим , что если на уровне медленных, измеряемых “ детлафами” процессов температуру среды можно рассматривать как изменяющуюся медленно и плавно, а на протяжении отдельных этапов эмбрионального развития считать и вовсе постоянной, то на уровне быстрых внутриклеточных процессов мы не можем игнорировать быстрые стохастические колебания температуры. Поэтому определяемые быстрыми внутриклеточными процессами мелкие единицы биологического времени обретают характер стохастической переменной величины по отношению к равномерному физическому времени. Иными словами, в своей “ тонкой структуре” биологическое время оказывается взаимно стохастичным с физическим временем, а следовательно, при достаточно точном измерении оно стохастично с физическим временем и на более высоких уровнях. Но если коэффициент С достаточно велик и, следовательно, крупные единицы биологического времени состоят из большого числа мелких единиц, то случайные колебания последних, усредняясь, весьма слабо скажутся на величинах крупных единиц.
Взаимная стохастичность биологического и физического времени на уровне их “ тонкой структуры” говорит о том, что при хронометрировании протекающих в живом организме материальных процессов в единицах биологического времени единицы физического времени становятся последовательностью случайных величин. Но справедливо и обратное: если хронометрировать биологические процессы в единицах физического времени, то все процессы, которые в биологическом времени подчиняются динамическим законам, предстанут как стохастические процессы
.Вполне естественно предположить, что при таком характере взаимосвязи биологического и физического времени биологические процессы в живом организме начинаются только с определенного уровня организации его материального субстрата и, соответственно, на этом уровне возникает биологическое время. Имеются определенные основания считать, что таким фундаментальным уровнем структурной организации живой материи и протекающих в ней биологических процессов является уровень ферментативных реакций внутриклеточного метаболизма.
Приступая к обсуждению этого вопроса, мы прежде всего должны отметить, что во временной структуре внутриклеточных процессов ферментативные реакции метаболизма относятся к наиболее быстрым процессам. На это обстоятельство обратил свое внимание в 60-х годах Б. Гудвин в весьма интересной, с точки зрения обсуждаемой нами проблемы, книге “Временная организация клетки” /Гудвин, 1966/.
Опираясь на разработанную в современной физике идею разделения нестационарных процессов на качественно различные ступени, относящиеся в соответствии с их временами релаксации к разным масштабам времени, Б.
Гудвин, вслед за Уоддингтоном, делит внутриклеточные процессы на следующие три группы: 1/ Быстрые биохимические процессы, включающие транспорт и химические превращения "малых" молекул ("метаболическая система"); 2/ обладающие средними скоростями процессы биосинтеза, диффузии и взаимодействия макромолекул ("эпигенетическая система") и 3/ совокупность медленных генетических изменений биологических систем ("генетическая система").В своей работе Б. Гудвин отвлекается как от слишком медленных генетических изменений параметров клетки, так и от слишком быстрых процессов метаболической системы и ставит перед собой задачу смоделировать процессы, относящиеся к эпигенетической системе клетки. Исходя из того факта, что времена релаксации процессов метаболической и эпигенетической систем клетки лежат соответственно в пределах
Однако процессы эпигенетической системы невозможно рассматривать как абсолютно не зависящие от биохимических реакций метаболической системы и поэтому их приходится рассматривать "погруженными" в "шумящее", т.е. подверженное случайным колебаниям, "биохимическое пространство" метаболической системы клетки. Но поскольку это "пространство" не определено однозначно, то, как пишет автор, “траектории детерминированных осцилляторов ("эпигенетической системы". - И.Х) перестают быть строго детерминированными. Поэтому приходится говорить только об усредненных траекториях, и все динамические свойства управляющих систем (клетки. - И.Х.) должны описываться с вероятностных позиций” /Гудвин, 1966, с.100-101
/.Таким образом, в результате воздействия на осцилляторы эпигенетической системы случайных колебаний процессов метаболической системы эпигенетическая система оказывается набором стохастических осцилляторов, а поскольку входящие в эпигенетическую систему процессы биосинтеза, диффузии и взаимодействия макромолекул лежат в основе регуляторных механизмов клетки, то и вся клетка предстает как совокупность почти не связанных между собой и подчиняющихся вероятностным законам биохимических осцилляторов. Однако подобное уподобление клетки газу не отражает природы живой материи, и мы вполне согласны с А.М. Молчановым, который, отмечая, что при математическом описании клетки пока приходится выбирать между двумя крайними подходами, из которых один уподобляет клетку механизму, другой - газу, писал: « При всей грубости и жесткости первого подхода он неизмеримо ближе к истине, чем второй, так как исходит из главного - высокой степени эволюционной зрелости такого замечательного и сложно организованного биологического объекта, как клетка” /Молчанов А.М., 1967, с.308/.
Одной из наиболее важных причин неудачи Б. Гудвина в моделировании временной структуры внутриклеточных процессов, на наш взгляд, явилось игнорирование им быстрых биохимических реакций внутриклеточного метаболизма. Он полагал, что при математическом описании клетки можно усреднять параметры, зависящие от наиболее быстрых метаболических процессов, и в основу математической модели клетки можно положить уравнения, описывающие сравнительно медленные процессы эпигенетической системы. Подобный путь к описанию клетки представляет собой своего рода "макроскопический" (во временном отношении) подход к биологическим процессам. При этом он исходил из предположения, что “...для адекватного описания феноменологических свойств макроскопической системы вовсе не обязательно использовать микроскопический подход” /Гудвин, 1966, с.101/. Однако он упустил из виду, что при макроскопическом подходе к описанию материальных систем и процессов легко могут ускользнуть из поля зрения нарушающие какую-либо важную симметрию мира и тем самым качественно изменяющие реальную действительность бесконечно малые (с точки зрения макроскопического уровня) возмущения описываемой системы
.Именно с такого рода ситуацией мы и сталкиваемся при попытках усреднять параметры метаболической системы клетки и описывать протекающие в клетке процессы в единицах физического времени. При этом нарушается самоконгруэнтность единиц биологического времени и стохастичность единиц физического времени относительно биологического оборачивается стохастичностью биологических процессов относительно физического времени.
О недопустимости отношения к метаболическим процессам как к некоторому "биохимическому фону", на котором разыгрываются сравнительно медленные "собственно биологические" процессы эпигенетической системы, говорят и многочисленные факты, свидетельствующие о том, что относящиеся к метаболической системе клетки ферментативные реакции внутриклеточного обмена веществ составляют содержание, "живую ткань" собственно биологических процессов.
В пользу предположения о том, что наиболее фундаментальные единицы биологического времени следует искать среди периодов циклических метаболических процессов клетки, можно привести и следующий аргумент.
Рассмотренные нами работы биологов, использующих специфические единицы измерения длительности, и в особенности работы Т.А. Детлаф и ее коллег, на наш взгляд, убедительно доказывают, что биологические процессы живых организмов объективно структурированы в особом биологическом времени. Но тогда логично предположить, что временные характеристики генетической информации также должны быть закодированы в единицах биологического времени. Для того чтобы это могло быть выполнено, во-первых, должны существовать естественные единицы (“ кванты” ) времени и, во-вторых, они должны быть связаны с такими процессами, которые позволяют вести непрерывный их счет с момента оплодотворения яйцеклетки и до гибели живого организма. Такими “ сквозными” для всех этапов развития организма биологическими процессами, видимо, являются лишь ферментативные реакции внутриклеточного метаболизма.
Центральными двигателями метаболического процесса, своеобразными “ машинами метаболизма” являются молекулы фермента, представляющие собой гигантские макромолекулы, имеющие весьма сложную структуру.
Как известно, ферменты - это сложные белковые вещества, молекулы которых состоят примерно из 20 типов аминокислотных остатков, соединенных между собой ковалентными (пептидными) связями в длинные полипептидные цепочки. Молекулы фермента могут состоять из одной или нескольких полипептидных цепочек, уложенных благодаря различного рода внутримолекулярным взаимодействиям в сложную пространственную структуру, в которой обычно выделяют несколько уровней.
Геометрия пептидных связей такова, что между аминокислотными остатками, отстоящими друг от друга по крайней мере на один аминокислотный остаток, могут устанавливаться водородные связи. Если при этом реализуются все возможные связи, то линейная полипептидная цепь образует некоторую периодическую спиралевидную структуру (альфа-спираль). В молекулах белка, состоящих из нескольких полипептидных цепочек, водородные связи могут соединять пептидные группы соседних цепей, образуя так называемую бета-форму полипептида. Подобного рода поперечные водородные связи могут устанавливаться и между соседними участками одной и той же полипептидной цепи, образуя "гармошку" кросс бета-форму. В свою очередь, закрученные в "спираль" или уложенные "лесенкой" или "гармошкой" полипептидные цепочки белковых молекул, благодаря водородным, дипольдипольным, индукционным и другим внутримолекулярным связям стягиваются в более сложные пространственные структуры и макромолекулы белка принимают таким образом достаточно компактные глобулярные формы. При этом от однозначно определяемой генетической информацией конфигурации молекул фермента, т.е. последовательности аминокислотных остатков в ее полипептидной цепи (или цепях) пространственная структура макромолекулы или, иначе, ее конформация, может претерпевать обратимые изменения.
На протяжении длительного времени предполагалось, что конформационные изменения макромолекул белка представляют собой результат каких-либо определенных воздействий на фермент извне (например, слабого нагревания, взаимодействия с теми или иными метаболитами, ионами металлов и т.д. (См., например: /Кретович,1967/). Но открытые в конце 50-х годов С.Э. Шнолем /Шноль, 1958/ и затем подробно изученные им и его сотрудниками самопроизвольные циклические изменения многих показателей растворов актина, миозина и актомиозина свидетельствуют о том, что белковая молекула по самой своей природе является динамичной, постоянно и самопроизвольно изменяющей свою пространственную структуру системой. В дальнейшем на основе значительных серий опытов с большим числом различных препаратов было показано, что самопроизвольные конформационные колебания являются свойством всех белков /Шноль и др., 1980/.
Для объяснения механизмов ферментативного катализа большой интерес представляют, на наш взгляд, высказываемые некоторыми авторами мысли о том, что молекула фермента участвует в катализируемой ею реакции “не только как штатив, закрепляющий детали механизма, но и как двигатель в этом механизме” /Шноль, 1967, с. 27/.
Мнение о том, что молекула фермента представляет собой своего рода "энергетическую машину" /Робертис и др., 1967, с.59/, которая при наличии некоторого источника энергии способна совершать определенную работу по перестройке химической структуры молекул субстрата катализируемой ею реакции, по нашему мнению, более адекватно отражает природу биологических катализаторов, чем отождествление их с обычными химическими катализаторами.
В настоящее время можно считать доказанным, что каждый элементарный акт ферментативного катализа представляет собой многоступенчатый циклический процесс, в ходе которого молекула фермента соединяется с молекулой (или молекулами) субстрата и образуется так называемый фермент-субстратный комплекс, который, претерпев ряд последовательных изменений, распадается на свободный фермент и конечный продукт (или продукты) реакции, и может начаться новый цикл каталитического процесса.
Поскольку при этом предполагается, что в макроскопическом объеме реагирующей среды единичные акты ферментативного катализа распределены в пространстве и во времени случайным образом, то усреднение во времени протекающих в реагирующей среде химических превращений позволяет отдельные стадии ферментативного катализа рассматривать как самостоятельные химические реакции, связанные между собой через участвующие в каталитическом процессе реагенты и промежуточные соединения.
В основе теории химических реакций лежит введенное Эйрингом /Eyring, 1935/ представление о том, что, прежде чем претерпеть химическое изменение, молекулы субстрата проходят через переходное, так называемое, активированное состояние с максимальной энергией. Поскольку время жизни субстратов и продуктов реакции много больше времени существования активированного комплекса, то каждый элементарный акт химической реакции рассматривается как мгновенное событие. При этом предполагается, что в макроскопических объемах реагирующей среды, где совершается большое число элементарных химических превращений, происходит усреднение во времени мгновенных "скачков", и химическая реакция может рассматриваться как непрерывный процесс.
Аналогичные представления о непрерывности протекающих в макроскопических объемах реагирующей среды химических превращений используются и в теории ферментативного катализа. Однако еще в начале 60-х годов серьезные возражения против подобных представлений высказал Христиансен /Christiansen, 1960/.
Предположим, пишет Христиансен, реакция
В![]() + В
+ В![]() + В
+ В![]() = А
= А![]() + А
+ А![]() + А
+ А![]() , / В /
, / В /
имеющая положительное направление слева направо, катализируется ферментом в три ступени
В
В![]() + Х
+ Х![]() = Х
= Х![]() + А
+ А![]() / 2 / / А /
/ 2 / / А /
В![]() + Х
+ Х![]() = Х
= Х![]() + А
+ А![]() , / 3 /
, / 3 /
где
Формула
Предположим далее, что мы наблюдаем реакцию в момент, когда
Переходя к рассмотрению случая, когда в элементе объема содержится большое число молекул фермента, Христиансен пишет: “Можем ли мы предполагать, что различные молекулы находятся одновременно в одном и том же состоянии? Или, выражаясь иными словами, является ли мгновенное распределение ферментов по различным состояниям одинаковым по всей реагирующей среде?
Согласно термодинамике, ясно, что ответ на поставленный вопрос должен быть утвердительным, поскольку мы знаем, что для того, чтобы перевести всю систему из состояния, в котором распределение по всей системе одинаково, в состояние с разным распределением, требуется затрата работы. Поэтому первое состояние более вероятно, чем второе, и, как обычно в статистической термодинамике, настолько, что практически оно одно и возможно. Мы можем поэтому считать, что циклические трансформации отдельных молекул фермента должны всегда происходить в фазе или что система должна быть когерентна в отношении превращений фермента” /Там же, с.108/.
К выводам, аналогичным тем, к которым пришел Христиансен, можно прийти и в том случае, если качественно проанализировать совокупность физических и физико-химических процессов, составляющих ферментативный каталитический цикл.
Представим себе, что в некотором ограниченном объеме внутриклеточной среды, состоящей в основном из молекул воды и растворенных в ней, как правило, небольших молекул реагентов (субстратов и продуктов), а также некоторых других веществ, протекает катализируемая молекулами фермента биохимическая реакция.
В этой среде резко выделяются гигантские макромолекулы фермента, состоящие из многих сотен атомов и имеющие сложную пространственную структуру. Они представляют собой осцилляторы, в которых колебания происходят как на уровне элементарных частиц и атомных ядер, так и на уровне достаточно крупных групп атомов. Среди огромного числа колебательных систем всегда найдутся осцилляторы, способные воспринять кинетическую энергию соударяющихся с макромолекулой фермента молекул среды, молекулярные веса которых, как правило, сравнимы с молекулярными весами внутримолекулярных осцилляторов. Если при этом учесть, что момент инерции центра массы макромолекулы велик и что соударения молекул среды с молекулой фермента распределены по поверхности последней случайным образом, то можно сделать вывод, что воспринимаемая макромолекулой внутренняя (молекулярно-кинетическая) энергия окружающей среды будет в основном идти на возбуждение ее колебательных систем, а не на возбуждение броуновского движения ее центра масс.
Поскольку между колебательными системами макромолекулы существуют различного типа связи, то воспринятая теми или иными осцилляторами внутренняя энергия окружающей среды будет передаваться вдоль некоторых связей другим осцилляторам, и в молекуле фермента возникнут потоки колебательной энергии.
В силу того, что связи, вдоль которых может передаваться колебательная энергия, должны удовлетворять определенным условиям /Мандельштам, 1955/, то при каждой конформации в макромолекуле будут существовать вполне определенные пути миграции колебательной энергии. Миграция колебательной энергии может быть причиной конформационных изменений макромолекулы, поскольку при некоторых распределениях энергии в ней могут временно разрываться (или, по крайней мере, ослабляться) те или иные внутримолекулярные связи, что может нарушать устойчивость конформации, а при некоторых дополнительных условиях, например, при достижении суммарной колебательной энергии определенных критических значений, и к переходу макромолекулы в иную конформацию.Если учесть, что в общем случае внутримолекулярные связи ограничивают число колебательных степеней свободы внутримолекулярных осцилляторов, то разные конформации макромолекулы фермента, обладая, как правило, разным числом внутримолекулярных связей, характеризуются и разным числом колебательных степеней свободы, а следовательно, разной степенью энергетической емкости. Однако переход от конформации с меньшим числом внутримолекулярных связей к конформации с большим их числом должен сопровождаться уменьшением накопленной в макромолекуле колебательной и конформационной энергии, поэтому такой переход требует для погашения "избыточной" энергии каких-то "точек приложения". Подобной "точкой приложения" может служить перестраиваемая при ферментативной реакции химическая структура молекулы (или молекул) субстрата катализируемой ферментом реакции.
В силу большой частоты соударений молекул среды с макромолекулой фермента, мы можем считать, что преобразуемая в колебательную энергию внутримолекулярных осцилляторов внутренняя энергия окружающей среды "втекает" в макромолекулу в виде непрерывного потока. Но поскольку тепловое движение молекул среды подвержено флуктуациям, то интенсивность потока энергии будет также флуктуирующей величиной. Поэтому длительность пребывания макромолекулы фермента в состоянии устойчивой конформации будет случайной величиной.
Рассматривая среду, в которой протекает катализируемая растворенными в ней молекулами фермента биохимическая реакция, С.Э. Шноль пишет:: “Представим себе... большое число... макромолекул фермента в растворе, содержащем соответствующий субстрат. По существу речь здесь идет о множестве генераторов механических колебаний, распределенных в среде, в которой они совершают циклические изменения конформации. Поскольку эти генераторы полностью идентичны, обязательно должно происходить их взаимодействие, приводящее к образованию упорядоченных в пространстве синхронно колеблющихся ассоциаций ферментных макромолекул. В результате в растворе должны образоваться структуры типа жидких кристаллов, отличающихся от обычных своей эфемерностью - они представляют собой ансамбли лишь работающих макромолекул фермента” /Шноль, 1979, с. 74/.
С.Э. Шноль рассматривает здесь ферментативный процесс в динамике, а мы для уяснения некоторых особенностей этого процесса остановим его и рассмотрим поэтапно.
Представим себе, что макромолекулы фермента, находящиеся в одной из своих устойчивых конформаций, образуют описанную выше кристаллическую структуру. Поскольку каждая молекула фермента состоит из огромного числа в общем случае электрически заряженных и совершающих колебательные движения групп атомов, то вокруг каждой ферментной молекулы должны существовать сложные электростатические и электромагнитные поля. А если учесть, что молекулы воды представляют собой диполи, определенным образом ориентирующиеся в электростатических полях, возникающих вокруг и между макромолекул фермента, то можно предположить, что на тех этапах каталитического цикла, когда молекулы фермента находятся в своих устойчивых конформациях, жидкокристаллическую структуру обретает и окружающая молекулы фермента водная среда. В такой среде будут существенно нарушены многие действующие в обычной жидкости гидродинамические законы, в частности, предельно снижена скорость диффузии веществ.
Однако картина резко меняется в моменты скачкообразных переходов макромолекул от одной конформации к другой, поскольку при этом резко перестраивается структура электростатических и электромагнитных полей, а часть освобождаемой конформационной энергии рассеивается в окружающую среду, разрушая ее кристаллическую структуру и усиливая тепловое движение молекул среды. Эти короткие "мгновения" конформационных переходов предельно малы по сравнению с длительностью периодов существования устойчивых конформаций. Тем не менее они имеют определенную временную длительность, на протяжении которой восстанавливается "нормальное" действие гидродинамических законов, а скорость диффузии различных веществ в результате интенсивного перемешивания среды значительно возрастает. Но как только макромолекула фермента примет новую устойчивую конформацию и стабилизируются окружающие ее физические поля, реагирующая среда примет новую кристаллическую структуру и снова обретет жидкокристаллические свойства
.Таким образом, имеются определенные основания предположить когерентность каталитических циклов молекул фермента, катализирующих в клетке данную биохимическую реакцию
.Рассмотрим теперь более подробно временную структуру каталитических циклов.
Обозначим длительность
При таких обозначениях полную длительность
![]()
Поскольку второй член много меньше первого и с большой степенью точности во всех каталитических циклах сохраняется постоянным, то полный период каталитического цикла будет зависеть в основном от длительностей существования устойчивых конформаций фермента и фермент-субстратного комплекса, т.е. от величины первого члена этой суммы. Но как мы отметили выше, длительность существования устойчивой конформации фермента зависит от постоянно флуктуирующей интенсивности "втекающего" в макромолекулу фермента потока тепловой энергии окружающей среды. Поэтому длительности существования фермента в данной устойчивой конформации в разных каталитических циклах, т.е.
Однако каждый каталитический цикл данной ферментативной реакции, независимо от выраженной в единицах физического времени длительности цикла, вносит в реагирующую среду вполне определенные изменения, которые для серии следующих друг за другом каталитических циклов будут оставаться неизменными.
Действительно, каждая участвующая в каталитическом процессе молекула фермента за один каталитический цикл расходует определенное количество молекул субстрата, производит определенное количество молекул продукта катализируемой реакции, а также расходует или выделяет (в зависимости от энергетических характеристик реакции) определенное количество энергии. При этом каталитические циклы состоят из одинаковых последовательностей конформационных переходов ферментных молекул, в ходе которых реагирующая среда претерпевает вполне определенную последовательность как циклических,
так и однонаправленных необратимых изменений. Так, на протяжении каждого каталитического цикла в определенной последовательности появляются и исчезают различные конформации фермента и фермент-субстратного комплекса; резко меняются свойства реагирующей среды в периоды скачкообразных переходов макромолекул фермента от одной устойчивой конформации к другой; причем независимо от того, идет ли реакция в целом с поглощением или выделением энергии, при конформационных переходах некоторая часть энергии молекулы фермента рассеивается в реагирующую среду и расходуется на разрушение ее кристаллической структуры. И, наконец, резкие изменения пространственной конфигурации макромолекулы должно вести к резким скачкам амплитуд электромагнитных излучений его электрически заряженных осцилляторов.Общая длительность каталитического цикла зависит в основном от продолжительности существования стабильных конформаций (т.е. от величин
Что касается количества участвующих в реагирующей среде макромолекул фермента, то оно не подвержено случайным колебаниям, а целенаправленно регулируется при помощи различных модификаторов (активаторов и ингибиторов) и поэтому может быть представлено как функция некоторых параметров.
На основе изложенного можно предположить, что биологически значимая длительность бытия живой клетки определяется не количеством единиц физического времени, а количеством каталитических циклов каких-то ведущих ферментативных реакций внутриклеточного метаболизма или, возможно, более сложных многоступенчатых циклических ферментативных процессов (типа цикла Кребса).
Следует особо заметить, что в интервалах длительности, меньших, чем полные периоды каталитических циклов, в реагирующей среде еще нет биологических процессов, а протекают физические и физико-химические процессы, которые, благодаря специфической организации реагирующей среды и специфическим свойствам молекул фермента, на протяжении каталитического цикла интегрируются в элементарные акты биохимической реакции и связанных с ними биофизических и физиологических процессов. Вместе с тем было бы ошибочным предполагать, что математически развитую теорию элементарных актов биологических процессов можно будет построить на основе физических и физико-химических теорий тех процессов, из которых состоит каталитический цикл ферментативной реакции, поскольку для этого, во-первых, пришлось бы объединять в единую синтетическую теорию качественно разные физические теории, описывающие поведение реагирующей среды в жидком и жидкокристаллическом состояниях, и, во-вторых, учесть стохастичность величин
Таким образом, биологическое время представляет собой не континуальное, а дискретное квантованное время, неделимыми квантами которого являются полные периоды каталитических циклов каких-то ведущих ферментативных реакций внутриклеточного метаболизма.
Квантованность биологического времени обусловлена, на наш взгляд, и тем обстоятельством, что реализация генетической информации требует достаточно жесткого контроля со стороны генетического аппарата клетки за временными характеристиками процессов становления и развития живого организма. Если при этом допустить, что в генетическом аппарате клетки ведется счет квантам биологического времени, то каждая клетка многоклеточного живого организма, ведя свое происхождение от одной единственной яйцеклетки, “может знать” на каждый данный момент времени количество прожитых организмом “квантов” биологического времени и с учетом этого реализовывать дальнейшие фрагменты генетической информации. Правда, для подобной согласованности во времени деятельности генетических аппаратов всех клеток живого организма необходима синхронизация во всех клетках каталитических циклов ферментативных реакций, которые задают кванты биологического времени, что, на первый взгляд, представляется совершенно невероятным. Но такое предположение оказывается вполне допустимым, если учесть открытое С.Э. Шнолем и на протяжении нескольких десятилетий изучаемые им и его коллегами явление синхронизации макроскопических флуктуаций колебательных процессов различной природы
.В 1956 г. С.Э. Шноль, работая с препаратами мышечных белков, обратил внимание на необычно большой разброс результатов измерений АТФ-азной активности фермента миозина. Изучение всевозможных источников ошибок: недостаточности перемешивания, негомогенности растворов, непостоянства температуры, нестабильности измерительных приборов и т.д., - привело С.Э. Шноля к выводу, что причиной наблюдаемого разброса измеряемых величин является колебательный характер протекающих в растворах белка процессов. Это заставило С.Э. Шноля и других исследователей, заинтересовавшихся этим явлением, обратиться к исследованию колебательных процессов в биохимических системах. Первые результаты были обсуждены на 1 Всесоюзном симпозиуме по колебательным процессам в химических и биологических системах в 1966 году в Пущино
.Уже к этому времени С.Э. Шноль и его коллеги пришли к выводу, что наблюдаемый ими "разброс результатов" не является следствием каких-либо кинетических колебательных процессов и что речь идет скорее не о колебаниях, а о флуктуациях, которые
могут охватывать макроскопические объемы и происходить одновременно в разных частях сосудов с растворами белка /Шноль, 1965/. “Поскольку при наблюдавшихся флуктуациях изменялась не только ферментативная активность, но и число титрируемых SН-групп, было предположено, что "макроскопические флуктуации" являются следствием синхронных изменений конформации макромолекул белков” /Удальцова и др., 1987, с.4-5/. При этом предполагалось, что синхронизация конформационных колебаний молекул фермента во всем объеме раствора является следствием взаимодействия макромолекул через разделяющую их среду /Шноль, 1969/.Исходя из этих представлений, С.Э. Шноль и его сотрудники долгое время рассматривали обсуждаемый феномен как "конформационные колебания" макромолекул белка и изучали зависимость амплитуды этих колебаний как от свойств самих макромолекул, так и от свойств разделяющей их среды - водного раствора. С этой целью исследовали влияние на конформационные колебания факторов - химических и физических, направленных как на макромолекулы белка, так и на разделяющий их растворитель. Результаты этих исследований были опубликованы в период 1964-1979 гг.
.Длительное время предполагалось, что "конформационные колебания" представляют собой специфическое свойство лишь фибриллярных белков актомиозинового комплекса. Однако в 1966 г. были обнаружены колебания (флуктуации) в растворах глобулярного белка - фермента креатинкеназы /Четверикова и др., 1967/. В дальнейшем на основе больших серий опытов с множеством разных препаратов было показано, что “"макроскопические флуктуации" являются общим свойством всех белков” /Шноль, Иванова и др., 1980/. При этом выяснилось, что макроскопические флуктуации не проявляются при денатурации белков /Рыбина и др., 1979/.
Однако исследования постепенно вышли за пределы белковых препаратов, поскольку выяснилось, что аналогичные "макроскопические флуктуации" наблюдаются и в безбелковых системах, и в частности, в колебаниях реакционной способности при взаимодействиях аскорбиновой кислоты с дихлорфеноминдофенолом /Рыбина и др., 1979/. Поэтому уже в 1980 г. сформировалось мнение, что “нативные макромолекулы белков являются лишь индикаторами идущих и без них макроскопических флуктуаций” /Удальцова и др., 1987, с.5/. И действительно, к 1982 г. макроскопические флуктуации (МФ) были обнаружены при измерениях таких разных процессов, как электрофоретическая подвижность клеток и частиц латекса, времени спин-спиновой релаксации Т2 протонов воды, флуктуации спектральной чувствительности глаза, времени разряда КС-генератора на неоновой лампе, а также при измерениях радиоактивного распада. Выяснилось, что большое сходство обнаруживают гистограммы МФ не только качественно различных процессов, исследуемых в одной лаборатории, но и процессов, исследуемых в лабораториях, отстоящих друг от друга на тысячи километров. Синхронными оказались и изменения гистограмм макрофлуктуаций разных и, в том числе, разнесенных на большие расстояния, процессов. Выявленные особенности макрофлуктуаций навели исследователей на мысль о том, что это явление имеет какие-то глобальные космофизические причины (См.:/Шноль и др., 1985; Удальцова и др., 1987/).
При этом были обнаружены весьма интересные особенности этого феномена.
1/ "Эффект места". В процессе исследования было обнаружено устойчивое различие характеристик макрофлуктуаций при измерениях в разных местах лабораторного помещения. Характеризуя этот эффект, авторы пишут: “Устойчивые воспроизводимые различия формы гистограмм наблюдались в многодневных опытах при помещении сосудов с соответствующими растворами на разные места одного и того же лабораторного стола, при расстоянии между сосудами около 30-40 см. Эти "эффекты места" не исчезали при экранировании сосудов стальными, заземленными экранами и не изменялись в зависимости от расположения в лабораторном помещении магнитов, трансформаторного железа, нагревательных приборов...” /Удальцова и др., 1987, с.17/.
Авторы указывают на то обстоятельство, что существенные различия гистограмм измерений образцов, стоящих на одном лабораторном столе, сочетаются с высокой степенью совпадения формы гистограмм результатов измерений МФ разных процессов на расстояниях в сотни и тысячи километров.
Дело обстоит так, как если бы пространство имело такую ячеистую структуру, в которой каждая ячейка дает вполне определенную форму гистограмм макроскопических флуктуаций качественно различных процессов и явлений, находящихся в этой ячейке. Авторы предполагают, что существует небольшое число разных вариантов этих ячеек и достаточно велика вероятность того, что на больших расстояниях исследуемые объекты оказываются в одинаковых ячейках пространства, дающих при синхронных измерениях одинаковые формы гистограмм макрофлуктуаций.
2/ Попытки экранировать исследуемые объекты при помощи экранов из разных материалов привели исследователей к выводу о том, что эти явления не обусловлены электромагнитными полями, поскольку не обнаружено соответствующей зависимости от материала экрана /Удальцова и др., 1987, с.17/.
3/ Интересные результаты получены при исследованиях корреляции параметров МФ с космофизическими процессами. Так, оказалось, что для биохимических и химических процессов среднегодовые значения макрофлуктуаций изменяются противофазно характеристике солнечной активности, т.е. “в годы с высокой солнечной активностью средняя амплитуда МФ была низкой и, наоборот, в годы низкой солнечной активности наблюдался весьма большой "разброс результатов" измерений биохимических и химических процессов” /Там же, с.19/. Авторы при этом отмечают, что из всех известных космофизических процессов в такой же зеркальной противофазности к солнечной активности находится интенсивность потока нейтронного компонента галактических космических лучей.
С точки зрения возможности синхронизации процессов протекающих в разных клетках живого организма, большой интерес представляют проведенные в 1951-1961 годах исследования концентрации различных веществ в крови живых организмов /Шноль, Гришина, 1964/. Обнаруженные в этих опытах резкие флуктуации содержания в крови разных веществ “пытались объяснить ритмической активностью печени, поглощающей и отдающей в кровоток различные вещества, или же ритмическим изменением адсорбционной способности эндотелия кровеносных сосудов” /Удальцова и др., 1987, с.66/. Рассматривая результаты этих исследований в свете открытых позже макрофлуктуаций, Н.В. Удальцова, В.А. Коломбет и С.Э. Шноль отмечают, что “... самым удивительным в тех опытах была необъяснимая синхронность изменений в концентрации крови различных веществ у разных животных”, и пишут, что теперь на основе результатов исследований феномена макрофлуктуаций “эту синхронность можно объяснить общей внешней причиной, одновременно изменяющей, например, адсорбционную способность (электрический заряд) эндотелия сосудов разных животных” /Там же/.
Но если имеет место синхронизация биохимических и биофизических процессов, протекающих в разных организмах, то тем более правомерно предполагать возможность синхронизации одинаковых процессов, протекающих в разных клетках одного и того же организма.
Несмотря на более чем 30-летний срок исследований макроскопических флуктуаций (МФ), этот феномен еще до сих пор не получил своего удовлетворительного объяснения. Можно лишь считать достаточно обоснованным вывод о том, что под влиянием каких-то космических "сил" все объекты окружающего нас макромира постоянно меняют свои состояния, что проявляется в виде макроскопических флуктуаций тех или иных характеристик этих объектов и протекающих в них физических и химических процессов.
Результаты исследований лаборатории С.Э. Шноля не оставляют сомнений в том, что, какова бы ни была природа этих сил, МФ могут иметь важное значение для временной организации физиологических процессов, выступая в качестве фактора, обеспечивающего синхронизацию однотипных процессов, протекающих в разных клетках многоклеточного сложного живого организма. При этом речь идет не о том, что эти процессы должны синхронизироваться в обычном физическом времени. В данном случае "синхронизация" означает, что многоступенчатые циклические процессы в разных клетках протекают таким образом, что одни и те же их ступени в разных клетках протекают когерентно, т.е. одномоментно, хотя при этом длительности как всего цикла, так и отдельных его этапов не остаются постоянными величинами в единицах физического времени, а меняются случайным, однако, одинаковым для всех клеток образом. Если такая синхронизация однотипных колебательных процессов живого организма имеет место в действительности, то введенное выше понятие внутриклеточного метаболического времени может оказаться предельно мелким масштабом (“ тонкой структурой” ) биологического времени сложных живых организмов как единых целостных систем.
Таким образом, имеются определенные основания предполагать синхронное следование квантов биологического времени во всех клетках многоклеточного живого организма. Это позволяет подойти к решению проблемы одновременности пространственно удаленных друг от друга процессов живого организма принципиально иначе, чем аналогичная проблема решается в физическом мире.
Как известно, в абсолютном времени классической физики существовала абсолютная одновременность событий, протекающих в сколь угодно удаленных друг от друга точках мирового пространства. Это означало, что все события мироздания однозначно делятся на прошедшие, настоящие и будущие.
Подобные представления оставались общепринятыми, пока не появилась позитивистская идея о необходимости их экспериментальной проверки и обоснования. Анализ показал, что в их основе лежит только априорная уверенность в том, что одновременными являются те события, которые могут быть охвачены единым актом сознания. В реальной действительности абсолютная одновременность и однозначное деление всех событий на прошедшие, настоящие и будущие оказываются эмпирически достоверными только при условии, что взаимодействие и обмен информацией между событиями происходит с бесконечной скоростью. При любых конечных скоростях взаимодействия требование эмпирической проверяемости временных отношений между событиями приводит к появлению класса событий, между которыми не существует отношения "раньше (позже), чем", и характер временных отношений между ними оказывается неопределенным.
В специальной теории относительности (СТО) одновременные пространственно удаленные друг от друга события выявляются в ходе синхронизации связанных с этими событиями часов. Предложенная А. Пуанкаре и использованная А. Эйнштейном при разработке СТО процедура синхронизации пространственно удаленных друг от друга часов сводится к следующему.
Пусть в точке А имеются некоторые часы и "точно такие же часы" имеются в точке В. Тогда наблюдатели в точках А и В будут фиксировать события в "А-времени" и "В-времени". Общее для точек А и В время, считает А. Эйнштейн, можно установить, если ввести определение, что "время", необходимое для прохождения света из А в В, равно "времени", требуемому для прохождения света из В в А /Эйнштейн, СНТ, т., 1, с. 9/. Пусть в момент
При этих условиях практически добиться того, чтобы часы в точках А и В показывали одно и то же время, можно следующим образом. Пусть между наблюдателями, находящимися в точках А и В, имеется договоренность о том, что наблюдатель в точке В в момент отражения сигнала от В к А выставляет на своих часах заранее договоренное с наблюдателем точки А показание, например, 00 часов, 00 минут, 00 секунд. В этом случае наблюдатель в точке А знает, что часы в точке В в момент (
Именно такой смысл вкладывает А. Эйнштейн в понятие одновременность. Вполне естественно, что если указанным выше образом синхронизировать часы во всех точках инерциальной системы отсчета, то все они будут одномоментно показывать одно и то же время, и мы введем некоторый аналог абсолютного времени, в котором существует "абсолютная одновременность" (одни и те же показания часов) и однозначное деление всех событий на прошедшие, настоящие и будущие. Однако подобная "одновременность" событий в масштабах всей инерциальной системы не имеет в физическом мире практического значения, поскольку при таком способе разграничения всех событий на прошедшие, настоящие и будущие далеко не для всех событий разнесенность их в разные времена означает возможность установления однозначных причинно-следственных связей
между ними. Так, например, все события, которые имели место в точке А в период, начиная с момента посылки светового сигнала в точку В и до возвращения в точку А отраженного сигнала, не могут иметь причинно-следственных связей с событиями, которые имели место в точке В в момент отражения пришедшего из точки А светового сигнала.В литературе, посвященной философским проблемам теории относительности, понятие “ одновременность” получило более широкое толкование, а именно, как совокупность таких событий, между которыми не может быть причинно-следственных связей, а следовательно, и однозначных временных отношений, если временные отношения между событиями связывать с реальными или, по крайней мере, потенциально возможными между ними причинно-следственными связями. При таком причинном определении временной последовательности событий все те события, между которыми не могут существовать материальные взаимодействия, можно рассматривать как релятивистский аналог “ всемирной одновременности ньютоновской физики” /Уитроу, 1964, с. 389/ и называть либо “ квазиодновременными” /Фок, 1961, с. 52/, либо “ топологически одновременными” /Грюнбаум, 1969, с. 44-48, 435-505/. Учитывая это, мы назовем одновременность, определенную как одинаковые показания синхронизированных между собой часов,
“ формальной одновременностью” .В физическом мире “ формальная одновременность” не имеет физического смысла. Совершенно иначе обстоит дело в живом организме, в котором каждая клетка содержит копию одной и той же генетической программы, и если эта программа закодирована в единицах метаболического времени, то при существовании формальной одновременности все клетки организма могут точно одновременно совершать те или иные акты при условии, что счет времени ведется непрерывно с самого начала эмбрионального развития организма.
Итак, мы рассмотрели некоторые данные современной биологии, позволяющие сделать вывод о том, что биологические процессы живого организма структурированы в особом биологическом времени.
Наиболее глубинным, фундаментальным уровнем временной организации биологических процессов живой материи является уровень ферментативных реакций внутриклеточного метаболизма. Именно здесь необходимо искать далее неделимые кванты биологического времени, на протяжении которых протекающие в весьма своеобразно организованной и резко изменяющей свои свойства внутриклеточной среде физические и физико-химические процессы интегрируются в элементарные акты биологических процессов.
Квантованность биологического времени может иметь важное значение для генетики, а также для теоретической биологии. Однако для целей практического хронометрирования биологических процессов необходимо искать более крупные единицы биологического времени, связанные с его квантами через постоянные масштабные коэффициенты. При этом не исключено, что может не оказаться таких доступных практическому счету единиц биологического времени, которые сохранялись бы на всех этапах развития живого организма.
Итак, нами обоснована принципиальная возможность существования качественно различных типов времени и показана правомерность введения в биологию понятия биологического времени. Однако проблема биологического времени нуждается в дальнейшей экспериментальной, теоретической и методологической разработке, поскольку введение в понятийный аппарат биологии понятия биологического времени - это серьезный шаг, требующий решения сложных и трудоемких задач, связанных с разработкой систем единиц биологического величин, установлением специфических законов биологической формы движения материи, а также с разработкой принципиально новых приемов и методов исследования живой материи.
1. На протяжении всей истории развития понятия времени и по сей день равномерность рассматривают как одно из важнейших свойств времени, предполагая, что все материальные процессы можно однозначно разделить на равномерные и неравномерные. Однако анализ понятия и критериев равномерности убеждает, что равномерность есть соотносительное свойство сравниваемых между собой материальных процессов и что в принципе возможно существование неограниченного множества удовлетворяющих критериям равномерности классов соравномерных процессов, каждый из которых в соответствующей области материальной действительности пригоден для введения единиц измерения длительности и практического измерения времени.
2. Основные материальные процессы, при помощи которых измеряется физическое время, представляют собой механические движения закрытых консервативных динамических систем, которые благодаря сохранению неизменной механической энергии могут неограниченно долго (в идеале) продолжать движение без изменения параметров, что и делает их соравномерными.
3. Равномерность физического времени обеспечивается подчиненностью закрытых консервативных динамических систем закону сохранения энергии.
4. Классы соравномерных процессов могут существовать в таких целостных высокоинтегрированных материальных системах, в которых материальные процессы настолько тесно взаимосвязаны и сопряжены, что ведут себя как единый поток, синхронно и пропорционально ускоряясь и замедляясь под воздействием различных и, в том числе, случайным образом изменяющихся факторов. Именно такими системами являются живые организмы. О наличии в живых организмах классов соравномерных биологических процессов свидетельствуют результаты исследований биологов, описывающих развитие живых организмов в специфических единицах длительности. Биологическое и физическое время взаимно стохастичны, поскольку единицы биологического времени представляют собой длительности таких повторяющихся биологических процессов, которые, будучи измеренными в единицах физического времени, меняются случайным образом, в зависимости от случайных изменений характеристик окружающих условий.