Гелиогеофизические эффекты нелокальности – тени будущего в настоящем

c.м. коротаев

Доктор физико-математических наук

(Получена 12 августа 2004; опубликована 13 августа 2004)

Есть основания полагать, что вопреки распространенному мнению явление нелокальности может выходить на макроуровень, приводя к корреляции практически изолированных диссипативных процессов. Хотя последовательная теория такого выхода отсутствует, можно предложить эвристическую модель, проверяемую экспериментально. Такие эксперименты были поставлены. Обнаружено наличие нелокальных корреляций крупномасштабных природных процессов с пробными лабораторными процессами. Наиболее интересным их свойством оказалось наличие опережающего лага, что позволяет, в некотором смысле «видеть» неконтролируемое наблюдателем будущее.

Странные корреляции

За последние десятилетия в геофизике и астрофизике накоплен ряд статистически достоверных фактов зависимостей удаленных необратимых процессов различной природы, которые не могут иметь ни прямой, ни опосредованной связи на основе известных (электромагнитных и гравитационных) взаимодействий. Сюда относятся, например, неприливная компонента зависимости сейсмичности Земли и Луны, зависимость скорости некоторых физико-химических реакций от солнечной активности, зависимость скорости геологической седиментации от той же солнечной активности, зависимость вариаций мюонов космических лучей и естественной радиоактивности горных пород [1,2]. Такие коррелирующие процессы могут иметь самую различную природу, единственное, что их роднит - это существенная диссипативность (необратимость).

Эти странные корреляции обнаруживались учеными различных специальностей - астрономами, физиками, химиками, геологами, геофизиками и долгое время оставались разрозненными, поскольку оставались известными разобщенным узким кругам специалистов. В последние годы "критическая масса" фактов была достигнута, стала видна их общность и, тем самым, обострилась необходимость целенаправленного изучения. При этом проявились три подхода.

Первый подход: "механизм корреляций неизвестен, но не нов". Под "неизвестным" предполагалось некоторое "слабое низкочастотное электромагнитное поле". Характерно, что это предположение выдвигалось именно неспециалистами по электромагнитному полю. Мне, как специалисту как раз по электромагнитному полю, не раз приходилось сталкиваться с тем, что многим людям свойственно все загадочное и непонятное ассоциировать именно с ним. Вероятно, корни таких ассоциаций уходят к Мессмеру с его "животным магнетизмом". В нашем случае для специалиста очевидно, что не может быть и речи о связи удаленных неэлектромагнитных процессов через слабое, иногда им сопутствующее, электромагнитное поле. Это поле безнадежно слабо часто даже для измерения, не говоря о том, чтобы оно могло на что-то повлиять. А на радиоактивные процессы такое влияние в принципе исключено.

Второй подход наиболее ярко представлен С.Э. Шнолем, декларирующим вслед за Ньютоном: "гипотез не измышляю". В течение полувека С.Э.Шноль и его коллектив провели огромный объем исследований, доказавших связь флуктуаций различных изолированных лабораторных необратимых процессов между собой и с космофизическими факторами [3]. Этот путь к настоящему времени успешно завершен, достоверность связей доказана и вопрос о их физике встал с особой остротой.

Третий подход - поиск принципиально нового механизма связи изолированных диссипативных процессов. Логика этого подхода такова: наблюдательные астрофизические и геофизические данные могут лишь навести на существование такого механизма, далее на основе некоторых постулатов должна быть развита теория, предсказывающая определенные следствия, подлежащие экспериментальной верификации. Если в числе этих следствий окажутся упомянутые корреляции процессов, значит, механизм найден. Этот подход связан, прежде всего, с именем Н.А. Козырева [1]. Хотя основным наблюдательным мотивом для начала построения теории, названной им причинной механикой, были не те самые корреляции, которые интересуют нас, а другие интригующие астрофизические закономерности, важно, что «на выходе» у него оказались именно эффекты взаимодействия практически изолированных необратимых процессов. Основным постулатом причинной механики является признание фундаментальной асимметрии времени (отсутствующей в общепринятом описании основных физических взаимодействий кроме слабого). Это, в конечном счете, и привело Н.А. Козырева к выводу о взаимодействии изолированных необратимых процессов, который проверялся в обширной серии лабораторных и астрофизических экспериментов. Мало того, признание фундаментальной асимметрии времени парадоксальным образом привело к выводу, что для неконтролируемых наблюдателем процессов должно существовать взаимодействие в обратном времени, что также было подтверждено экспериментально [4-6]! Результаты были настолько неожиданны, что встретили, в целом, негативную реакцию. Одной из причин было сомнение в чистоте его экспериментов (хотя никто не взял на себя труд по их проверке). Положение стало меняться, как водится, после смерти автора. Эксперименты Н.А. Козырева были успешно воспроизведены в различных лабораториях мира. Однако сомнения в их чистоте остались. Действительно, большинство экспериментов Н.А. Козырева было поставлено явно нестрого, а его последователи остались на том же (или худшем) уровне. Поэтому, хотя до середины 90-х годов возможная причинномеханическая природа странных корреляций изолированных процессов многократно обсуждалась в научных аудиториях, вопрос оставался открытым.

Целью исследования, поставленного в Институте геоэлектромагнитных исследований РАН (ИГЭМИ), была проверка гипотезы о причинномеханической природе корреляций некоторых гелиогеофизических процессов. Основой такой проверки должен был стать натурный эксперимент, поставленный на современном уровне строгости.

Формулировка гипотезы

Прежде чем ставить эксперимент, надо было очень четко сформулировать проверяемую гипотезу. Мало просто предположить наличие нового взаимодействия, это предположение должно быть связано с представлениями современной физики. Должен выполняться принцип соответствия - введение в рассмотрение неклассического взаимодействия должно предусматривать предельный переход к его отсутствию в классике.

Результаты Н.А. Козырева и его последователей (Д. Сэвидж, М.М. Лаврентьев и др., например, [7,8]) могут быть обобщены в следующих положениях:

1. Существует принципиально новый тип взаимодействия между необратимыми процессами любой природы.

2. Это взаимодействие осуществляет передачу энергии, момента импульса, но не импульса.

3. Энергия взаимодействия прямо связана с производством энтропии и обратна квадрату расстояния.

4. Взаимодействие экранируется веществом, однако экранирующие свойства вещества отличаются от этих свойств для электромагнитного поля.

5. Взаимодействие может идти с запаздыванием, мгновенно и с симметричным опережением.

Выписав эти положения, мы увидели, что за исключением ссылки на необратимость, все это очень напоминает квантовую нелокальность - эффект, восходящий к парадоксу Эйнштейна-Подольского-Розена (предложенного ими в оставшихся навсегда знаменитыми спорах о состоятельности квантовой механики). Суть эффекта в том, что разлетевшиеся на любое расстояние частицы, имеющие общую волновую функцию, т.е. находящиеся в запутанном состоянии, способны, без посредства каких-либо промежуточных носителей, обмениваться информацией через пространственно-подобный интервал, т.е. со сверхсветовой скоростью. Правда, чтобы расшифровать эту информацию, надо, кроме этого нового нелокального канала ее передачи, иметь классический (локальный, досветовой) канал. Эффект нелокальности блестяще подтвержден во многих экспериментах и интенсивно исследуются в настоящее время, в том числе, в связи с практическими приложениями. Предсказана временная симметрия квантовых корреляций – запутанные состояния формируются не только после локального взаимодействия частиц но и до него [9]. При заметном сходстве с козыревским взаимодействием есть важное но: до последних лет считалось, что нелокальность наблюдаема только на уровне отдельных частиц, но на макроуровне ее заметить нельзя. Однако недавно теоретические разработки различных ученых, в первую очередь, индийских физиков Д. Хома и А. Маюмдара [10] показали, что эффект нелокальности должен как-то сохраняться и в сильном макропределе, хотя идея экспериментальной проверки не была ими предложена. Но мало того, что козыревское взаимодействие имеет место для макроскопических процессов, эти процессы должны быть существенно диссипативными. Между тем, известно, что диссипативность ведет к декогерентции – разрушению квантовых корреляций. И только, опять таки, совсем недавно российским физиком А.М. Башаровым было показано, что диссипативность процессов при наличии общего термостата (которым может быть электромагнитное поле) играет как раз конструктивную роль в формировании квантовых корреляций [11].

В этом месте пора сделать терминологическое отступление. Хотя выше и далее говорится о нелокальном взаимодействии, в квантовой механике принято говорить о нелокальных (квантовых) корреляциях. Причина в том, что нелокальная связь не может существовать в отрыве от какого-либо из четырех известных фундаментальных взаимодействий, так что не может считаться пятым (это «пятое» тоже ищут, но то уже совсем другая история). Корреляция тоже не лучший термин, поскольку возникает не обязательно из прямой физической связи, которая имеет место в явлении нелокальности. Поэтому в англоязычной литературе для такого рода необычного взаимодействия сейчас применяют термин не «interaction», а «transaction». Увы, последний термин в русском языке уже оккупирован финансистами. Так что, за неимением точного русского эквивалента будем все же говорить о «взаимодействии», где по-английски сказали бы «transaction».

Сама по себе квантовая механика описывает эффект нелокальности, но его интерпретация является предметом дискуссии. Одна из перспективных интерпретаций предложена американским физиком Дж. Крамером [12]. Он предложил объяснение эффекта нелокальности в рамках теории прямого межчастичного взаимодействия Уилера-Фейнмана. Это единственная физическая теория, согласующаяся с экспериментом, предусматривающая существование, наряду с запаздывающим, опережающего поля (т.е. в буквальном смысле сигналов идущих в обратном времени). В результате интерференции полей всех зарядов опережающие поля в точности гасятся, и единственным наблюдаемым результатом их существования является эффект радиационного затухания. Но с последним связан любой необратимый процесс. Это создает предпосылку для объяснения самого поразительного, последнего в нашем списке свойства козыревского взаимодействия - симметричного запаздывания и опережения (мгновенное взаимодействие тогда может быть кажущимся - результатом интерференции запаздывающего и опережающего). Современное развитие теории прямого межчастичного взаимодействия предпринятое выдающимся английским астрофизиком Ф. Хойлом и индийским Дж. Нарликаром [13] показало, что запаздывающее и опережающее электромагнитные поля асимметричны (и в этом проявляется постулированная Н.А. Козыревым асимметрия времени) - первое обязано в конечном счете полностью поглотиться веществом, а второе нет. Это указывает на возможность объяснения и предпоследнего в нашем списке свойства козыревского взаимодействия.

Синтез идей причинной механики, квантовой нелокальности и теории прямого межчастичного взаимодействия позволил нам сформулировать гипотезу в виде уравнения макроскопической нелокальности:

, ,

где - производство энтропии в пробном процессе (детекторе), s - сечение взаимодействия, ħ - постоянная Планка, m_e - масса электрона, c- скорость света, - плотность производства энтропии в источниках, x- расстояние, t- время, n - эффективная скорость распространения, интегрирование ведется по объему источников V. d-функция показывает, что взаимодействие идет с симметричным запаздыванием и опережением. Если взаимодействие идет через среду диффузионным путем (через микроскопические электромагнитные поля Уилера-Фейнмана), то n будет мала и, следовательно, результирующие величины запаздывания и опережения будут велики. В классическом пределе (ħ ®0) эффект исчезает.

Но не зашли ли мы слишком далеко, рассуждая об опережающем взаимодействии? Как же быть с причинностью? В 1980г. Дж. Крамер ввел различие между принципами сильной и слабой причинности. Принцип сильной (или локальной) причинности звучит так: причина предшествует всем возможным следствиям. Это, по сути, и есть то, что обычно и обыватели, и физики называют «принципом причинности». А вот принцип слабой причинности: причина, инициированная наблюдателем, опережает все возможные следствия. Явление квантовой нелокальности нарушает сильную причинность при сохранении слабой. Это означает, что наблюдатель не может отправить «телеграмму в прошлое». Не может быть и такого, чтобы какой бы то ни было прибор отреагировал на включение источника воздействия, прежде чем вы нажмете кнопку включения. Но если процесс- источник спонтанный, реакцию на заранее неизвестное его будущее состояние наблюдать можно!

Поэтому наиболее интересны эксперименты именно со спонтанными процессами, на них были сосредоточены наши основные усилия, и именно о них пойдет дальнейший рассказ. Эксперименты с инициированными наблюдателем, т.е. контролируемыми процессами, разумеется, необходимы для сопоставления, и они также были выполнены, но в контексте данной статьи я ограничусь лишь упоминанием.

Как проверить гипотезу

Предварительные оценки, согласно нашему уравнению, показали, что разнообразные и постоянно идущие спонтанные геофизические и гелиофизические процессы должны давать больший эффект на детекторе, чем те, которые несложно создать в лаборатории. Стало понятно, почему случайные свидетельства существования предполагаемого нового эффекта появились именно в геофизике!

Задачей эксперимента является обнаружение связи изменения энтропии в некотором пробном процессе с изменением энтропии в окружающей среде в соответствии с уравнением нелокальности при исключении всех известных видов классического локального взаимодействия. Хотя в качестве пробного процесса в детекторе может использоваться любой необратимый процесс, непосредственно измеряется не энтропия, а некоторый косвенно связанный с ней наблюдаемый макропараметр. Поэтому вопрос о выборе типа детектора переходит в практическую плоскость: пробный процесс должен быть теоретически «прозрачен» (теория детектора должна позволять расчет левой части уравнения нелокальности по измеряемому сигналу и должен быть ясен полный список возможных локальных влияний на данный процесс. Детектор должен быть максимально чувствителен и, в то же время, допускать надежную экранировку от классических воздействий. Исходя из этого, в ИГЭМИ была построена установка на базе двух типов детекторов, основанных на связи энтропии с высотой потенциального барьера. В одном измерялись спонтанные вариации разности собственных потенциалов слабополяризующихся электродов в электролите (U), в другом - темнового ток фотоумножителя (I).

Источниками помех, т.е. локального воздействия, на эти детекторы являются изменения температуры, давления, электрического и магнитного поля и т.п. Эти факторы необходимо исключить, а если какой-либо из них не удается подавить полностью, он должен контролироваться. С этой целью были предприняты многочисленные меры, в частности оба детектора были помещены в дьюары, защищены многослойной экранировкой, возможные помехообразующие факторы непрерывно измерялись как в лаборатории, так и внутри корпусов детекторов. Так, пассивное термостатирование (активное здесь непригодно), сколь бы совершенным оно ни было, не может полностью подавить вариаций температуры, поэтому детекторы были снабжены внутренними термодатчиками, непрерывно измеряющими их температуру с точностью до тысячной градуса.

Установка измеряет также некоторые геофизические параметры, отражающие интенсивность естественных необратимых процессов. В частности, с помощью квантового магнитометра велись высокоточные измерения магнитного поля.

Важна не только техника эксперимента, но и методика анализа данных. Этот анализ несложен в случае искусственных контролируемымых процессов-источников или даже в случае естественных спонтанных процессов, когда последние представляют отдельные мощные кратковременные события, например, солнечные вспышки. Но, как правило, естественный процесс непрерывен, его нельзя выключить по желанию экспериментатора. В этом случае изучается корреляционная функция сигнала детектора и какого-либо характерного макропараметра процесса (индекса). При классическом локальном взаимодействии главный максимум модуля корреляционной функции будет всегда наблюдаться при запаздывании сигнала детектора (следствия) относительно индекса процесса- источника (причины). Вообще говоря, могут быть максимумы и в области опережения, но они связаны с периодической составляющей сигнала и в суммарном сигнале они всегда меньше запаздывающих. Если же опережающий максимум окажется статистически достоверно больше всех запаздывающих, значит, мы наблюдаем искомое неклассическое взаимодействие в обратном времени. Беда только в том, что хотя из теории Хойла-Нарликара действительно следует меньшая эффективность поглощения промежуточной средой опережающего поля по сравнению с запаздывающим (откуда вытекает неклассическая асимметрия корреляций), величину отношения эффективностей теория не предсказывает. Оно может быть близко к 1, поэтому полагаться только на корреляционный анализ нельзя. Вдобавок, чаще всего измеряемый макропараметр связан с производством энтропии нелинейно, поэтому корреляционная функция искаженно характеризует зависимость процессов.

На помощь приходит метод причинного анализа. Он был создан в свое время для формализации слишком интуитивных исходных положений причинной механики Н.А. Козырева [14]. Но оказалось, что он представляет инструмент очень полезный в широком круге задач, где необходимо разбираться, что является причиной, а что – следствием. Дело в том что, несмотря на широкое применение принципа (сильной) причинности, под ним понимается только запаздывание следствия относительно причины, что же такое «следствие» и «причина» остается формально неопределенным. Однако запаздывание является необходимым, но недостаточным условием причинной связи. Даже у юристов есть формула: «Post hoc non est propter hoc» (после того не значит вследствие того). А между тем, в ряде ситуаций разница между причиной и следствием очевидна, запаздывание подразумевается, но не измеряется. Например, включилась лампочка и сработал фотоэлемент. Очевидно, что ток в цепи лампочки – причина, ток в цепи фотоэлемента – следствие. Это значит, что причинно-следственная связь асимметрична и значит можно определить различие между причиной и следствием, а уже потом ввести запаздывание как аксиому.

Наши интуитивные представления можно формализовать следующим образом. Положим, есть два процесса X и Y, для них можно рассчитать их безусловные H(X), H(Y) и условные H(X÷Y), H(Y÷X) шенноновские энтропии. Отметим, что H - энтропии уровней, в отличие от фигурирующей в уравнении нелокальности энтропии положений, иначе говоря (безразмерной) термодинамической энтропии S; H и S имеют одинаковые математические формы, но отличаются пространствами определения вероятностей, их можно связать в рамках теории расслоенных пространств [19]. Можно определить пару функций независимости:

, , .

i_X_÷_Y = 0 соответствует однозначной зависимости X от Y, i_X_÷_Y = 1 – отсутствию зависимости X от Y (последнее также влечет i_X_÷_Y = 1). Грубо говоря, функции независимости ведут себя обратно корреляционной функции. Однако они асимметричны (в общем случае i_X_÷_Y ¹ i_Y_÷_X) и универсальны – равно пригодны для любых видов нелинейной (или линейной) связи X и Y. Их асимметрию характеризует функция причинности g:

, .

Мы определяем, что причиной Y и следствием X называются процессы, для которых g > 1. Если g < 1, то наоборот X - причина, Y - следствие. Если же g = 1, то связь X и Y непричинная (адиабатическая).

Теперь пусть t - сдвиг времени между Y и X (t = t_Y – t_X). Принцип сильной (локальной) причинности утверждает тогда, что если g > 1 то t < 0, если g < 1 то t > 0, если g ® 1, то t ® 0.

Этот подход можно обобщить и на множество процессов X,Y,Z,…, , образующих причинную сеть [17]. Заметим, что во всех случаях, когда разграничение процессов на причины и следствия очевидно, формальный расчет g дает результат, соответствующий интуитивно ожидаемому [15, 16, 18, 19].

Если Y - заведомо соответствует причине (например, Y - индекс солнечной активности), а X - следствию (X - сигнал детектора), то для любого классического взаимодействия главный min i_X_÷_Y будет наблюдаться при t < 0 и этому минимуму будет соответствовать главный max g > 1. Только при нелокальной корреляции процессов возможно g > 1 при t > 0.

Это и есть нужный критерий. Но, следуя традиции, наличие нелокальных корреляций следует проверить нарушением неравенства типа Белла. Такое неравенство в нашем случае выглядит так:

Оно означает следующее. Если Z может воздействовать на X только через Y по локальной причинной цепи Z®Y®X, то связь между Z и X будет слабее самой слабой из связей в звеньях Z®Y и Y®X. Представим, например, что в окружающей среде (в лаборатории) происходят случайные (спонтанные) вариации температуры. Это будет наш процесс Z. Процесс X - измеряемый макропараметр пробного процесса, например разность электродных потенциалов. Электроды находятся пассивно-термостатирующего контейнера, в котором отсутствуют собственные источники тепла. Вариации наружной температуры ослабляются внутри контейнера, но остаются конечными. Это будет наш промежуточный процесс Y. Z не может локально никак иначе повлиять на X как через Y. Только нелокальная связь может привести к нарушению записанного выше неравенства.

Эксперименты

Первый эксперимент по изучению эффекта нелокальности естественных процессов-источников выполнялся на установке ИГЭМИ в течение года (декабрь 1996 – декабрь 1997). В непрерывном режиме измерялись сигналы электродного детектора U, фотокатодного I, их внутренние температуры T_U и T_I, температура воздуха в лаборатории T_e и магнитное поле в непосредственной близости от детекторов B.

Предварительные оценки показали, что наибольший вклад в сигналы детекторов должны вносить процессы синоптической и солнечной активности. В эксперименте в качестве макропараметров этих процессов мы использовали, соответственно, приземную температуру T_a и давление P в Москве и поток солнечного радиоизлучения на 11 стандартных частотах в диапазоне 245–15400 МГц. Измеренные на установке вариации геомагнитного поля (B) характеризуют заведомо более слабый, но удобный для количественной интерпретации процесс омической диссипации магнитосферно-ионосферных токов. Чтобы подчеркнуть масштаб этого процесса оказалось целесообразным использовать также Dst-индекс глобальной геомагнитной активности (рассчитываемый по данным экваториальных обсерваторий и характеризующий наиболее крупномасштабные токи в магнитосфере). Рассматривались также некоторые другие процессы, о чем будет речь далее.

Этот эксперимент был первым. Но как будет рассказано в следующем разделе, идеи, во-первых, носятся в воздухе и реализуются независимо разными исследователями – за счет этого материалы эксперимента оказались богаче; во-вторых, под идею можно иногда приспособить эксперименты, выполненные с другими целями – за счет этого мы получили вторую серию измерений с устройством подобным нашему электродному детектору, естественно, худшего качества, но за более длительный срок (1993 – 1997).

Третья серия измерений с электродным детектором установки ИГЭМИ начата в октябре 2001г. и представляет наиболее длительный целенаправленный эксперимент.

В следующем разделе кратко описываются результаты, вытекающие из анализа данных первых двух серий и немного - третьей, которые на момент написания этой статьи еще обрабатываются. Полное описание приведено в работах [20-31].

Кроме того, выполнялись также эксперименты с контролируемыми (искусственными) процессами-источниками. Эти эксперименты методически сложнее – применяется дифференциальная схема измерений для исключения влияния природных источников, требуются дополнительные меры для исключения локального воздействия близких и мощных искусственных источников. При этом наблюдается, естественно, только запаздывающая реакция детекторов. Поэтому я не буду здесь касаться их результатов (подробно опубликованных в [32,33]) отмечу лишь, что они подтвердили, в основном, соответствующие результаты Н.А. Козырева.

Результаты

Корреляция сигналов на различных детекторах. Прежде всего, имело смысл сравнить измерения обоих детекторах установки. Это сразу позволяет проверить, а не являются сигналы столь надежно защищенных от внешних шумов детекторов их чисто внутренними шумами? Оказалось, что сигналы внешнего происхождения действительно есть - коэффициент корреляции сигналов обоих детекторов достигает 0,75±0,01. Но может быть в этом виноват тривиальный общий фактор - вариации лабораторной температуры, которые, пусть в сильно подавленном виде, проникают внутрь дьюаров? Оказалось, что при математическом исключении влияния лабораторной температуры, корреляция лишь увеличивается (0,78±0,01). Таким образом, тривиальный общий фактор не является общей причиной. Это иллюстрирует рис.1, на котором показаны синхронные амплитудные спектры сигналов детекторов U и I и лабораторной температуры Т_е в диапазоне периодов от 5 часов до 10 суток. Видно, что спектры U, I подобны, спектр Т_е выглядит совершенно иначе.

Рис.1. Амплитудные спектры сигналов электродного U и фотокатодного I детекторов и лабораторной температуры Т_е (t – период в часах).

По стечению обстоятельств, в течение части срока нашего эксперимента и совершенно независимо сходные измерения собственных потенциалов электродов в других целях выполнялись сотрудником ИГЭМИ В.И. Наливайко. Его установка размещалась в другом здании в 300 м от нашей. Она не предусматривала мер защиты от помех подобных нашим, но если полезный сигнал, связанный с крупномасштабными геофизическими процессами, в вариациях потенциалов U достаточно велик, можно было рассчитывать на корреляцию с нашими данными. Так оно и оказалось - корреляция достигала 0,68±0,01, а при исключении влияния внутренней температуры 0,74±0,01. Таким образом, локальное влияние температуры не является общей причиной коррелирующих вариаций потенциалов. Такой общей причиной остается считать нетривиальное воздействие геофизических процессов. А факт высокой корреляции электродных потенциалов позволил нам использовать и предыдущие измерения В.И. Наливайко (с 1993г.) для сопоставления с гелио-геофизическими данными.

Когда наш эксперимент был уже закончен, я неожиданно узнал, что в течение части срока наших измерений подобный эксперимент (на иных технических принципах, но с той же целью) выполнялся в Центре прикладной физики (ЦПФ) МГТУ им. Н.Э. Баумана под руководством профессора А.Н. Морозова. Установка ЦПФ включала детектор, в котором производство энтропии связано не с высотой потенциального барьера, а с флуктуациями подвижности ионов в электролите. Уровень защищенности от помехообразующих факторов был сопоставим с нашим. Расстояние между установками ЦПФ и ИГЭМИ 40 км. Выполнив, совместно с А.Н. Морозовым, сопоставление синхронных данных детекторов, мы получили коэффициент корреляции 0,715±0,005. Это окончательно убедило в наличии нетривиального влияния на детекторы общих крупномасштабных процессов.

Далее рассмотрим влияние основных групп таких процессов, опуская детали связанные с нелегкой, но вполне рутинной задачей разделения сигналов.

Синоптическая активность. Энтропия окружающей среды изменяется при изменениях температуры, фазовых переходах и т.п. Изменения температуры как индикатор изменений энтропии качественно наиболее удобны, т.к. происходят непрерывно и легко доступны измерению. При этом окружающая среда включает три обособленных масштаба: собственно геофизический - синоптический масштаб (амплитуда ~10 К), масштаб лаборатории (~1 К) и, наконец, масштаб самого детектора (~0,1 К). Начнем с последнего.

Вследствие малости амплитуд внутренней температуры детектора Т_U из обычных представлений следовало ожидать небольшой отрицательной (таков знак температурного коэффициента электродов) корреляции потенциалов U и температуры Т_U с запаздыванием U относительно Т_U порядка десятка часов (в соответствии с тепловой инерцией электролита). И действительно оказалось, что для электродного детектора запаздывающая корреляция равна – 0.33±0.02 при запаздывании на 20.4 ч. Но в области опережения, где корреляция классически должна затухать, обнаружился необычный максимум корреляции 0.87±0.01 при опережении на 12.8 ч. При тех же временных сдвигах обнаруживаются и минимумы функций независимости, причем опережающий минимум значительно глубже. Анализ связи сигнала с внешней температурой Т_е показал наличие трех максимумов корреляции (минимумов независимости) при сдвигах 0 и ±27 ч. Самым большим оказался опережающий максимум, вследствие чего он не мог быть объяснен каким-либо эффектом периодичности. Такая картина соответствует теоретическому предсказанию: мы наблюдаем симметричное запаздывание и опережение, опережающий сигнал сильнее вследствие меньшего поглощения промежуточной средой. Наличие кажущегося синхронного сигнала может быть объяснено интерференцией запаздывающего и опережающего сигналов. Подробный анализ взаимодействия Т_е, Т_U, U в прямом и обратном времени, с учетом того что Т_U только запаздывает относительно Т_е (в среднем на 11.5 ч) позволил количественно объяснить и асимметрию связи U с Т_U при симметрии U с Т_е.

Комбинация измерений внешней и внутренней температур и сигнала детектора позволила провести тест на нелокальность корреляций по нарушению неравенства типа Белла в том самом виде, как это было разобрано в предыдущем разделе. Оказалось, что имеются два канала связи сигнала детектора с внешней температурой: классический локальный запаздывающий и необычный нелокальный опережающий. Для первого это неравенство выполняется, для второго – нарушается.

Рассмотрим теперь изменения атмосферной температуры Т_а как пример крупномасштабного (сотни км) геофизического процесса. Учитывая термостатирование, локальная причинная связь Т_а®Т_е®Т_U®U может приводить лишь к слабой корреляции потенциалов U с атмосферной температурой Т_а с многосуточным запаздыванием. Для исключения возможного влияния мелкомасштабных неоднородностей, в качестве Т_а мы взяли измерения атмосферной температуры выполненные в 40 км от нашей установки (вблизи установки ЦПФ). В этом случае обнаружены симметричные по сдвигу времени опережающие и запаздывающие корреляции, при этом уровень опережающих, примерно, вдвое выше уровня запаздывающих. Максимум корреляции (0.73±0.01) наблюдается при опережении сигнала на 13 дней. Если же в качестве индекса взять атмосферное давление (масштаб порядка тысяч км) пик корреляции достигает – 0.86 при опережении 2.5 месяца. Аналогичное соотношение наблюдается для функций независимости и причинности. Последние, как указывалось в предыдущем разделе, более адекватны для выявления эффекта нелокальности, поэтому рассмотрим пример результата их расчета на рис.2. Самый глубокий минимум функции независимости i_U_÷_P »0.30 и наивысший пик функции причинности g = i_P_÷_U /i_U_÷_P »2.3 наблюдаются при опережении t =69 сут.

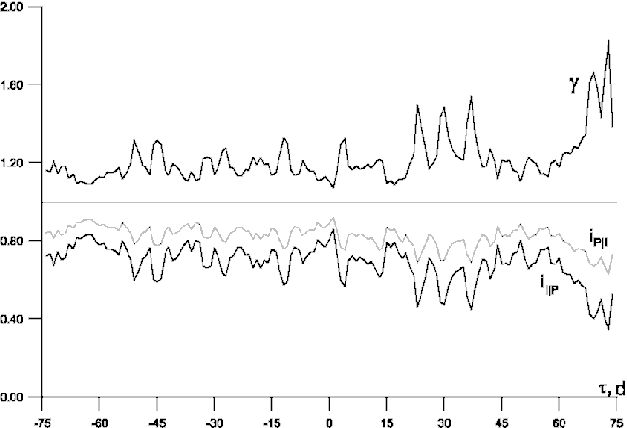
Рис.2. Функции независимости и причинности сигнала электродного детектора U за март - апрель 1997 и атмосферного давления P (t - временной сдвиг в сутках; t < 0 соответствует запаздыванию, t > 0 - опережению U относительно P).

Этот результат не зависит от типа детектора. На рис.3 показан тот же пример с фотокатодным детектором. Картина подобна и опережение почти то же (t=73 сут.).

Рис.3. Функции независимости и причинности сигнала фотокатодного детектора I за март – апрель 1997 и атмосферного давления P.

Возможно даже дать простейший прогноз. На рис.4 для того же примера показана временная вариация давления (прохождение циклона) и предшествующая на 73 дня вариация темнового тока.

Рис.4. Вариация сигнала детектора I, прогнозирующая вариацию давления P с заблаговременностью 73 сут. Начало отсчета времени (в сутках) соответствует 24 марта 1997.

Итак, во всех этих случаях (и во всех прочих изученных, рассматриваемых ниже) наблюдается опережающая реакция детектора на диссипативный процесс. Очень важно, что детектор реагирует не на предвестник в обычном прогностическом смысле (т.е. не как барометр на предстоящее изменение погоды). Как ни странно это звучит, детектор реагирует на будущее состояние процесса как на существующую реальность. Мы наблюдаем своего рода тени будущего!

Геомагнитная активность. В качестве геофизического процесса иного рода рассмотрим процесс диссипации токов, связанных с геомагнитными вариациями. Дело в том, что величина сигнала электродного детектора U теоретически никак не должна быть связана с магнитным полем В (фотокатодный детектор, хотя и в ничтожной степени для геомагнитного поля уязвим). Поэтому хорошим тестом для нашей гипотезы было бы обнаружение корреляции U с естественными вариациями магнитного поля Земли, поскольку эти вариации легко могут быть связаны с омической диссипацией в источниках поля. На всякий случай было проверено влияние искусственного магнитного поля на детектор. Никаких следов такого влияния замечено не было даже в весьма сильном поле - на пять порядков большем характерного для геомагнитных вариаций.

Анализ показал, что искомая корреляция есть, причем ее единственно значимый пик (-0.56±0.01) наблюдается при опережении U относительно В на двое суток, запаздывающая корреляция полностью подавлена.

В рассмотренных ранее синоптических процессах энтропия зависит от температуры, давления, но не только от них и установить эту зависимость количественно, учитывая весь комплекс процессов в атмосфере и подстилающей Земле, крайне затруднительно. В этом смысле производство энтропии в процессе диссипации токов, возбуждающих геомагнитные вариации, гораздо удобнее. Это дает возможность количественно проверить уравнение макроскопической нелокальности.

Уравнение макроскопической нелокальности совместно с теорией электродного детектора и теоретической моделью источника магнитного поля дает важное предсказание: отношение спектральных амплитуд потенциалов и геомагнитного поля U/B зависит от периода вариаций, но U/B²от периода не зависит.

Указанная зависимость обнаружилась. Любопытно, что эта зависимость соответствует фликкер-шуму, т.е. отношение амплитуд U/B пропорционально корню из периода, соответственно отношение спектральных плотностей – периоду. Фликкер-щум знаменит своей поразительной универсальностью, он наблюдается в самых различных областях – от флуктуаций удельного сопротивления малых образцов вещества до сейсмической и солнечной активности. Существующие теории фликкер-шума дают его объяснение для малых образцов, но бессильны для крупномасштабных явлений. Дело в том что, в теории пространственный масштаб области генерации фликкер-шума должен покрываться масштабом диффузии. Поэтому для малых масштабов механизм, делающий микрофлуктуации когерентными, понятен. Для крупномасштабных процессов аналогичного механизма не находилось. Вполне вероятно, что им как раз является макроскопическая нелокальность. Интересно, что U/B по размерности пропорционально некоторому удельному сопротивлению, но это шумящее сопротивление мы не можем локализовать!

Далее, оказалось, что U/B² с хорошей точностью от периода не зависит – в соответствии с теоретическим предсказанием. Используя это отношение, удалось оценить сечение взаимодействия s »2×10^–21 м², т.е. порядка сечения атома, как и ожидалось.

Если вместо B в качестве показателя геомагнитной активности взять Dst-индекс, величина опережения главного максимума корреляции с U возрастает до 1–2 месяцев. Уровень корреляции, как правило, становится больше (предпринимая средства по разделению сигналов его удается поднять иногда до 0.70±0.02). Корреляция слабее, чем для синоптической активности, так же как меньше и экстремумы функций независимости и причинности, но качественно картина та же – главные максимумы g и минимумы i_U_÷_Dst наблюдаются в области опережения U относительно Dst. Величина опережения нестабильна, но главные пики укладываются в пределы вышеуказанного диапазона t. Можно сдвинуть реализации и на величину этого t и воочию убедиться в прогностическом эффекте (рис.5).

Рис.5. Вариации сигнала детектора U, прогнозирующие геомагнитную активность Dst c заблаговременностью 33 сут. Начало отсчета времени (в сутках) соответствует 11 января 1997.

Солнечная активность. Солнечная активность – важнейший астрофизический процесс, влияющий на многие земные процессы. В настоящее время глубоко изучены механизмы влияния переменного волнового и корпускулярного излучения Солнца на состояние магнитосферы, ионосферы, магнитного поля, на распространение радиоволн, т.е. на весь комплекс электромагнитных геофизических процессов. Гораздо менее ясен механизм воздействия солнечной активности на нижнюю атмосферу, океан и твердую Землю. Например, установлена связь солнечной и сейсмической активности. Некоторые исследователи, рассматривая механизм этой связи, считают атмосферу промежуточным звеном - солнечная активность вызывает колебания давления, которые и стимулируют землетрясения (а что еще тут можно предложить?). Аналогично, установлена связь темпов накопления некоторых осадочных пород с солнечной активностью. Проще всего было бы это объяснить промежуточными метеорологическими изменениями. Но в том-то и дело, что связь солнечной активности с процессами в нижней атмосфере слаба, неоднозначна и даже до сих пор не признана большинством метеорологов. Многочисленные попытки использовать солнечные данные в прогнозе погоды ни к чему не привели. А с теоретической точки зрения найти механизм влияния солнечных электромагнитных воздействий на гораздо более мощные неэлектромагнитные процессы во всех оболочках Земли ниже ионосферы – задача, по-видимому, обреченная. Другое дело, если существует иной физический механизм связи. Поскольку все такие коррелирующие с солнечной активностью процессы существенно диссипативны, то макроскопическая нелокальность может стать ключом ответа на многие вопросы. Но для начала надо выяснить, присутствует ли в сигналах детекторов составляющая, связанная с солнечной активностью.

В качестве индексов солнечной активности были взяты потоки радиоизлучения Солнца на различных частотах (именно индексов – разумеется, не может быть и речи о прямом влиянии этого радиоизлучения на детектор). Различные частоты соответствуют различным глубинам источников излучения в атмосфере Солнца – чем больше частота, тем глубже. Оказалось, что сигналы детекторов высококоррелированы с потоком солнечного радиоизлучения, причем уровень корреляции закономерно зависит от его частоты. Максимум функции корреляции и минимум функции независимости совпадают и всегда приходятся на частоты 610–2800 МГц. Эта полоса частот соответствует источникам на уровне низов короны – верхов хромосферы. Но это, как известно как раз уровень наибольшей диссипации энергии магнитозвуковых волн в солнечной атмосфере!

Может, однако, возникнуть сомнение: что если связь сигнала детектора с солнечной активностью все-таки локальна, т.е. опосредована каким-то механизмом? Таких механизмов мыслимо два: геомагнитная активность и вариации космических лучей. Но мы уже показали, что связь U с геомагнитной активностью является нелокальной. А версию о космических лучах нетрудно было проверить - благо, космофизическая обсерватория ИЗМИРАН находится всего в 100 м от нашей установки. Оказалось, что связь сигналов нашего детектора с вариациями космических лучей статистически незначима. Таким образом, связь U с солнечной активностью действительно носит прямой характер.

Но, может быть, связь U с солнечной активностью носит все же косвенный характер, т.е. солнечная активность за счет хорошо известных локальных механизмов возбуждает геомагнитную активность, а та уже нелокальным образом коррелирует с U? Такая связь, конечно, есть, поэтому более точный вопрос таков – верна ли теоретическая оценка того, что прямая нелокальная связь сигнала детектора с солнечной активностью преобладает над вышеописанной косвенной? Ответ положительный и его дает нарушение неравенства типа Белла. Чуть забегая вперед, скажем, что вариации U также опережают поток солнечного радиоизлучения (обозначаемый R), запаздывающая корреляция подавлена. Dst связана с R классически и запаздывает относительно него примерно на сутки. Выбираются значения функций независимости в своих главных минимумах при соответствующих сдвигах времени. Локальное воздействие солнечной активности не может миновать магнитосферу, состояние которой характеризует Dst. Т.е. в нашем неравенстве типа Белла Z = R, Y = Dst, X = U. При подстановке вышеупомянутых значений функций независимости (с учетом их погрешностей) оказалось, что неравенство надежно нарушается, т.е. связь R®U прямая нелокальная. Подчеркнем, что речь идет об опережающей связи (а запаздывающая статистически незначима).

Что касается величины опережения, то интересно, что она не единственна. Наблюдается три характерных пика g (минимума i) в диапазоне 42–280 сут., положение двух ближних зависит от частоты R, дальнего (280 сут.) – нет. Относительное смещение этих пиков на разных частотах соответствует диффузии активных областей в солнечной атмосфере снизу вверх. Абсолютный максимум g » 1.6 и абсолютный минимум i_U_÷_R » 0.47 наблюдался для частоты 2800 МГц при t = 42 сут. И сдвинув ряды, получаем наглядное представление о том, что U несет прогностическую информацию о R (рис.6).

Рис.6. Вариация сигнала детектора U, прогнозирующая поток солнечного радиоизлучения R на частоте 2800 Мгц с заблаговременностью 42 сут. Начало отсчета времени соответствует 11 декабря 1996.

Конечно, это не настоящий прогноз – для него надо не просто сдвигать ряды (даже, как у нас, фильтрованные для выделения в сигнале детектора составляющей, обусловленной R, Dst или P). Для настоящего прогноза необходимо рассчитать некоторую весовую функцию сигнала в широком диапазоне t. Это отдельная задача, пока нам важно доказательство самой возможности прогноза!

Во всех описанных случаях эффект макроскопической нелокальности выявлялся в длительных рядах измерений (т.е. с помощью накопления полезного сигнала) с применением современных информационно-статистических методов обработки данных. А можно ли его заметить в отдельных событиях? Мы пытались выявить такого рода индивидуальную связь для различных кратковременных гелиогеофизических процессов, но до 2002г. получили единственный уверенный результат – для внезапных ионосферных возмущений (резких возрастаний электронной концентрации). Но и в этом случае реакция детектора не «индивидуальна» – изменение уровня сигнала соответствует изменению частости (в 4.5±1.1 раз) этих возмущений. Особенно заметен (соответственно, 7.1±0.7 раз) этот эффект для возмущений типа внезапных усилений атмосфериков (свистящих радиосигналов от удаленных гроз), очевидно в связи с тем, что это не чисто ионосферное явление, а связанное с мощными тропосферными процессами. Время опережения здесь особенно размыто, можно говорить лишь о порядке – десятки часов.

2003 год начался с сюрпризов. В период с 1 января по 14 февраля на гладком, как обычно, фоне записи электродного детектора наблюдалось 8 всплесков очень большой амплитуды длительностью около часа. Ничего подобного прежде мы не видели и даже заподозрили, а в порядке ли наша аппаратура? Но с ней все было нормально. Наибольший всплеск (134 мкВ) произошел 3 февраля (рис.7).

Рис.7. Необычный всплеск сигнала детектора U 3 февраля 2003г. (время по Гринвичу).

И именно через 42 дня после него, 17 марта произошла солнечная вспышка класса X (рис.8).

Рис.8. Солнечная вспышка класса X 17 марта 2003г., т.е. 42 суток спустя после показанного на рис. 7 всплеска сигнала детектора (F – интегральный поток рентгеновского излучения).

Вспышки класса X по принятой классификации – наиболее мощные события на Солнце. Соответственно они весьма редки, их может не быть по 10 – 20 лет. Так что нам, наконец, повезло с таким событием. Сопоставление рис.7 и 8 (с учетом типов масштаба) показывает даже явное подобие формы двух кривых. Таким образом, это мощное (и спонтанное – солнечные вспышки непредсказуемы!) явление вызвало опережающую реакцию детектора с несколькими временными сдвигами и с главным всплеском при t =42 сут.

Очень существенно, что несмотря на огромную мощность, эта солнечная вспышка не была геоактивной, т.е. она не вызвала мировой магнитной бури. Дело в том, что хотя поток рентгеновского излучения (рис.8) – очень удобный индекс вспышечной активности, основной механизм возбуждения геомагнитной активности не волновой, а корпускулярный. Плазменный выброс от вспышки распространяется вдоль линий межпланетного магнитного поля и встречается с Землей, только если вспышка произошла в определенном долготном интервале на Солнце. Вспышка 17 марта 2003г. Была как раз вне этого интервала и не вызвала существенных токов в магнитосфере. Следовательно, ее влияние на сигнал детектора было прямым. Сигнал U предварил осенью 2003г. также сопоставимые по мощности вспышки начала ноября, но они были, наоборот, крайне геоактивными, вызвав колоссальную магнитную бурю. Поэтому не эти, а как раз рассмотренное выше событие наиболее показательно.

Логика развития

Геофизика обычно рассматривается как раздел прикладной физики, где мы применяем в конкретных, часто очень сложных условиях законы, полученные в физической лаборатории. Редко, но случается обратное - какие-то явления мы впервые обнаруживаем и изучаем в естественных условиях, а затем в лаборатории. В астрофизике это случается чаще. И именно таково изучение макроскопической нелокальности: странные корреляции практически изолированных геофизических процессов были замечены задолго до того как вопрос о макроскопической нелокальности был поставлен теоретиками.

Несмотря на успешную экспериментальную проверку, вряд ли стоит относиться к предложенной нами математической формулировке гипотезы более серьезно, чем как к эвристическому уравнению. Но она, безусловно, отражает основные черты явления и указывает на необходимость поиска достаточно строгой теории, лежащей на пересечении причинной механики, квантовой нелокальности и теории прямого межчастичного взаимодействия, и на важность продолжения целенаправленных экспериментов.

Уже сейчас ясны возможности и некоторых приложений. Во-первых, открывается перспектива понимания природы большого числа необычных корреляций геофизических и астрофизических процессов. Во-вторых, и это самое интересное, появляется возможность создания метода прогноза гелиогеофизических процессов, принципиально отличающегося от имеющихся тем, что он основан не на экстраполяции их эволюции, а на прямом измерении опережающих сигналов, на, в определенном смысле, наблюдении неконтролируемого будущего как существующей реальности.

Возможно, наше понимание этого круга волнующих проблем еще слишком поверхностно. Мы никогда не узнаем этого, если не двинемся дальше.

Литература

[1] Н.А. Козырев, Избранные труды (Л.: ЛГУ, 1991).

[2] Б.М. Владимирский, Изв. Крымской астрофизической обсерватории, 82, 161 (1990).

[3] С.Э. Шноль, В.А. Коломбет, Э.В. Пожарский, Т.А. Зенченко, А.В. Зверева, А.В. Конрадов, УФН, 168 (10), 1129 (1998).

[4] Н.А. Козырев, В.В. Насонов, Проблемы исследования Вселенной, 7, 168 (1978).

[5] Н.А. Козырев, Проблемы исследования Вселенной, 9, 85 (1980).

[6] Н.А. Козырев, В.В. Насонов, Проблемы исследования Вселенной, 9, 76 (1980).

[7] D. Savage, in Progress in Space-Time Physics, edited by B.Wesely (Blumberg, 1987), p.242.

[8] М.М. Лаврентьев, И.А. Еганова, В.Г. Медведев, В.К. Олейник, С.Ф. Фоминых, ДАН, 323 (4), 649 (1992).

[9] A.C. Elitzur and S. Dolev, in The Nature of Time: Geometry, Physics and Perception, edited by R. Bucceri (Kluwer Academic Publishers, 2003), p.297.

[10] D. Home and A.S. Majumdar, Phys. Rev. A, 52, 4959 (1995).

[11] А.М. Башаров, ЖЭТФ, 121, 1249 (2002).

[12] J.G. Cramer, Phys. Rev. D, 22, (1980).

[13] F. Hoyle and J.V. Narlikar, Rev. Mod. Phys., 67, 113 (1995).

[14] S.M. Korotaev, Galilean Electrodynamics, 4 (5), 86 (1993).

[15] С.М. Коротаев, Геомагнетизм и аэрономия, 32 (5), 27 (1992).

[16] О.А. Хачай, С.М. Коротаев, А.К. Троянов, Вулканология и сейсмология, 3, 92 (1992).

[17] Физика Земли, 6, 77 (1992).

[18] С.М. Коротаев, О.А. Хачай, С.В. Шабелянский, Геомагнетизм и аэрономия, 33 (2), 128 (1993).

[19] С.М. Коротаев, Геомагнетизм и аэрономия, 35 (3), 116 (1995).

[20] С.М. Коротаев, М.О. Сорокин, В.О. Сердюк, Ю.М. Абрамов, Физическая мысль России, 2, 1 (1998).

[21] С.К. Дворук, С.М. Коротаев, А.Н. Морозов, А.Л. Назолин, В.О. Сердюк, А.В. Соловьев, М.О. Сорокин, С.Е. Табалин, Г.В. Шишкин, Прикладная механика и технологии машиностроения, 1 (4), 61 (1998).

[22] С.М. Коротаев, М.О. Сорокин, В.О. Сердюк, Ю.М. Абрамов, Наука и технология в России, 1, 16 (1999).

[23] S.M. Korotaev, V.O. Serdyuk, M.O. Sorokin and J.M. Abramov, Phys. Chem. Earth A, 24 (8), 735 (1999).

[24] S.M. Korotaev, V.O. Serdyuk, and M.O. Sorokin, Galilean Electrodynamics, 11 (2), 23 (2000).

[25] С.М. Коротаев, В.О. Сердюк, М.О. Сорокин, Геомагнетизм и аэрономия, 40 (3), 56 (2000).

[26] С.М. Коротаев, А.Н. Морозов, В.О. Сердюк, М.О. Сорокин, Известия высших учебных заведений. Физика, 5, 3 (2002).

[27] S.M. Korotaev, A.N. Morozov, V.O. Serdyuk, and J.V. Gorohov, in Physical Interpretation of Relativity Theory, edited by M.C.Duffy (Moscow: BMSTU Press), p.200.

[28] С.М. Коротаев, А.Н. Морозов, Ю.В. Горохов, В.И. Наливайко, А.Н. Новыш, С.А. Пулинец, В.О. Сердюк, в: Необратимые процессы в природе и технике. Труды второй всероссийской конференции (М.: МГТУ, 2003), с.12.

[29] S.M. Korotaev, V.O. Serdyuk, V.I. Nalivaiko, A.V. Novysh, S.P. Gaidash, Yu.V. Gorokhov, S.A. Pulinets and Kh.D. Kanonidi, Phys. Wave Phenomena, 11 (1), 46 (2003).

[30] С.М. Коротаев, В.О. Сердюк, В.И. Наливайко, А.Н. Новыш, С.П. Гайдаш, Ю.В. Горохов, С.А. Пулинец, Х.Д. Канониди, в: Исследования в области геофизики, ред. А.О. Глико (М.: ОИФЗ, 2004), с.167.

[31] S.M. Korotaev, V.O. Serdyuk, J.V. Gorohov, S.A. Pulinets and V.A. Machinin, Frontier Perspectives, 13 (1), 42 (2004).

[32] С.М. Коротаев, В.О. Сердюк, М.О. Сорокин, В.А. Мачинин, Физическая мысль России, 3, 20 (2000).

[33] С.М. Коротаев, В.О. Сердюк, М.О. Сорокин, В.А. Мачинин, Вестник ОГГГГН РАН, 4, 106 (2000).