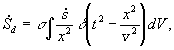 (1)
(1)Известия высших учебных заведений. Физика. 2002. № 5. С. 3-14.
© С.М.Коротаев, А.Н.Морозов, В.О.Сердюк, М.О.Сорокин
УДК 530.1 + 550.34.01 + 551.436.7
Проявление макроскопической нелокальности в некоторых естественных диссипативных процессах
С.М. Коротаев, А.Н. Морозов, В.О. Сердюк, М.О. Сорокин
Поставлен эксперимент по проверке гипотезы макроскопической нелокальности диссипативных процессов, синтезирующей принципы квантовой нелокальности и теории прямого межчастичного взаимодействия. Нелокальное взаимодействие выражается через связь производства энтропии в любых диссипативных процессах. Сконструировано три типа детекторов этого взаимодействия. Выполнен длительный эксперимент по измерению реакции детекторов на различные естественные процессы - вариации температуры, магнитного поля, внезапные ионосферные возмущения и солнечную активность. Доказан нелокальный характер этой реакции. Важной ее чертой оказалось наличие опережающего временного лага.
Введение
В последние годы появились теоретические соображения о сохранение эффекта квантовой нелокальности в сильном макропределе (хотя идея экспериментальной проверки этого заключения не была предложена) [1-3]. Интерпретация квантовой нелокальности в рамках теории прямого межчастичного взаимодействия Уилера-Фейнмана [4] в ее современной трактовке [5] позволило предположить, что на макроуровне нелокальность проявляет себя как связь производств энтропии в практически изолированных процессах. Вытекающая отсюда идея экспериментальной проверки была независимо реализована в Институте геомагнитных исследований РАН (ИГЭМИ) и в Центре прикладной физики МГТУ им. Н.Э.Баумана (ЦПФ) [6-10]. Хотя вполне вероятно, что эффект макроскопической нелокальности уже наблюдался в рамках ранних экспериментов по причинной механике, уровень строгости их был невысок для ответственных выводов [11-20]. Эксперименты на установках ИГЭМИ и ЦПФ, выполненные на современном уровне строгости (начиная с постановки задачи и кончая ее технической реализацией), позволили сделать позитивное заключение о наличии эффекта макроскопической нелокальности и изучить некоторые его свойства.
В работах [6-10] приведены предварительные результаты долговременного эксперимента по изучению эффекта нелокальности крупномасштабных естественных процессов. В настоящей статье описываются окончательные результаты этого эксперимента.
1. Формулировка проверяемой гипотезы
В [6,8] предложен следующий вид уравнения макроскопической нелокальности (без учета поглощения промежуточными средами):
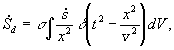 (1)
(1)
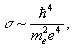 (2)
(2)
где
d -функция в (1) показывает наличие наряду с обычной запаздывающей, симметричной по времени опережающей корреляции. Согласно [4] это не нарушает принцип слабой причинности если источник является неконтролируемым наблюдателем процессом. Если источник контролируется наблюдателем, то выполняется принцип сильной причинности и наблюдается только запаздывающая корреляция [4]. Поэтому особый интерес представляет постановка эксперимента в котором процессом-источником были бы неконтролируемые (естественные) процессы.
Одним из положений теории Уилера-Фейнмана является полное поглощение поля веществом. Однако в современной трактовке теории показано [3], что это касается только запаздывающей части поля, поглощение же опережающей части, напротив, обязано быть неполным. Следовательно, экранирующие свойства вещества по отношению к опережающему полю должны быть ослаблены [6]. Поэтому наличие между неконтролируемым источником и детектором промежуточных сред должно приводить к большей амплитуде опережающей реакции детектора относительно запаздывающей. Наконец заметим, что если взаимодействие происходит через среду с участием диффузионных процессов (т.е. проходит по межчастичным цепям через микроскопические электромагнитные поля Уилера-Фейнмана), то величины результирующего запаздывания и опережения будут велики.
2. Постановка экспериментальной задачи
Задача эксперимента – обнаружение связи изменения энтропии в некотором пробном процессе с изменением энтропии в естественных (геофизических и гелиофизических) процессах в соответствии с (1) при исключении всех известных видов классического локального взаимодействия. Если же такое исключение невозможно, необходимо применение того или иного математического теста присутствия нелокальности. Хотя в качестве пробного процесса в детекторе может использоваться любой диссипативный процесс, непосредственно измеряется не энтропия, а та или иная косвенно связанная с ней наблюдаемая величина, поэтому вопрос о выборе типа детектора решается из ожидаемой величины относительного эффекта. По этому критерию нами избраны три типа детекторов. В установке ИГЭМИ использовались детектор, основанный на измерении собственных потенциалов слабополяризующихся электродов в электролите, и детектор, основанный на измерении темнового тока фотоумножителя. В установке ЦПФ использовался детектор, основанный на регистрации флуктуаций подвижности ионов в малом объеме электролита [21].
Как показал эксперимент, первый тип детектора оказался в контексте данного эксперимента более удачным, поэтому именно его данные в наибольшей степени использовались для количественной интерпретации. Полная теория электродного детектора приведена в [6]. Хотя точные выражения, связывающие энтропию в двойном электрическом слое Sd (пробный процесс) с разностью собственных потенциалов электродов U (сигнал детектора), весьма громоздки, в хорошем приближении их связь описывается простым соотношением![]() (3)
(3)
где
q - заряд ионов жидкой фазы, g - эффективность детектора, средней мерой которой является коэффициент вариации.При постановке эксперимента должны быть исключены или стабилизированы все известные локальные факторы, воздействующие на величину
U: температура, давление, химизм, концентрация или движение электролита, освещенность, эффект старения электрода, электрическое поле. Помимо внешней экранировки от перечисленных помехообразующих факторов, их воздействие минимизируется при измерениях с практически нулевой базой, когда электроды сближены на минимальное конструктивно допустимое расстояние (порядка сантиметра). В таком варианте любое аддитивное воздействие в U исключается, и остается лишь мультипликативное. Поэтому даже при больших изменениях потенциалов знак U не меняется и может быть фиксирован как положительный, а сама по себе величина U несущественна для относительной меры эффекта. Качественно это означает, что согласно (3) ожидается, что воздействие внешних процессов с положительным производством энтропии влечет понижение U.Для детектора на основе фотоумножителя аналогом
U является работа выхода. Помехообразующими факторами, подлежащими исключению или контролю, являются: температура, электрическое и магнитное поле, освещенность, влажность, нестабильность питающего напряжения.Для детектора, принцип действия которого основан на регистрации флуктуации подвижности ионов, энтропия линейно связана с дисперсией флуктуаций тока, текущего через небольшой объем электролита. В качестве мешающих факторов выступают: температура, электромагнитные наводки, электрохимические реакции.
3. Выполнение эксперимента
Установка ИГЭМИ включала два типа детекторов предполагаемого взаимодействия и аппаратуру для сопровождающих измерений.
Детектор на основе слабополяризующихся электродов построен следующим образом. В качестве электродов избраны геофизические графитомарганцевые электроды типа "ИЗМИРАН - Севморгео". Этот тип отличается малым температурным и барическим коэффициентом и отсутствием зависимости потенциала от концентрации ионов (
Na+Cl-). Электроды до начала эксперимента 9 лет выдерживались в поднасыщенном водном растворе NaCl, и этот же раствор использован в эксперименте в качестве электролита. Это позволило исключить влияние эффекта старения и переходных диффузионных процессов. Хорошо проводящий электролит играет также роль экрана от внешнего электрического поля.Схема устройства электродного детектора показана на рис. 1. Электроды помещаются изолирующими корпусами вплотную друг к другу в стеклянном сосуде с электролитом, так что расстояние между контактными окнами составляет 1,5 см. Минимальная межэлектродная база, однородность электролита и материал сосуда исключают эффект внутреннего электрического поля. Сосуд жестко герметизирован, так что полностью исключается как испарение, так и передача колебаний атмосферного давления на электроды. Сосуд помещается в дьюар, покрытый снаружи дополнительными слоями световой и термической изоляции. Максимум корреляции внешней (лабораторной) и внутренней температур ~0,6 наблюдается при запаздывании последней на 11,5 ч. Для контроля остаточных вариаций температуры между внутренней стенкой дьюара и сосудом с электродами помещен термодатчик, позволяющий непрерывно измерять их с точностью до 0,001К. Входное сопротивление измерительного усилителя равно 50 МОм. Таким образом, исключалось влияние всех помехообразующих факторов, кроме температуры. Влияние вариаций последней было минимизировано и контролировалось. Величина
U непрерывно измерялась с точностью до 0,5 мкВ.Второй тип детектора построен на основе фотоумножителя ФЭУ-64 с сурьмьяно-цезиевым катодом малой площади, избранного по признаку временной стабильности. Фотоумножитель помещен в дьюар, окруженный снаружи заземленным медным экраном, слоями световой и дополнительной термической изоляции. Между внутренней стенкой дьюара и ФЭУ также помещался термодатчик, позволяющий непрерывно регистрировать остаточные вариации температуры с точностью до 0,0009 К. Устройство фотокатодного детектора, таким образом, аналогично электродному – сосуд с электродами заменен в нем экранированным ФЭУ. Делитель динодного напряжения и нагрузочное анодное напряжение смонтированы на панели ФЭУ и находились внутри дьюара. Использована двойная стабилизация питающего напряжения, составляющего 1500 В, с относительной погрешностью не более 10
-3. Для повышения надежности это напряжение также находилось под непрерывным контролем. ФЭУ был включен в рабочий режим задолго до начала эксперимента для исключения влияния усталостных процессов. Таким образом исключались все помехообразующие факторы кроме температуры, влияние которой было минимизировано и контролировалось, а также магнитного поля. Влияние естественного магнитного поля на работу ФЭУ считается пренебрежимо малым для любых реально наблюдаемых амплитуд (<0,1 А/м). Тем не менее, возможное влияние магнитного поля контролировалось квантовым модульным магнитометром КМ-2м с точностью до 8· 10-6 А/м. Датчик магнитометра помещался в непосредственной близости (1,5м) от детектора для учета, кроме естественных, возможных техногенных магнитных полей. Темновой ток I непрерывно измерялся с точностью до 0,05 нА.Измерения магнитного поля служили также индикатором одного из геофизических процессов – диссипации ионосферных токов. Наконец, непрерывно регистрировалась общая температура воздуха в лаборатории с точностью до 0,1К. Таким образом, измерения на установке включали 2 основных канала и 4 вспомогательных.
По стечению обстоятельств, в течение части срока нашего эксперимента и совершенно независимо, измерения собственных потенциалов электродов в других целях выполнялись В.И. Наливайко, любезно предоставившего нам свои материалы. Им использованы геофизические электроды другого типа – серебряные-хлорсеребряные ХД-5.519.00 в
NaCl электролите. Его установка не предусматривала измерений каких-либо помехообразующих факторов, кроме самой величины U, и специальных мер защиты от них, в том числе вариаций температуры и давления (фактически исключалось только влияние освещенности), между электродами имелась конечная база ~ 50 см. Тем не менее, если полезный сигнал, связанный с крупномасштабными естественными процессами, в вариациях U достаточно велик, то, учитывая небольшое расстояние между лабораториями (300 м), можно было рассчитывать на корреляцию с нашими измерениями. Поэтому измерения В.И. Наливайко вошли как седьмой канал в набор обрабатываемых данных.Измерения на установке ИГЭМИ выполнялись в непрерывном режиме с 10 декабря 1996 г. по 11 декабря 1997 г.
В установке ЦПФ в качестве детектора использовалась электролитическая ячейка, разделенная на два сосуда с помощью лавсановой пленки толщиной 6 мкм, имеющей отверстия диаметром 0,2...0,4 мкм [21]. В каждом из сосудов размещалось по графитовому электроду, которые обеспечивали подвод электрического тока к электролиту. Схема детектора показана на рис.2. Электролитом являлся слабый раствор серной кислоты. Сопротивление электролитической ячейки определялось величиной отверстий в лавсановой пленке и равнялось примерно 50 кОм. При приложении внешнего напряжения величиной 1...2 В через электролит, находящийся в отверстиях пленки, протекал электрический ток, флуктуации которого вызывались случайными изменениями подвижности ионов в электролите. Возникающие при этом флуктуации напряжения на электролитической ячейке усиливались в полосе 5...15 кГц и с частотой опроса 60 кГц считывались в ПЭВМ. Возведенные в квадрат значения флуктуаций напряжения усреднялись за период времени равный одной минуте и записывались в долговременную память ПЭВМ. Указанная процедура обработки сигнала обеспечивала регистрацию низкопериодных изменений дисперсии флуктуаций напряжения
b на электролитической ячейке, что позволяло исследовать влияние внешних процессов на характер флуктуаций подвижности ионов в электролите.Для подавления возможных мешающих факторов детектор был размещен в подвальном помещении, термически изолирован и экранирован от электромагнитных наводок. С целью устранения влияния атмосферного давления и испарения электролита сосуды электролитической ячейки герметизировались.
Одновременно с записью сигнала с детектора выполнялась со скважностью в одну минуту регистрация наружной атмосферной температуры
Ta. Измерения на установке ЦПФ осуществлялись непрерывно с 17 января по 19 сентября 1997 года.4. Обработка данных
Помимо перечисленных выше данных измерений, в обработку включались стандартные международные данные по ионосферной и солнечной активности.
Данные обрабатывались методами корреляционного, регрессионного, спектрального и причинного анализа. Последний следует отметить особо, ввиду его адекватности теории рассматриваемого эффекта [22]. Существо метода состоит в следующем. Для произвольных наблюдаемых Х и
Y через условные и безусловные шенноновские энтропии Н могут быть введены функции независимости i:![]()
Например: если
Y — однозначная функция X, то iY|X=0, если Y не зависит от X, то iY|X=1. Далее рассматривается функция причинности![]()
и определяется, что если
g<1, то X – причина, Y – следствие. Если g >1, то X – следствие, Y – причина.Случай
g=1 означает адиабатическую (непричинную) связь X и Y. На теоретических и многочисленных экспериментальных примерах ([23-26] и др.), было показано, что такое формальное определение причинности не противоречит интуитивному пониманию в очевидных ситуациях и может быть использовано в неочевидных. На этом основан метод причинного анализа, позволяющий количественно оценивать параметры причинности как пары, так и множества наблюдаемых.Аналогом корреляционной функции в причинном анализе являются функции
1-i, но в отличие от первой они в равной степени пригодны для линейных и любых нелинейных типов зависимости. Поскольку аппарат причинного анализа равно пригоден для любого распределения вероятностей (эмпирические распределения всех изучаемых величин оказались существенно негауссовыми), приводимые в разделе 5 оценки погрешностей i и g, получены не стандартным вероятностным методом, а определяются как ошибка от поочередного зашумления сравниваемых временных рядов 21% (по мощности) фликкер-шумом. Фликкер-шум избран как наиболее естественная модель как природных, так и аппаратурных низкочастотных шумов. Шум синтезируется во временной области из полного набора фурье-гармоник с распределением энергий по закону 1/f и с общей нулевой начальной фазой. Последнее необходимо для максимизации влияния шума при заданном уровне интегральной мощности, на эмпирическое распределение вероятностей сигнала. Фактически, таким образом получаются оценки устойчивости расчетных параметров. При заданном уровне шума это означает требование i/|di|>10, g/|dg|>10. Все приводимые в разделе 5 результаты отвечают этим критериям.Преимуществом корреляционного анализа перед причинным является только возможность простого перехода к регрессии. Кроме того, при высокой корреляции корреляционная функция сдвига времени
r(t) имеет более гладкий вид и более наглядна, чем i(t). Каждая оценка корреляции и других стандартных статистических параметров, приводимых в разделе 5, сопровождается оценкой вероятной погрешности. Корреляция считается значимой, если, согласно критерию Визе, |r/dr|>10. Этот критерий значимости имеет надежность заведомо больше 0,999 даже для существенно негауссовых распределений.В спектральном представлении интерес представлял не столько поиск скрытой периодичности, сколько оценки амплитуд, поэтому избран метод оценки спектров интегралом Фурье с предварительным снятием тренда, аппроксимируемого кубическим полиномом.
Хотя аппаратура обеспечивала скважность измерений по всем каналам не хуже 1 минуты, обработка показала, что значимые амплитуды наблюдаемых начинаются с периодов порядка часов и более. Поэтому статистической интерпретации подвергались временные ряды с дискретностью 30 минут. Объем выборки по каналам установки ИГЭМИ составил, таким образом,
N=17569 отсчетов. Несколько меньше объем выборки для установки ЦПФ (п. 5.1.): N=11809, и для удаленного детектора (п. 5.2.): N=11209.В тех случаях, когда описываемые в разделе 5 статистические результаты не соответствуют вышеприведенным критериям значимости, это отмечается особо. В случаях сравнения уровней корреляции надежность вывода принята не менее 0,99, при меньшем значении это также особо оговаривается.
5. Результаты эксперимента и их интерпретация
Как показывается ниже, результаты измерений на всех трех типах детекторов оказались достаточно коррелированными. Однако уровень техногенных помех для установки ИГЭМИ, расположенной в Троицке (ИЗМИРАН) многократно ниже, чем для установки ЦПФ, расположенной в Москве. В свою очередь, из двух типов детекторов установки ИГЭМИ связь сигнала с изучаемыми внешними факторами оказалась заметно более устойчивой для электродного детектора. Поэтому основное внимание далее будет уделено результатам, полученным именно с этим детектором.
5.1. Связь вариаций на установках ИГЭМИ и ЦПФ.
Сравнение сигналов на удаленных на 40 км установках ИГЭМИ и ЦПФ сразу позволяет установить, не являются ли их вариации чисто внутренними шумами. Коэффициент корреляции
U (ИГЭМИ) и b (ЦПФ) по всему выполненному ряду наблюдений равен 0,7155.2. Связь потенциалов на разнесенных установках.
Аналогичный смысл имеет корреляция
U на установке ИГЭМИ и упомянутой в разделе 4 удаленной на 300 м установке Ur. Коэффициент корреляции U и Ur оказался равен 0,68Коэффициент частной корреляции при устранении изменений, вызванных влиянием внутренней температуры
TU детектора U оказался равным 0,74 ± 0,01 — выше, чем коэффициент простой парной корреляции. Следовательно, локальное влияние температуры не является общей причиной коррелирующих вариаций потенциалов. Такой общей причиной остается считать нетривиальное воздействие внешних геофизических процессов.5.3. Связь потенциалов с внутренней и внешней температурами.
Благодаря пассивному термостатированию, дисперсия вариаций внутренней температуры
TU воздуха в дьюаре детектора U очень мала (снижена на два порядка относительно внешней лабораторной температуры Te). Поэтому имеется лишь небольшой пик корреляцииДля коротких возмущений
U их опережение относительно TU можно заметить без всякой обработки, непосредственно в регистрограммах (рис.3).Обратимся теперь к анализу связи
U с внешней температурой Te. Поскольку внутри дьюара, где измеряется TU, нет источников тепла, то локальная связь вариаций потенциалов с температурой осуществляется по причинной цепи Te®TU®U. Это накладывает ограничения на независимости [24]:![]() . (4)
. (4)
Нарушение соотношений (4) является достаточным признаком нелокальности взаимодействия
Te и U. Это вполне подобно нарушению неравенств типа неравенства Белла в квантовой нелокальности. Оказалось, что i(t) имеет три почти симметричных минимума при t=0 и ±27,0 ч. Этот результат (за исключением порядка скорости передачи сигнала) в точности соответствует результату известного астрофизического эксперимента [12]. Асимметрия сводится к более сильной опережающей связи по сравнению с запаздывающей (как и для описанной выше связи U с TU): при t=-27.0 чРассмотрим теперь изменения атмосферной температуры Та как пример крупномасштабного геофизического процесса. Учитывая пассивное термостатирование, локальная причинная связь Та
®Те® TU® U должна приводить к слабой корреляции U c Ta с весьма большим (многосуточным) запаздыванием. Следуя обычной геофизической практике изучения крупномасштабных процессов, для исключения возможного влияния мелкомасштабных неоднородностей, сравним измерения U c Ta в удаленных точках. При характерном горизонтальном синоптическом масштабе сотни км, разнос между установками ИГЭМИ и ЦПФ 40 км вполне оптимален. Поэтому для сравнения с U были взяты измерения наружной температуры воздуха Та вблизи установки ЦПФ. На рис.4 представлена корреляция U и Та. Важнейшая ее черта – резкое превышение корреляции при опережении U относительно Та (t>0) над запаздывающей корреляцией (t<0). Далее, наблюдаются пять максимумовЭнтропия окружающей среды примерно логарифмически связана с температурой [28]. Однако количественно установить эту связь, учитывая процессы в атмосфере и подстилающей твердой Земле, крайне затруднительно. В этом смысле производство энтропии в электромагнитных процессах, рассматриваемое ниже, гораздо удобнее.
5.4. Связь потенциалов с геомагнитными вариациями.
Нет никаких оснований считать, что
U каким-то образом зависит от напряженности магнитного поля F. Поэтому хорошим тестом для гипотезы (1) было бы обнаружение связи потенциалов с естественными вариациями магнитного поля Земли, поскольку эти вариации легко могут быть связаны с омической диссипацией в их источнике.Для того чтобы иметь полную уверенность в отсутствии прямого влияния
F на U, были проведены опыты по воздействию на детектор U искусственного постоянного и переменного (частотой до 1 Гц) магнитного поля величиной до 100 А/м. В пределах чувствительности детектора (0,5 мкВ) какое-либо влияние отсутствовало.Анализ естественных вариаций показал наличие корреляции
rUF=-0,56±0,01 с большим (t=48 ч) опережением U относительно F. В области запаздывания U (t<0) значимая корреляция отсутствует. В причинном анализе практически при том же t=48,5 ч наблюдается минимум независимости iF|U=0,79Итак, связь естественных вариаций
U и F статистически достоверна. Но, как из априорных соображений, так и благодаря опережению U относительно F, она не может быть результатом прямого воздействия магнитного поля на детектор. Следовательно, F является лишь индикатором некоторого процесса, воздействующего на U.Анализ амплитудных спектров показал, что по крайней мере в диапазоне периодов
t от 5 часов до 10 суток (с наименьшим отношением сигнал/шум), хотя U(f)/F(f) зависит от частоты f, U(f)/F2(f) от частоты не зависит: U(f)/F2(f)=(1,7±0,2)·10-5Ом·м2/A.Для интерпретации рассмотрим приложение (1) к конкретной ситуации. Магнитное поле
F связано с токами, текущими в источнике - ионосфере, а также с индуцированными токами в подстилающей Земле. Для упрощения задачи пренебрежем последними и рассмотрим производство энтропии в процессе омической диссипации только в источнике поля F. Удельное производство энтропии легко выразить через гармоническое электрическое поле E(f) (которое, в свою очередь, через импеданс Z(f) связано с F(f)), удельное сопротивление r и температуру среды T. r и Z(f) будем для простоты считать скалярными. Тогда: . (5)
. (5)
Комбинируя (1), (3) и (5) в приближении плоской волны имеем:
![]() (6)
(6)
Таким образом, экспериментальный факт постоянства
U(f)/F2(f) объясняется в рамках гипотезы (1).Интересно оценить из наблюдений константу
s. Для этого еще немного упростим (6), считая, что, подобно обычному электромагнитному полю ионосферного источника, можно применить приближение плоской волны. Тогда (6) переходит в![]() , (7)
, (7)
где
h — толщина динамо-слоя. Для оценки s примем соответствующие детектору параметры TU=3·102K, g=6·10-2, q=1,6·10-19 A·c, и известные характерные значения ионосферных параметров Т=103К, h=5·104м. Тогда при полученном в эксперименте значении U(f)/F2(f)=1,7·10-5Ом·м2/A, получаем из (7) s=2·10-21м2, что согласуется до первого знака с (2). Разумеется, это сугубо предварительная порядковая оценка. Для ее уточнения нужна более совершенная модель источника.5.5.Связь потенциалов с ионосферной активностью.
Обнаружено, что вероятность внезапных ионосферных возмущений на фазе роста
U значительно превышает эту вероятность на фазе падения. Отношение вероятностей равно 4.5. Если же из всех типов ионосферных возмущений выделить внезапное усиление атмосфериков, то отношение вероятностей на фазе роста и падения становится 7.1.Можно предположить следующую качественную интерпретацию этих фактов. Внезапные ионосферные возмущения — это резкое возрастание ионизации нижней ионосферы. Ему соответствует уменьшение энтропии, влекущее, согласно (1) и (3), увеличение разности потенциалов. Больший эффект от внезапных усилений атмосфериков вызван тем, что они не представляют в чистом виде ионосферное явление, а связаны также с усилениями грозовой активности.
5.6.Связь потенциалов с солнечной активностью.
Спектральный анализ обнаружил цикличность изменений
U с солнечным синодическим периодом 27 суток и амплитудой ~1 мВ. Это подтверждает результат близкого по технике постановки эксперимента по измерению контактной разности потенциалов металл-полупроводник [29].Анализ во временной области дает более детальную информацию. Поскольку опыт солнечно-земной физики показывает, что зависимость любых процессов от солнечной активности растет с масштабом временного осреднения, данные обрабатывались с суточным и месячным осреднением. Первые обрабатывались методами причинного и корреляционного анализа, вторые – только корреляционного (поскольку причинный анализ требует большей статистики).
Рассмотрим суточно-осредненные данные. На рис.5 показаны синхронные функции независимости
U от потока солнечного радиоизлучения R (в стандартном диапазоне 245 … 15400 МГц) и их корреляционная функция. Обе кривые указывают оптимальную частоту 1415 МГц, соответствующую излучению из нижней короны - верхней хромосферы, т.е. как раз из слоя наиболее интенсивных диссипативных процессов. На этой частотеМожно, однако, предположить, что все же имеется один локальный механизм влияния солнечной активности на детектор – вариации потока космических лучей. Мы проверили это по данным нейтронного монитора ИЗМИРАН, расположенного вблизи (10
0 м) от установки ИГЭМИ. Корреляция U с потоком космических лучей оказалась значительно слабее: -0,30± 0,03 при суточном осреднении и не значима при месячном осреднении. Следовательно, космические лучи не являются носителями взаимодействия.Максимум зависимости
U от R (соответствующий minМесячно-осредненные данные демонстрируют эту опережающую связь даже более выразительно. На рис.6 представлены эти данные
U и R, сдвинутые на 1 месяц. Сильная корреляция очевидна. При t=1 мес rUR=0,76± 0,08. При симметричном t=-1 мес корреляция не значима.5.7. Связь сигналов на двух детекторах установки ИГЭМИ.
На детекторе темнового тока
I обнаружены те же геофизические эффекты, что и на детекторе U, хотя выражены они слабее; I существенно коррелирует с U. Однако, в отличие от случаев связи различных удаленных процессов, рассмотренных в пп. 5.1 и 5.2, обнаружение корреляции U и I само по себе недостаточно, поскольку имеется возможность тривиальной локальной связи через общий фактор – лабораторную температуру Те.На рис.7 показаны синхронные спектры
I, U, Te. Видно хорошее подобие спектров I и U (в частности, совпадение амплитудных максимумов на периодах 28,2 ч и 16,6 ч). Напротив, спектр Te совершенно иной. Например, период главного низкочастотного максимума Те равный 60 ч, соответственно в 1,6 и 2,0 раза короче периодов главных максимумов I и U. Уже отсюда очевидно, что связь вариаций U и I не может тривиальным образом объясняться воздействием общей причины – вариациями Те.Рассмотрим значения набора всех синхронных простых парных и частных корреляций тройки
U, I, Te:
Частная корреляция
UI несколько выше простой (надежность 0.95), частная корреляция UTe вдвое ниже простой, а частная корреляция ITe отсутствует. Значения корреляций говорят о том, что связь U c Te втрое слабее, чем с I, а прямая связь I c Te практически отсутствует; конечное значениеОсобенностью
I как индикатора естественных диссипативных процессов является то, что в некоторых случаях стандартные отклонения I демонстрируют более выразительную связь с ними, чем средние I . На рис.8 показаны амплитудные спектры посуточного стандартного отклонения I и среднесуточного потока радиоизлучения R. Левый пик амплитуд имеет период 27 сут (синодический период вращения Солнца).Заключение
Результаты долговременного эксперимента, выполненного на приемлемом уровне строгости, позволяют сделать позитивное заключение о существовании нелокального взаимодействия диссипативных процессов. Тот факт, что эвристическая формулировка гипотезы, оказалась обладающей верифицированной предсказательной способностью, заставляет считать актуальной более глубокую разработку теории, лежащей на пересечении идей квантовой нелокальности, теории прямого межчастичного взаимодействия и причинной механики.
Характерной чертой нелокального взаимодействия естественных (неконтролируемых) процессов является наличие опережающего временного лага. Это позволяет на основе описанной техники развить принципиально новый метод прогноза диссипативных процессов такого рода.
В самое последнее время на модифицированной установке ИГЭМИ удалось также выполнить эксперимент по изучению эффекта макроскопической нелокальности искусственных контролируемых процессов-источников [30]. Этот эксперимент подтвердил основные черты макроскопической нелокальности, описанные выше, в рамках наблюдений только запаздывающего сигнала. Новым результатом явилось обнаружение стохастичности реакции пробного процесса на строго фиксированный по всем параметрам процесс-источник (процесс фазового перехода жидкость-газ). Стохастический характер реакции детектора позволяет считать конечность приведенных в п.5 корреляционных функций и функций независимости не только результатом множественности естественных процессов-источников, но и следствием квантомеханической основы эффекта нелокальности.
Настоящая работа завершена при поддержке Российского фонда фундаментальных исследований и правительства Московской области (грант 01-05-97015).
Литература