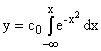 , (2.2)
, (2.2)ГЛАВА 2. БИОЛОГИЯ
КОНЦЕПЦИЯ ОРГАНИЧЕСКОГО ВРЕМЕНИ Г.БАКМАНА И ОПЫТ ЕЕ ПРИМЕНЕНИЯ
§1. Общие положения
Среди многочисленных поисков конструктивных решений проблемы содержательного анализа и формализации собственного времени биологических систем своей конструктивностью выделяется концепция органического времени Гастона Бакмана (1883—1964). Проблемой времени он занимался в связи с разрабатываемой им общей теорией роста животных организмов. Для этого он вел обширные исследования процесса роста у людей, растений, высших и низших животных. Первую работу такого направления Г.Бакман опубликовал в трудах Латвийского университета (Backman, 1925), где он работал на медицинском факультете по приглашению с 1920 по 1925 г., организовал здесь кафедру анатомии и анатомический музей. Итоги своих многолетних исследований он подвел в книге “Рост и органическое время” (Backman, 1943), будучи директором института анатомии Лундского университета в Швейцарии. В послесловии этой книги читаем: “Рост лежит в корне жизни
и является надежным выражением самой внутренней сущности жизни (...). Возможность предсказания событий течения жизни из роста заключается в знании того, что организмы обладают своим “собственным временем”, которое я обозначаю как их “органическое время”” (Backman, 1943, с.177—178).Свой теоретико-методический подход Г.Бакман строит как на индуктивной, так и дедуктивной основе. Теоретические постулаты он конкретизирует в форме математических моделей и для проверки их адекватности использует сборные экспериментальные данные по росту организмов целого ряда классов многоклеточных. Проанализировав известные формулы роста организмов (Ферхольста, Гомпертса, Поттер — Броди, Бастиена и Генри, Тейсира, Хеслина и др.), Г.Бакман выявляет их недостаточную адекватность.
Так, симметричная S-образная кривая, которой обычно аппроксимировали рост организмов, не отражает характерную особенность их роста. Эта особенность заключается в том, что период снижения скорости роста обычно более длителен, чем период ее возрастания. Поэтому половины своих конечных размеров организм достигает после наступления максимума прироста, но еще до середины общей продолжительности своей индивидуальной жизни. Это явление Г.Бакман объясняет тем, что биологическое движение имеет логарифмический характер. Собственное время биологических явлений при этом понимается как логарифмическая функция физического времени. Кривая роста организма, построенная по такому органическому времени, получается симметричной.Г.Бакман, вслед за Т.Робертсоном, выделяет три цикла роста многоклеточных организмов: овулярный, примордиальный (эмбриональный) и инфантильный (основного роста), у млекопитающих добавляется еще цикл половой зрелости, накладывающийся на часть основного роста. Второй цикл не завершается в момент рождения или прорастания семени, а продолжается еще некоторое время, перекрываясь с уже начавшимся третьим циклом. У одноклеточных наблюдается лишь первый цикл роста — большой овулярный период. У более развитых вольвоксовых (колониальные формы) к этому циклу присоединяется второй цикл — большой эмбриональный (примордиальный) период. В процессе дальнейшей эволюции появляется третий цикл, который начинает занимать все больший период онтогенеза (у растений — 75 — 85%, у животных — 90 — 95%, у человека — около 99%). Каждому циклу свойствен свой характерный темп органического времени, и поэтому таковой должен определяться отдельно. Сопоставлять органическое время организмов разных видов (или популяций) и ступени их возраста, используя выведенные Г.Бакманом формулы, также следует лишь по соответствующим циклам роста.
§2. Функция органического времени
Исходной информацией для функции Г.Бакмана служат количественные значения процесса роста организмов (рост в длину, увеличение массы и др.). Он обосновывает достаточность такой информации тем, что процесс роста является основой жизни, выражает ее внутреннюю сущность и тесно связан с другими важнейшими биологическими процессами и явлениями в организме.
Концептуальной основой функции роста Бакмана является постулат о том, что логарифм скорости роста отрицательно пропорционален квадрату логарифма времени
log H = k2 log2T. (2.1)
Константа
k2 всегда отрицательна. Однако это не значит, что скорость роста всегда снижается, в интервале 0 < T < 1 скорость будет увеличиваться, поскольку логарифм здесь отрицательный. Г.Бакман вводит показатель “нормальное время” (т.е. момент времени, в который скорость роста максимальна), принимаемый за единицу времени, и “нормальная скорость” (скорость роста в момент ее максимального выражения), принимаемую за единицу скорости. Поскольку при максимальном росте реализуется видоспецифическая генетическая программа данной особи, единицу времени, определенную таким образом, можно сравнить у организмов разных видов. Для определения кривой роста (y) по его скорости Г.Бакман выводит интегральную функцию 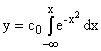 , (2.2)
, (2.2)
где
c0 — константа пропорциональности количественных значений роста к стандартному интегралу, x — мера органического времени, определяемая по формуле ![]() (2.3)
(2.3)
Формула (2.3) — это функция органического времени. Константа
c1 является скаляром органического времени, c2 выражает логарифмическое значение физической меры, которой измеряется время достижения половины конечных размеров (t0,5), взятое пропорционально скалярной величине c1. Отношение c1 и c2 — это логарифмическая мера применимости шкалы физического времени. С переходом от одной шкалы физического времени к другой изменяется лишь значение c2, возрастая по мере уменьшения единицы физического времени.Г.Бакман отмечает принципиальное сходство своей функции (2.3) с формулой времени динамического события, выведенной астрофизиком Э.Милном (Milne, 1937). Формула Милна имеет вид
![]() , (2.4)
, (2.4)
где
t — значение в исходный (современный) момент, t0 — возраст вселенной.§3. «Кванты жизни» и темпоральная акселерация
Г.Бакман считает, что значения
x2 = 0/2; 1/2; 2/2; ...; n/2 имеют особо важную биологическую сущность. Разность этих значений ![]() (3.1)
(3.1)
он назвал квантом жизни и утверждал, что
x2 организма в данный момент отражает число уже пережитых и еще предстоящих пережить квантов жизни.С увеличением возраста организма каждой следующей единице физического времени соответствует все меньше органического времени – происходит акселерация физического (кинематического) времени. Абсолютную акселерацию физического времени
Dt Г.Бакман определяет как количество t, соответствующее в различном возрасте постоянному интервалу органического времени Dx. Поскольку Dt зависит от c1, то эта величина различна не только для разных организмов, но и органов одного организма. Для устранения этой трудности Г.Бакман вводит понятие относительной акселерации физического времени как отношение показателя абсолютной акселерации любого года жизни tn к абсолютной акселерации данного года жизни tp. Относительная акселерация физического времени не зависит от типа роста, одинакова для различных органов и частей органов одного организма. Это как бы мера абсолютного возраста организма, отсчитываемого по “биологическим часам”. В отношении же психологического восприятия акселерации физического времени Г.Бакман представляет прошедшую часть жизни как единство, где, например, восьмой год от этого единства будет 1/8, а двадцатый соответственно 1/20. В общем виде 1 год — это 1/tn и год tp — это 1/tp от этого единства прожитой жизни.Для иллюстрации сравнения органического времени различных организмов с их возрастом приводится табл.1, заимствованная из книги Г.Бакмана (Backman, 1943). Как видно по данным табл.1, в начальный период своей жизни любой организм живет по отрицательному времени, которое в дальнейшем постепенно достигает нулевого состояния и переходит затем в положительное время. Например, человек через этот порог
(из отрицательного в положительное время) переходит примерно в 16 лет, сельдь — в 38,5 месяцев, мышь — в 12,8 недели и дафния — в 14 дней.Таблица 1
Сравнение ступеней возраста различных организмов
|
Органическое |
Физический возраст, считая с начала роста |
Физический возраст, считая с начала роста |
Физический возраст, считая с начала роста |
Физический возраст, считая с начала роста |
Физический возраст, считая с начала роста |
Физический возраст, считая с начала роста |
Физический возраст, считая с начала роста |
Физический возраст, считая с начала роста |
|||||||
|
время (x) III цикла |
Ячмень, дни |
Кукуруза, недели |
Дуб, годы |
Бук, годы |
Дафния, дни |
Сельдь, месяцы |
Человек, годы |
Мышь, недели |
|||||||
|
-2,63127 |
21 |
5,6 |
1,2 |
1,9 |
0,3 |
0,8 |
4,2 |
3,6 |
|||||||
|
-1,90920 |
27 |
7,1 |
3,7 |
5,1 |
0,9 |
2,0 |
4,8 |
3,7 |
|||||||
|
-1,52085 |
32 |
8,0 |
6,9 |
8,6 |
1,5 |
4,2 |
5,4 |
3,9 |
|||||||
|
-1,25359 |
35 |
8,8 |
10,5 |
12,4 |
2,2 |
6,2 |
6,1 |
4,1 |
|||||||
|
-1,04963 |
38 |
9,4 |
14,5 |
16,4 |
3,0 |
8,3 |
6,8 |
4,4 |
|||||||
|
-0,88464 |
41 |
9,9 |
18,8 |
20,5 |
3,8 |
10,6 |
7,6 |
4,8 |
|||||||
|
-0,74609 |
43 |
10,3 |
23,3 |
24,7 |
4,7 |
12,9 |
8,3 |
5,3 |
|||||||
|
|
44 |
10,5 |
24,8 |
26,0 |
5,0 |
13,7 |
8,6 |
5,4 |
|||||||
|
-0,34363 |
51 |
11,7 |
43,8 |
42,7 |
8,5 |
23,3 |
11,5 |
7,8 |
|||||||
|
-0,01309 |
58 |
13,1 |
73,5 |
66,9 |
13,7 |
37,8 |
15,8 |
12,5 |
|||||||
|
|
58 |
13,1 |
75,0 |
68,2 |
14,0 |
38,5 |
16,2 |
12,8 |
|||||||
|
0,22564 |
63 |
14,1 |
106,8 |
92,6 |
19,5 |
53,5 |
20,5 |
18,9 |
|||||||
|
0,41261 |
68 |
14,9 |
143,1 |
119,5 |
25,6 |
70,3 |
24,9 |
26,9 |
|||||||
|
0,56630 |
73 |
15,7 |
182,0 |
147,3 |
32,1 |
88,0 |
29,7 |
36,6 |
|||||||
|
|
77 |
16,4 |
226,6 |
178,4 |
39,4 |
108,1 |
35,0 |
48,9 |
|||||||
|
0,81022 |
80 |
17,0 |
266,6 |
205,3 |
45,8 |
125,7 |
39,6 |
60,9 |
|||||||
|
|
86 |
18,0 |
358,8 |
265,8 |
60,5 |
165,8 |
49,8 |
91,6 |
|||||||
|
1,15619 |
92 |
19,0 |
458,1 |
328,7 |
76,0 |
208,3 |
60,4 |
128,8 |
|||||||
|
|
94 |
19,4 |
510,0 |
360,8 |
84,0 |
230,2 |
65,8 |
150,1 |
|||||||
|
Значения констант в формуле (2.3) |
|||||||||||||||
|
с 1+ |
5,84044 |
7,18196 |
1,47114 |
1,69212 |
1,57380 |
1,57640 |
1,73818 |
1,01845 |
|||||||
|
с 2- |
10,29921 |
8,02419 |
2,75848 |
3,10252 |
1,80370 |
2,49900 |
1,89076 |
0,98142 |
|||||||
1
Момент органического времени соответствует моменту достижения половой зрелости.
§4. Опыт применения функции Бакмана
Функция Бакмана неоднократно обсуждалась в литературе. Положительно оценил возможность ее применения в лесобиологических исследованиях И.Век (Weck, 1953) и другие авторы. Обстоятельному критическому анализу подверг функцию Бакмана Х.Томазиус (Thomasius, 1965
). На основе формул Г.Бакмана он построил номограмму, с помощью которой можно по исходной информации быстро определить необходимые константы c0, c1, c2 и “органическое время” x. Проанализировав большой фактический материал, Х.Томазиус пришел к выводу, что функцию Бакмана можно использовать для аппроксимации эмпирических данных прироста деревьев по объему (массе), но эта функция мало подходит для отражения роста в высоту и по диаметру деревьев (без надлежащих коэффициентов пропорциональности). Он отмечает, что Бакманом не дан однозначный способ определения продолжительности второго (примордиального) цикла роста деревьев с указанием четких биологических критериев его границ, константам функции не даны достаточная биологическая интерпретация и измерения, к тому же эта функция для каждого цикла жизни имеет разные константы, что сильно осложняет ее применение.Результаты наших исследований с древесными растениями подтверждают вывод Х.Томазиуса в отношении исходной информации. Лучшие результаты дало использование количественных значений прироста по объему. Включение показателя собственного времени
x в математическую модель прогноза прироста древесины существенно повысило информативность модели (Мауринь, 1982). Интересные результаты были получены в исследованиях по применению функции Бакмана для диагностики потенциальной антропотолерантности деревьев. На Рижском взморье нами были выбраны участки, относительно гомогенные по антропогенной нагрузке, и из произрастающих на них деревьев сосны выделены выборки явно неустойчивых (деградирующих, усыхающих) и антропотолерантных (хорошего состояния). Для дальнейших расчетов были использованы данные о текущем приросте древесины этих совокупностей деревьев за восьмидесятилетний ретроспективный период. Значения функции Бакмана для этих двух совокупностей существенно различались и до периода отрицательного антропогенного воздействия. Деревья, оказавшиеся впоследствии антропотолерантными (устойчивыми), отличались большей кривизной (т.е. более ускоренным темпом) собственного времени в начальные периоды онтогенеза. Эти результаты показывают, что функцию Бакмана можно использовать для прогнозирования антропотолерантности деревьев. Однако для разработки конкретной методики применения этого принципа в селекционной работе необходимы дальнейшие исследования.Мы применили функцию Бакмана также для унифицированной формализации возрастности древесных растений (Мауринь, 1982). Представление о возрастности растений вошло в биологию благодаря работам Н.П.Кренке (Кренке, 1940). Однако выделяемые им признаки возрастности являются видоспецифическими, что служило препятствием к широкому применению этого подхода. Поэтому так актуальна задача унифицированной формализации возрастности. Один из способов решения этой задачи предложил А.А.Уранов (Уранов, 1975)
. Весь онтогенез растений он делит на 10 возрастных состояний: проростки (всходы), ювенильные, имматурные, виргинильные (молодые вегетативные), молодые (ранне-) генеративные, средневозрастные (зрелые) генеративные, старые (поздне-) генеративные, субсенильные (старые вегетативные), сенилъные и отмирающие (“почти труп”) растения. Приравняв единице количество энергии, воспринятое растением в течение всего онтогенеза, а возрастность особи, выразив долей энергии, которая освоена к середине данного возрастного состояния, он вывел формулу возрастности растения ![]() , (4.1)
, (4.1)
где
m — возрастность особи, t — этап возрастного состояния в баллах (0ё 10). Интересно отметить, что гипотеза А.А.Уранова об удлинении среднего времени пребывания особи в каждом последующем возрастном состоянии от подростков до зрелых генеративных особей соответствует правилу Г.Бакмана об акселерации физического времени в ходе онтогенеза. Определенный интерес представляет сопоставление данных о возрастных состояниях и возрастности по А.А.Уранову с соответствующими этим этапам интервалами органического времени, вычисленными нами по формуле Бакмана для сосны обыкновенной (табл.2). Поскольку биологическое время (по функции Бакмана) в начале онтогенеза имеет отрицательное значение, интервалы его (“кванты жизни”) в последней графе таблицы для j, im, v, g1 также отрицательны. Количественные значения интервалов органического времени округлены доФормализация возрастности растений функцией Бакмана нами применялась для прогнозирования скороплодности древесных растений (Мауринь, 1987). Модельным объектом служили однолетние сеянцы абрикоса обыкновенного в Ботаническом саду Латвийского университета (Рига). Отмечалась дата появления каждого всхода, а затем измерялась его длина через
5—7 дней. У большинства сеянцев четко проявились две волны прироста за вегетационный период, у остальных сеянцев эти две волны в какой-то мере перекрывались, однако траектория общего прироста все же образовывала двухвершинную кривую. Поэтому разделение кривых первого и второго приростов и тут не составляло трудностей. Для первого и второго приростов функция Бакмана вычислялась отдельно, поскольку константы функции различались. Однако выявилась общая закономерность: более акселерированные (т.е. с ускоренным темпом органического времени) по обoим приростам сеянцы впоследствии выделялись своей скороплодностью. Они заплодоносили в четырехлетнем возрасте, тогда как основная масса сеянцев — лишь на шестом-седьмом году жизни. У потенциально скороплодных однолетних сеянцев визуально были заметны признаки относительно большей возрастности по Н.П.Кренке (Кренке, 1940): большее число листьев на единицу длины побега, более резкий переход в форме листьев (от проростковой к взрослой), появление боковых побегов.Таблица 2
Возрастные состояния и органическое время в онтогенезе сосны обыкновенной
|
Возрастные состояния |
Индекс / балл |
Возрастность особей (m i) |
Интервалы органического времени (III цикл) |
||
|
Проростки (всходы) |
p/1 |
0,0067 |
I—II и начало III цикла роста |
||
|
Ювенильные растения |
j/2 |
0,0180 |
|
||
|
Имматурные растения |
im/3 |
0,0474 |
|
||
|
Виргинильные (молодые вегетативные) растения |
v/4 |
0,1192 |
|
||
|
Молодые (ранне-) генеративные растения |
g1/5 |
0,2700 |
|
||
|
Средневозрастные (зрелые) генеративные растения |
g2/6 |
0,5000 |
|
||
|
Старые (поздне-) генеративные растения |
g3/7 |
0,7310 |
|
||
|
Субсенильные (старые генеративные) растения |
ss/8 |
0,8808 |
|
||
|
Сенильные растения |
s/9 |
0,9529 |
|
||
Следовательно, тренд автотемпоральности (возрастности), описываемый функцией Бакмана, уже в начальные этапы онтогенеза отражает биологическую диспозицию (предрасположение) особи. Этот аспект представляет не только прикладное значение для разработки методики прогнозирования дальнейшего развития организма в тех или иных условиях. Функция Бакмана может послужить конструктивным средством однопозиционной интерпретации вероятности, методологически обоснованной К.Р.Поппером (Поппер, 1983). однако прежде чем отвести такую роль этой функции, необходимо знать, в какой мере ее количественное значение детерминируется генотипом организма и в какой — изменениями окружающей среды. Сам Г.Бакман, исходя из формальных соображений и анализа результатов экспериментальных исследований, пришел к выводу, что “внешние усложнения не влияют на
c1 и, по-видимому, значение c1 здесь определяется генетическими факторами. В то же время очевидно, что численное значение c2 может быть легко модифицируемо путем изменения внешних условий” (Backman, 1943, с.169). Вывод Г.Бакмана мы пытались проверить на объектах своих исследований. Индивидуальные различия между деревьями одной ценопопуляции по константе c2 всегда оказывались существенно больше, чем по константе c1. Анализ хода роста сосны обыкновенной, участок насаждения которой двадцать семь лет назад был подвергнут мелиорации, показал, что после осушения характер органического времени деревьев резко меняется, в основном из-за изменения константы c2. Правда, несколько менялось и количественное значение константы c1. Но, может быть, в результате такой сильной “встряски” (резкое улучшение аэрации почвы после ее осушения) произошли какие-то изменения и в генотипе дерева, например, переход части оцепленных (взаимосвязанных) генов в аддитивное состояние?Соотношение количественных значений констант
c2 и c1, как это уже отмечалось выше, имеет фундаментальное значение в детерминации онтогенеза. Это же соотношение Г.Бакман использовал для выведения формулы потенциальной продолжительности жизни организма ![]() . (4.2)
. (4.2)
Числитель второго слагаемого формулы (4.2) — это теоретическая продолжительность жизни в органическом времени (т.е.
x »Функцию Бакмана мы использовали также для определения темпоральной (функциональной) гармонии как показателя адаптированности древесных растений (Мауринь, 1979). Концептуально такой подход основывается на представлении об адаптации как гармонии организма (популяции, вида) со средой обитания (Яблоков, Юсуфов, 1981). Как пишет Э.М.Сороко (Сороко, 1984), гармония — это устойчивое единство разнообразия, осуществляющееся вблизи определенных узловых точек (инвариантов) состояния (распределенности частей) системы:
![]() , (4.3)
, (4.3)
где ![]() — относительная энтропия системы (мера распределенности частей целого),
— относительная энтропия системы (мера распределенности частей целого),
В сложных системах с внутренне структурированной относительной энтропией, заданной частотным распределением компонентов
p1, p2, ..., pn, имеем ![]() , (4.4)
, (4.4)
где
n — число состояний (событий, частей в целом и т.п.).Для аппроксимации темпоральной (функциональной) гармонии в качестве
pi мы брали интервалы физического (календарного) времени, соответствующие “квантам жизни” как структурной единице органического времени. Темпоральная гармония вычислялась для деревьев автохтонных (местных) видов и интродуцентов, индивидуально различающихся по своему состоянию. В табл.3 приводятся данные по местным видам ели и сосны, а также по интродуцентам — пихте одноцветной, лиственнице Сукачева, ели ситхинской, сосне Банкса и веймутовой, лжетсуге Мензиса и туе гигантской, культивируемым в Латвии и Калининградской области. Причина деградации деревьев местных видов сосны и ели — длительное воздействие неблагоприятных антропогенных факторов. Из данных, приведенных в табл.3, видно, что чем ближе количественное значение S к целочисленному, тем дерево в лучшем состоянии и наоборот. Весьма интересен вопрос биологической интерпретации смены S-алгоритмов (S = 1, 2, 3 и т.д.), соответствующих определенным устойчивым состояниям в процессе адаптации растений. Для корректного ответа на этот вопрос требуются дальнейшие исследования.Таблица 3
Общее состояние и уровень функциональной гармоничности деревьев
|
Наименование вида |
Возраст, годы |
Высота, м |
Диаметр ствола, см |
Состояние дерева |
|
S |
|
Автохтонные виды |
|
|
|
|
|
|
|
Picea abies (L.) Karst. |
74 |
23 |
39 |
отличное |
0,6847 |
2,02 |
|
P. abies (L.) Karst. |
78 |
20 |
34 |
деградированное |
0,7011 |
2,40 |
|
Pinus sylvestris L. |
96 |
27 |
37 |
отличное |
0,6162 |
0,98 |
|
P. sylvestris L. |
92 |
21 |
31 |
деградированное |
0,6531 |
1,49 |
|
Интродуценты |
|
|
|
|
|
|
|
Abies concolor (Gord.et Glend) Lindl.ex Hildebr. |
78 |
24 |
38 |
хорошее |
0,6849 |
2,05 |
|
Larix russica (Endl.) Sabine ex Trautv. |
74 |
32 |
48 |
хорошее |
0,6872 |
2,10 |
|
Picea sitchensis (Bong.) Carr. |
76 |
18 |
34 |
удовлетворительное |
0,6930 |
2,22 |
|
Pinus banksiana Lamb. |
64 |
14 |
36 |
удовлетворительное |
0,7340 |
3,28 |
|
P. strobus L. |
74 |
20 |
51 |
вполне удовлетворительное |
0,6703 |
1,85 |
|
Pseudotsuga menziesii (Mirb.) Franco |
78 |
22 |
47 |
очень |
0,7253 |
3,02 |
|
P.menziesii (Mirb.) Franco |
76 |
15 |
34 |
вполне удовлетворительное |
0,7308 |
3,19 |
|
Thuja plicata Donn |
92 |
28 |
52 |
хорошее |
0,6090 |
0,89 |
Концепция органического времени Г.Бакмана по своей теоретической обоснованности, методологической и методической проработке занимает фундаментальное место в биотемпорологии. Следует отметить, что временны
ў е отношения в живой природе он понимал в неразрывной связи с пространственными аспектами. “Итак, — писал он, — я считаю, что живые организмы развиваются в логарифмическом мире, где пространственные и временныў е измерения имеют логарифмический масштаб” (Backman, 1943, с.4З). Впрочем, проблема пространственно-временныў х состояний и отношений в живой природе — это предмет отдельного размышления.К темпорологическим выводам Г.Бакмана приходит известный математик-системолог Б.С.Флейшман (Флейшман, 1986), разрабатывая проблему адаптации регенерирующих систем в контексте развиваемой им теории потенциальной эффективности сложных систем. Он пишет, что полученные им результаты хорошо соответствуют “закону Бакмана”. Причем здесь “вопрос не в лучшей математической аппроксимации эмпирических данных”, а в том, что “логарифмические кривые роста являются следствием оптимизационных законов системологии, и устойчивость биосистем здесь понимается как их высокая надежность, обеспечиваемая минимальным порядком роста их элементов” (Флейшман, 1986, с.95).
ЛИТЕРАТУРА
КРЕНКЕ Н.П. Теория циклического старения и омоложения растений и практическое ее применение. М., 1940.
МАУРИНЬ А.М. Проблема биологического времени и функция Г.Бакмана // Моделирование и прогнозирование в экологии. Рига, 1982. С.73
МАУРИНЬ А.М. Проблема прогноза и увеличения долговечности деревьев в городской среде // Проблемы комплексного управления городской средой. Материалы всесоюзной научной конференции. Львов, 1979. С.99
- 100.МАУРИНЬ А.М. Проблема разработки онтогенетической шкалы биологического времени // Моделирование и прогнозирование в биоэкологии. Рига, 1982. С.73
- 81.МАУРИНЬ А.М. Возрастность как интегральный показатель для прогноза скороплодности интродуцентов // Вопросы обогащения генофонда в семеноведении интродуцентов. Тезисы докладов. М., 1987а. С.78
- 79.МАУРИНЬ А.М. Функциональная гармония как показатель для мониторинга лесных экосистем // Биомониторинг лесных экосистем. Материалы школы-семинара. Каунас, 1987б. С.30
- 31.ПОППЕР К.Р. Логика и рост научного знания. Избранные работы. М., 1983.
СОРОКО Э.М. Структурная гармония систем. Минск, 1984.
УРАНОВ А.А. Возрастной спектр фитоценопопуляции как функция времени и знергетических волновых процессов // Научные доклады высшей школы. Биологические науки. 1975. №2. С.7
- 34.ФЛЕЙШМАН Б.С. Темпорально-биологический “закон логарифма” как следствие общесистемного гиперболического закона надежности регенерирующих систем // Темпоральные аспекты моделирования и прогнозирования в экологии. Рига, 1986. С.85
- 97.ЯБЛОКОВ А.Б., Юсуфов А.Г. Эволюционное учение. М., 1981.
BACKMAN G. Uber generalle Wachstumgesetze beim Menschen // Acta Univers. Latviensis. 1925. Bd.12. S.367
- 380.BACKMAN G. Wachstum und Organische Zeit. Leipzig. 1943.
DOUGLASS A.E. Crossdating in dendrochronology // Journal of Forestry. 1941. №39(10). P.825
- 831.MILNE E.A. Kinematics, Dynamics and the Scale of Time. Proc. Roy.Soc.Lond. Ser.A. 1937. V.158. P.321.
THOMASIUS H. Kritik der Wachstumfunktion von G.Backman // Wissenschaftliche Zeitschrift der Technischen Universitat Dresden. 1965. №14. в.4. S.1019
- 1031.WECK J. (1953). Anwendung von Wuchsgesetzen als Metode der fortlichen Zuwachsforschung // Allgemeine
Forstzeitschrift. №4. P.29 - 43.