К вопросу об
отображении реальности сознанием
наблюдателя
А. М. Заславский
г.
Днепропетровск, Украина
В работе
изложены принципы построения и результаты исследования математической модели
одного из возможных механизмов пространственного отображения реальности
сознанием наблюдателя. Реальность
изначально предполагается заданной не в пространстве, а лишь
последовательностью событий во времени. Исследованы некоторые геометрические и
кинематические закономерности пространства-времени, в котором отображается
последовательность событий наблюдаемой реальности. Разработана математическая
модель механизма репликации пространственного базиса в популяции наблюдателей.
Введение
Хью Эверетт в своей известной
работе [1], которая в последнее время
всё чаще цитируется в связи с так называемой «проблемой измерений» в квантовой
механике, предложил следующую модель наблюдателя. «В качестве модели для наблюдателей мы, если пожелаем, можем
рассматривать автоматически функционирующие машины, обладающие чувствительным
датчиком, связанным с регистрирующим устройством и способные к регистрации
прошлых сенсорных данных и конфигураций машины. … Эти конфигурации могут
рассматриваться как отверстия в бумажной ленте, след в магнитной катушке,
конфигурации переключающих реле, и даже как конфигурации ячеек мозга. Мы только
требуем, чтобы они были способны к интерпретации: "наблюдатель испытал
последовательность событий
C B A ,..."»[1].
Проблема включения модели сознания наблюдателя в ту конструкцию, которую мы
называем реальностью, выходит за рамки исключительно физических концепций и
методов. Эта мысль, например, в работах М.Б. Менского [2,3] уже приобретает черты своеобразной научной программы. Тем не
менее, во всех известных физических моделях наблюдатель присутствует в пространстве с
a priori заданной геометрией лишь в качестве
физического объекта (тела) наряду с другими, наблюдаемыми им физическими
объектами. Альтернативные модели, в которых пространство с его геометрией создаётся сознанием наблюдателя,
воспринимающего только формальную последовательность событий во времени, физика
не рассматривает. Развиваемая в данной работе идея построения математической
модели абстрактного наблюдателя,
способного осознать физические законы наблюдаемой им реальности, отталкивается
от кибернетических и теоретико-системных представлений. Альтернативность
предлагаемой модели проявляется уже в том, что последовательность событий C B A ,..., о которых шла речь в приведенной выше цитате,
рассматривается как абстрактное линейно упорядоченное множество, не отражающее
какую либо заранее заданную конфигурацию состояний физической реальности в
пространстве. Напротив, предполагается, что сама по себе линейная
упорядоченность и структурированность этого множества является достаточным
основанием для возникновения в сознании наблюдателя геометрических образов,
движущихся в пространстве.
Возможно, в
дальнейшем подобный подход окажется полезным не только для выяснения механизмов
отображения реальности сознанием, но и для ответа на вопросы об общих причинах физических
законов.
1.
Содержательная постановка задачи
Представим
себе некое устройство – кибернетический
ящик, на вход которого подаётся лента с нанесенными на ней тем или иным способом символами. Пусть в составе ящика в качестве
одной из его подсистем имеется автоматическое устройство или программа – виртуальный наблюдатель, который различает
символы как события в той реальности, с которой он соприкасается посредством
ленты. Символы на ленте могут быть представлены чем угодно: буквами, нотами,
цветами и т.п. Важно то, что наблюдатель различает символы, которыми кодируются
состояния наблюдаемой им реальности, и регистрирует в памяти распределение
частот их появления в цепи событий. Каждому классу состояний в цепи событий
ставится в соответствие координата в пространстве. Пусть, например, цепь
событий представлена последовательностью трёх
классов состояний a,a,b,c,b,b,a,c,c,c,… . Этой
последовательности в предлагаемой модели соответствует участок траектории точки
в трёхмерном пространстве. Приращения
координат точки на отрезке времени определяются
по количеству повторений состояний каждого класса A,B,C относительно состояний
некоторого объекта (подсистемы), выбранного в качестве «тела» отсчёта. При таком подходе каждое отдельно взятое
событие (момент времени) в рассматриваемом виртуальном мире не может быть
содержательно интерпретировано сознанием наблюдателя. Только последовательности
событий может быть поставлен в соответствие
некий объект (в простейшем случае – точка) в пространстве.
Зададим себе вопросы, какие
геометрические, кинематические и динамические законы движения в пространстве
может открыть для себя подобный наблюдатель, анализируя не предопределенную заранее
произвольную
последовательность символов на ленте. Можно ли предположить, что эти
законы формулируются так же как известные нам из нашего опыта? Можно ли
допустить, что пространство является не объективной данностью текущего момента
времени, а специфическим образом реальности в сознании наблюдателя, учитывающим
её историю. Может ли этот образ
конгруэнтно сформироваться в памяти популяции простейших автоматов или
живых существ вследствие естественного
отбора?
Все
известные физические теории изначально исходят из предположения о существовании
пространства с определённой геометрией, в котором протекают процессы,
подчиняющиеся эмпирическим законам
наблюдаемого мира. Модели, в которых пространство, заполненное движущимися
объектами, возникает в сознании
наблюдателя как отображение статистики
распределения состояний в цепи событий,
не исследовались.
2. Математическая модель наблюдателя абстрактной системы
Рассмотрим
некий виртуальный мир в виде взаимосвязанной системы абстрактных автоматов,
включающей наблюдателя и 
наблюдаемых им подсистем. Пусть, например, автомат – наблюдатель, как было предложено выше,
получает информацию из внешней среды посредством сигналов, передаваемых
бесконечной лентой, движущейся в одном направлении. Событие в системе будем
обозначать переменной 
, принимающей в каждый момент времени 
одно из 
различных значений 
, соответствующих 
возможным состояниям 
-той подсистемы. Число будем называть размерностью подсистемы. Событие состоит в том, что в
момент времени одна (и только одна) из подсистем (-тая), находясь в 
- том состоянии, воздействует на вход наблюдателя 
. Состояние входа
переходной функцией, учитывающей предысторию, отображается во внутреннее
состояние автомата - наблюдателя 
, где 
– предыстория (состояние
памяти наблюдателя). Иными словами, в
рассматриваемой модели предполагается,
что наблюдатель имеет возможность различать подсистемы и их состояния, а также,
что изменение внутреннего состояния наблюдателя всегда имеет своей причиной воздействие
на его вход в каждый момент времени только одной из взаимодействующих с ним
подсистем.
Идея
пространства в системе, где все события не одновременны и строго упорядочены,
может возникнуть лишь вследствие ограниченной возможности наблюдателя различать
их порядок следования на малых промежутках времени. В пределах такого
промежутка состояния как бы присутствуют одновременно. Поэтому для их
отображения требуется многомерный геометрический объект – вектор, отнесенный к
рассматриваемому малому промежутку как к моменту времени.
Пусть на отрезке времени между событиями 
и 
-тая подсистема характеризуется распределением количеств
повторяющихся состояний
. (2.1)
Это означает, что среди множества
событий, произошедших на рассматриваемом участке цепи событий, наблюдаемая
подсистема оказалась в первом состоянии 
раз, во втором состоянии
раз и т.д. Однако,
субъекту той виртуальной реальности, которую мы рассматриваем, сами по себе эти
числа ничего не говорят. Для того чтобы ориентироваться в своём мире, ему
необходимы относительные измерения,
подобные тем, которые в механике осуществляются в отношении тела отсчёта, с которым связывается
система координат и часы. В мире автоматов, где пространство a priori не задано, было бы не корректно использовать понятие
тела. Поэтому будем называть объектом
начала отсчёта 
- тую подсистему, относительно которой отображаются изменения состояний наблюдаемой - той подсистемы. Пусть объект начала отсчёта на
рассматриваемом отрезке времени характеризуется распределением
.
(2.2)
На рисунке 1 показан пример участка цепи
событий системы, включающей две подсистемы, каждая из которых может пребывать в
одном из двух состояний
Рис. 1. Пример участка цепи событий. Прямоугольниками
показаны состояния первой подсистемы, окружностями – второй. Затушёванные
фигуры соответствуют первым состояниям, не затушеванные – вторым.
В этом примере 
, 
, 
, 
.
Сделаем некоторые предположения о
конструкции той части сознания простейшего наблюдателя, которая отвечает за
создание пространственного образа реальности. Будем считать, что наблюдатель
обладает памятью, состоящей из регистров. Каждый 
- тый регистр
образован ячейками, пронумерованными от 
до 
, где 
- некоторое (в пределе бесконечное) число
натурального ряда. Ячейки регистров могут пребывать в одном из двух состояний –
активированном или не активированном. Можно предположить такую конструкцию
памяти простейшего наблюдателя, при которой в каждом регистре допустима только
одна активированная ячейка. В таком случае изменение состояния наблюдателя на
рассматриваемом отрезке времени при отображении - той подсистемы
относительно - той характеризуется
распределением
,
(2.3)
где 
представляет собой
изменение номера активированной ячейки
- того регистра памяти
наблюдателя при регистрации событий на его входе.
Вторым атрибутом сознания является
оператор 
отображения реальности
в памяти наблюдателя
.
(2.4)
Для того чтобы раскрыть содержание этого
оператора, необходимо сформулировать основные принципы (аксиомы) отображения
реальности абстрактным наблюдателем.
Прежде всего, рассмотрим вопрос о
нумерации регистров в его памяти. Во всех доступных наблюдению системах
физических тел порядок нумерации координат пространства может быть до некоторой
степени произвольным. Но, выбрав тело отсчёта, наблюдатель связывает с ним
систему координат, пронумерованную в определённом порядке. Все остальные тела
рассматриваются относительно этой системы координат.
Принцип нумерации состояний. Подобно тому, как в механике порядок
нумерации координат пространства устанавливается для тела отсчёта, в нашей
модели порядок нумерации регистров в памяти наблюдателя должен определяться
порядком нумерации состояний объекта начала отсчёта. Это означает, что индексом обозначается такое
состояния подсистемы, выбранной в
качестве объекта начала отсчёта, которое регистрируется в - том регистре памяти наблюдателя.
.
(2.5)
При таком подходе наблюдатель
«настраивается» на подсистему, выбранную в качестве объекта начала отсчёта и
получает возможность сравнивать с ней поведение других подсистем.
Принцип линейного отображения
реальности. Цепь событий может быть разбита на участки
таким образом, что в пределах каждого участка изменение 
вектора состояния внутреннего наблюдателя является линейной функцией количеств
повторяющихся состояний наблюдаемых подсистем и объекта начала отсчёта
,
(2.6)
где коэффициенты 
, не изменяются при изменении объекта начала отсчёта, а коэффициенты 
не изменяются при изменении объекта наблюдения, но первые
могут изменяться при изменении объекта наблюдения, а вторые – при изменении
объекта начала отсчёта. Иными словами – воздействие, оказываемое на наблюдателя
объектом наблюдения, не зависит от выбора объекта начала отсчёта и наоборот.
Такой участок цепи событий, на котором выполняется принцип линейного
отображения реальности, будем считать малым.
Может создаться впечатление, что наблюдатель, определяемый выражением (2.6) представляет собой сложное вычислительное устройство. Однако на самом деле алгоритм наблюдателя может быть реализован простейшим автоматом, с линейной тактикой поведения.
Пусть,
например, наблюдатель отображает цепь событий в одномерном пространстве
,
(2.7)
где - некоторый
фиксированный индекс.
Рассмотрим
автомат, который устроен следующим образом. Его вход регистрирует только
состояния вида подсистем и . При этом, если события 
повторяются в системе более чем 
раз, то номер
активированной ячейки его памяти
увеличивается на единицу. Если же
события 
повторяются в системе более чем 
раз, то номер
активированной ячейки памяти автомата уменьшается на единицу. После очередного
изменения номера активированной ячейки памяти счёт повторений событий
начинается с нуля. Граф переходов
такого автомата показан на рисунке 2.
Рис.
2. Граф переходов автомата – наблюдателя с линейной тактикой поведения
На отрезке
времени изменение номера активированной ячейки в памяти автомата будет равно
,
(2.8)
где 
обозначена дробная
часть отношения двух чисел, а фигурные скобки обозначают выделение целого.
При
достаточно больших величинах 
и 
дробными частями
отношений в выражении (2.8) можно пренебречь и тогда оно преобразуется к виду
(2.7), где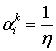 
, 
.
Так как в
памяти наблюдателя регистрируются изменения состояний в количествах 
и 
(а не 
и 
), то эти изменения будем называть ощутимыми для наблюдателя.
Подобные
конструкции автоматов были исследованы М.Л. Цетлиным [4], который показал, что
с увеличением объема памяти их поведение асимптотически приближается к
оптимальному, если под оптимальным поведением понимать адекватную реакцию на
состояния наблюдаемых подсистем. Пусть, например, положительные значения номера активированной
ячейки соответствуют адекватной реакции автомата на появление - того состояния - той подсистемы, а
отрицательные значения – неадекватному.
И наоборот, отрицательные
значения номера активированной ячейки соответствуют адекватной реакции автомата
на появление - того состояния
- той подсистемы, а
положительные значения – неадекватному. При случайном чередовании событий и реакция автомата может
быть адекватной и неадекватной. Но с увеличением объема памяти (в нашем случае,
измеряемого числом ) согласно результатам, полученным М.Л.Цетлиным, вероятность
адекватной реакции автомата с линейной тактикой асимптотически стремится к
максимально возможной.
Обращает нас себя внимание следующее:
рассмотренный автомат имеет чрезвычайно простую конструкцию,
напоминающую конструкцию нейрона,
который изменяет своё состояние, когда взвешенная сумма входных сигналов
(событий) превышает некоторое пороговое значение. Он способен адаптироваться к
условиям случайной среды, объединяя ресурс памяти с другими автоматами. Система
таких автоматов способна выполнять ту функцию нашего сознания, которая
отображает наблюдаемую нами цепь событий в многомерном пространстве (см.
рис.3). Из этого следует, что понятие пространства и способность отображения
реальности в пространстве могут быть продуктами естественного отбора в
популяции простейших автоматов или живых существ.
Рис.3. Отображение состояния наблюдаемых подсистем в пространстве
(активированные ячейки памяти отмечены чёрным цветом, соответствующие
точки, указывающие относительное положение подсистем в пространстве – серым
цветом).
Целью
анализа модели наблюдателя является нахождение таких математических
зависимостей, из которых можно было бы в явном виде получить коэффициенты и . Зная их,
можно решать задачи, являющиеся, в
некотором смысле, обратными по отношению к задачам квантовой механики.
Там по известной реакции на взаимодействие в пространстве и времени
макроскопической системы с квантовым объектом вычисляется распределение
вероятностей (частот) состояний квантового объекта.
Здесь же по
известному распределению количеств повторений (частот) состояний наблюдаемой
подсистемы в цепи событий вычисляется
пространственный (траекторный) образ её движения в сознании наблюдателя.
3. Метрические отношения в пространстве – времени абстрактной системы
Для того чтобы выявить общие
закономерности отображения цепи событий абстрактной системы в пространстве –
времени внутреннего наблюдателя необходимо определить элементарные мерные
отрезки, которыми должны измеряться длительность и протяжённость. Пусть такими
отрезками будут: квант времени 
и
квант расстояния 
, где -
величина, соответствующая длительности промежутка времени между двумя,
следующими непосредственно друг за другом событиями, а 
-
масштабный коэффициент. Обе величины и являются произвольными константами,
определяющими выбор единиц измерения пространства и времени.
В задачах, связанных с относительным
движением тел в доступном нашему наблюдению физическом пространстве, используют
для измерения собственного времени наблюдателя часы, покоящиеся относительно
тела отсчёта. В нашей модели математическим эквивалентом такого тела является
подсистема – объект начала отсчета. Покой относительно объекта начала отсчёта для подсистемы, рассматриваемой
в качестве часов, означает одинаковое с ним распределение повторяющихся
состояний на общем отрезке цепи событий. Показания часов – это количество
изменений состояний объекта начала отсчёта. Так как все события в рассматриваемой системе линейно
упорядочены, то для любого отрезка цепи событий 
- той
подсистемы количество событий, связанных с наблюдением объекта начала
отсчёта,
равно суммарному количеству всех его состояний
.
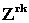Здесь и далее рассматривается макроскопический пространственный образ
реальности, порождаемый цепью событий большой плотности (
).
Промежуток времени, измеряемый внутренним наблюдателем, равен произведению количества
наблюдаемых событий на величину кванта времени
(3.1)
Величина
(3.2)
представляет собой протяжённость (интервал) цепи ощутимых
событий подсистемы – объекта начала отсчёта . Этот интервал представлен суммой
мерных отрезков величиной , взятых в количестве 
.
В течение
времени 
внутренний наблюдатель ощутит изменений собственного вектора
состояния 
, вызванных изменениями - того состояния объекта начала отсчёта.
Следовательно, единичному изменению - того состояния он может поставить в
соответствие мерный отрезок протяжённостью 
. Этот отрезок остаётся неизменным
эталоном протяжённости пространства при измерении параметров движения любых
подсистем относительно -
той подсистемы. Измеряя этими отрезками относительное движение - той подсистемы в направлении - той координатной оси – 
в
собственном метрическом пространстве, внутренний наблюдатель получит 
. Умножив обе части (2.6) на
величину и
произведя соответствующую замену переменных, найдём
, (3.3)
где: 
(3.4)
Итак,
распределение состояний в цепи событий 
характеризует некоторую подсистему с внешней
стороны. На этом же участке цепи событий внутренний наблюдатель отобразит в
своём сознании вектор 
, который описывает перемещение точки,
отображающей наблюдаемую им подсистему, в пространстве. Связь между двумя описаниями реальности
задаётся коэффициентами и
. Зная эти коэффициенты, можно по известному
распределению состояний в цепи событий построить траекторию движения
наблюдаемой подсистемы в пространстве. Образно говоря, «переместиться» из того
мира, где эволюция наблюдаемой системы представляется последовательностью
абстрактных событий, определённых только во времени, в мир, где эта же эволюция
представляется траекториями движения тел в пространстве.
4. Линейные преобразования в пространстве – времени
абстрактной системы
Из (3.3) следует, что, наблюдая k-тую подсистему относительно 
- той и - той подсистем, внутренний наблюдатель
обнаружит следующие соотношения
,
(4.1) 
. (4.2)
Отсюда, согласно принципу линейного отображения реальности, вытекает
очевидное равенство
, (4.3)
где 
.
(4.4)
В общем случае, учитывая возможность перемещения подсистем в пространстве
во взаимно противоположных направлениях относительно координатной оси,
результаты наблюдений внутреннего наблюдателя могут быть представлены в виде
, (4.5)
. (4.6)
Выразив коэффициенты 
и 
через новые коэффициенты 
и 
,
(4.7)
,
(4.8)
получаем
,
(4.9)
.
(4.10)
Пусть - тая подсистема будет неподвижна
относительно -той подсистемы, тогда 
, а
.
Следовательно, рассматривая движение - той подсистемы относительно - той имеем
.
(4.11)
Обозначив 
модуль скорости, с которой подсистема движется относительно в
направлении оси 
при условии, что 
, 
, находим
.
(4.12)
Перемножив, соответственно, правые и левые части (4.5) и (4.6), получим
. (4.13)
Для
того чтобы найти величину 
отождествим - тую подсистему с - той. В таком случае 
, 
, а из (4.13) следует
. (4.14)
Теперь
отождествим -тую подсистему с -той. В таком случае 
, 
, а из (4.13) следует
. (4.15)
В том и
другом случае величины и не изменяются, так как определяются согласно
(4.4) выбором подсистем и
, которые остаются прежними.
Из
(4.14) и (4.15) следует
. (4.16)
Для
того чтобы это равенство и равенство (4.13) могли выполняться совместно произведение
должно удовлетворять уравнению второго порядка
.
(4.17)
Это уравнение имеет два решения 
и 
.
Из первого следует предельный случай движения 
, 
. Второе
решение соответствует группе допустимых движений, при которых 
. Этими двумя решениями
исчерпываются все виды допустимых движений в пространстве внутреннего
наблюдателя. Так как из (4.17) следует, что величины и
имеют одинаковые знаки, то согласно (4.12), масштабная константа определяет наибольшую возможную
скорость этих движений. Подставляя решение в
(4.16), получим
.
Это равенство свидетельствует об
инвариантности величины 
(4.18)
к выбору объекта начала отсчёта. Если в
качестве объекта начала отсчёта выбрать саму -тую подсистему, то 
и выражение (4.18) приводится
к виду (3.2), где 
. Следовательно величину 
можно отождествить с интервалом мировой линии -
той подсистемы в пространстве событий внутреннего наблюдателя. Такой вид интервал имеет в частном случае,
когда направление относительного движения наблюдаемой подсистемы совпадает с
направлением одной из пространственных осей. В общем случае, при произвольном
направлении координатных осей относительно
неизменного направления
движения подсистемы, выражение для интервала может быть приведено к виду
. (4.21)
При условии из (4.7, 4.8, 4.12) найдём значения
коэффициентов и
, 
.
Подставляя
полученные коэффициенты в (4.9) и (4.10), получаем известные формулы
преобразования Лоренца
,
.
При
выводе этих формул использовалась хорошо известная в СТО схема рассуждений [5]. Тем не менее, имеются некоторые существенные
отличия приведенных рассуждений от классических.
Во-первых, источником информации для нашего анализа являются не
геометрические объекты («твёрдые» стержни и шкалы часов), определяющие место и
время событий в изначально заданном четырёхмерном многообразии, а
параметры (количества повторений состояний), которые непосредственно
характеризуют распределение событий только во времени. Как видно из вышеизложенного,
эти параметры для внутреннего наблюдателя абстрактной системы определяют
протяжённость траекторий и длительность процессов подобно отрезкам прямых линий и интервалам времени.
Во-вторых, при выводе
преобразований Лоренца в СТО равенство
единице произведения , устанавливающее инвариантность
интервала, является результатом соглашения о постулируемых свойствах (однородность и изотропность) пространства –
времени [6]. Здесь же мы
воспользовались тем обстоятельством, что в рассматриваемой модели это произведение
зависит лишь от выбора объектов начала
отсчёта и , но не зависит от выбора объекта
наблюдения (-той подсистемы). Следовательно,
изотропность и однородность отображаемого наблюдателем пространства-времени
обусловлены тем, что воздействие, оказываемое на наблюдателя наблюдаемым
объектом, не зависит от выбора объекта начала отсчёта (см. принцип линейного
отображения реальности).
В-третьих, ограничение предельной скорости движения объектов в
пространстве и её инвариантность к преобразованиям системы отсчёта в отличие от
ключевой идеи СТО, здесь является не постулатом, а следствием линейной
упорядоченности состояний в цепи событий. Скорость точки в пространстве
внутреннего наблюдателя ограничена постольку, поскольку количество состояний любой подсистемы, определённой на линейно
упорядоченном множестве, не может превысить количества событий во включающей её
системе.
Допустим, внутренний наблюдатель абстрактной системы обладает достаточным
интеллектом для анализа относительных движений наблюдаемых подсистем в
собственном виртуальном пространстве в достаточно малой окрестности некоторой
его точки. Вследствие вышеизложенного он неотвратимо придёт к выводу о том, что
они соотносятся между собой так, как того требуют преобразования Лоренца. А это означает, что для автомата – наблюдателя
СТО является математическим следствием линейной упорядоченности цепи событий и
может быть «открыта» им в результате измерения скоростей относительных движений
виртуальных объектов подобно тому, как это произошло в нашей истории в
результате измерения скоростей распространения электромагнитных волн и
относительных движений реальных объектов.
5. Внедрение наблюдателя в абстрактную систему
Для
того чтобы построить модель внутреннего наблюдателя абстрактной системы, т.е.
найти коэффициенты и
, которыми он определяется согласно
уравнениям (2.6, 3.3, 3.4), нам потребуется выразить приращение интервала и
скорость относительного движения подсистем 
через величины , непосредственно описывающие
распределение состояний в цепи событий.
Пусть
система координат в пространстве внутреннего наблюдателя выбрана таким образом,
что движение - той подсистемы осуществляется либо в
направлении координатной оси , либо в противоположном направлении, а
в направлении иных координатных осей движение отсутствует , .
В
первом случае согласно (3.3) имеем
.
Второй
случай отличается от первого лишь направлением движения относительно направления
координатной оси. Это означает, что уравнение (3.3) может быть записано для
другого объекта начала отсчёта в виде
,
где: 
, а 
Выполнив соответствующие
подстановки и перемножив, правые и левые части уравнений для первого и второго
случаев движения, получим
.
Выше была
доказана инвариантность интервала к выбору объекта начала отсчёта. Это
означает, что произведение 
может зависеть только
от величин . Для того, чтобы интервал вообще не зависел от присутствия
наблюдателя, он не должен зависеть от параметров . Это условие выполняется тогда, когда матрица 
ортогональна при любых значениях её элементов. В таком случае
имеем
, (5.1)
,
(5.2)
где 
- единичная матрица.
Для
квадратной матрицы размерности условие
ортогональности (5.2) представляет собой систему 
нелинейных уравнений,
связывающих её элементы. Однако
вследствие симметрии произведения 
всего 
уравнений взаимно
независимы.
Рассмотрим общий принцип расчёта параметров внутренних наблюдателей
абстрактной системы. Пусть известно на каком-то (малом) участке распределение
состояний в цепи событий некоторой системы, наблюдаемой из внешнего по
отношению к ней мира. Предполагается, что одноимённые состояния разных
подсистем в составе системы различимы. Следовательно, в отношении каждого из
состояний каждой подсистемы известно, сколько раз оно повторялось в цепи
событий на рассматриваемом участке. Назначим
- тую подсистему объектом начала отсчёта и
свяжем с ней внутреннего наблюдателя. Пусть
- тая подсистема будет объектом его
наблюдения. Для наблюдателя, первоначально
внедряемого в систему, коэффициенты , определяющие его отношение к объекту
начала отсчёта, можно принять равными
единице. Необходимо также постулировать скорость движения 
объекта наблюдения (
- той подсистемы) в пространстве наблюдателя, связанного с -
тым объектом начала отсчёта. Проще
всего, внедряя наблюдателя в систему,
принять эту скорость равной нулю. Аналогичным образом поступают в
механике, выбирая систему отсчёта,
неподвижную относительно наблюдателя.
Для
того, чтобы найти значения коэффициентов воспользуемся уравнениями (5.2) и (3.3).
Разделив в уравнениях (3.3) правые и левые части на 
, получим систему уравнений
(5.3)
Количество
неизвестных в
этой системе уравнений равно , а количество независимых уравнений
равно 
.
Единственное
решение система уравнений (5.3) может иметь лишь в том случае, когда количество
неизвестных равно количеству уравнений
,
т.е.
при 
. При 
решений, удовлетворяющих системе уравнений,
может не существовать. При 
имеется множество решений, удовлетворяющих
системе уравнений (5.3).
Какое
может быть дано толкование полученному результату? Осуществив декомпозицию
общей системы на подсистемы размерности и внедряя в систему наблюдателя, для
которого движение каждой подсистемы характеризуется -
мерным вектором скорости, мы поставили в соответствие рассматриваемой
подсистеме точку в -
мерном пространстве. То, что внутреннему наблюдателю представляется точкой в
пространстве, для внешнего наблюдателя является цепью событий, в которой
чередуются состояний некоторой абстрактной
подсистемы. Таким образом, в нашей
модели размерность пространства
определяется размерностью подсистемы, которая отображается в сознании
наблюдателя в виде точки. Как следует из
вышеизложенного, лишь в том случае, когда точке в пространстве соответствует
трёхмерная подсистема, наблюдатель может быть определён однозначно и независимо
от метрики пространства-времени. В двумерном пространстве требование
ортогональности матрицы в
общем случае может быть не совместимым с первыми уравнениями в системе (5.3),
связывающими скорость точки с распределением состояний в цепи событий. Это
означает, что метрика пространства-времени при отображении движения в двумерном
пространстве в общем случае не инвариантна к выбору наблюдателя.
В
пространстве, размерность которого больше трёх, наблюдатель не может быть
определён однозначно. Но если подсистемы размерностью больше трёх рассматривать
как тела, характеризующиеся соответствующим количеством степеней свободы, то
всегда имеется возможность осуществить их декомпозицию на подсистемы (точки)
размерности 3, устраняя этим неопределённость наблюдателя.
Декомпозиция
сложной системы на подсистемы меньшей размерности в общем случае субъективна
(примером тому является декомпозиция звёздного неба на созвездия).
Следовательно, можно ожидать, что в
подавляющем большинстве случаев внутренний наблюдатель абстрактной системы
будет отображать реальность в трёхмерном пространстве, так как
лишь в этом случае пространственный образ реальности в его сознании будет
однозначным и не зависящим от его присутствия.
Внедряя
наблюдателя в систему, мы выбрали в качестве объекта начала отсчёта - тую подсистему. Для
перемещения наблюдателя в пространстве необходимо изменить объект начала
отсчёта. Пусть в качестве нового объекта начала отсчёта, относительно которого
мы хотим рассмотреть движение - той подсистемы,
выбрана - тая подсистема, для
которой известно распределение состояний 
на том же участке цепи
событий, на котором измерены величины . Скорость движения - той подсистемы
относительно - того объекта начала
отсчёта определяется выражением
.
Здесь
неизвестными являются коэффициенты 
и скорость 
. Но последняя может быть выражена через известную скорость 
и скорость движения - той подсистемы
относительно - той в направлении - той координатной оси по правилу сложения скоростей,
удовлетворяющему преобразованиям Лоренца.
.
Подставляя
вместо скорости 
её значение согласно (4.12), получим системууравнений
,
где: 
, 
.
Из этой
системы уравнений находим значения
величин и скоростей . Учитывая, что 
, получаем систему уравнений для определения параметров
наблюдателя 
в отношении - того объекта
наблюдения
Продолжая
вычисления согласно описанному выше алгоритму, можно получить значения
скоростей всех подсистем относительно любого объекта начала отсчёта, а также
матрицы коэффициентов, определяющие внутреннего наблюдателя по отношению к
наблюдаемым объектам.
Однако
величины 
, не вполне
соответствуют компонентам
векторов скоростей, которые могут быть измерены внутренним наблюдателем. Эти
величины получены без учёта релятивистских вкладов в значения скоростей,
обусловленных ортогональными по отношению к данной оси движениями наблюдаемых
объектов. Ортогональное по отношению к - той координатной оси движение вдоль оси 
изменяет скорость,
измеренную вдоль - той оси в 
раз. Следовательно, в трёхмерном пространстве компоненты
вектора скорости, измеренные наблюдателем, будут равны
,
,
.
6. Задача о «привязке» сознания наблюдателя к телу в
пространстве
Имеются
задачи, которые без видимых интеллектуальных усилий решаются нашим сознанием,
но стоит лишь попытаться сформулировать их
в явном виде, как возникают непреодолимые трудности. Подобная задача
обнаруживается, когда мы задаём себе вопрос, каким образом наше сознание «знает» с каким телом оно «сцеплено». Суть
проблемы при традиционном подходе заключается в относительности движения и
невозможности определения координат тел
в пространстве без некоторого базиса –
системы точечных частиц, которые наблюдатель считает взаимно неподвижными друг
относительно друга. Пусть, например,
имеется некоторая система, определённая на множестве точек пространства. До
того как будет определён наблюдатель в этой системе и указан его базис,
невозможно даже предположить, как движутся отдельные точки системы друг
относительно друга. Пусть, например, имеется наблюдатель 
, для которого некоторые точечные частицы 
взаимно неподвижны и
образуют неизменную конструкцию (базис) в пространстве. Совершенно очевидно,
что для иного наблюдателя, скажем 
, частицы могут перемещаться
друг относительно друга. Причём характер их относительного движения зависит от
того, какую подсистему точек 
наблюдатель считает своим базисом.
Пусть, например, хочет передать информацию о том,
какие точки пространства образуют его базис. Оказывается, что выполнить это,
оставаясь в рамках традиционного подхода к понятиям пространства и наблюдателя
в нём, невозможно. Для того чтобы мог реплицировать информацию о своём
базисе, он должен предварительно знать
базис , или они оба должны обладать априорным знанием о некоем абсолютном базисе. Но подобное
предположение либо возвращает нас к идее абсолютного пространства, либо к той
мысли, что информация о базисах всех наблюдателей в системе является априорной
для нашего сознания. В обоих случаях мы фактически выносим проблему за скобки.
Для того
чтобы «прочувствовать» сложность задачи, давайте проведём простой мысленный
эксперимент. Представим себе, что перед нами лист бумаги, краёв которого мы не
видим, и на котором отсутствуют какие-либо ориентиры направлений. Пусть на листе нанесено множество точек,
возможно даже разноцветных, но каждый цвет представлен большим количеством
точек и распределён на листе хаотически, не образуя уникальных цветовых
сочетаний. Допустим, рядом с нами находится наш коллега, который видит ту же
картину. Сосредоточив внимание на некотором подмножестве точек, мы назначаем их
своим базисом. А теперь давайте попробуем объяснить нашему коллеге (не указывая
чем-либо на выбранные точки), какой именно базис мы выбрали. Если бы было
известно, каким базисом он пользуется, то решение данной задачи не вызывало бы
никаких затруднений, но в том-то и дело, что изначально наблюдатели не знают
каким базисом каждый из них пользуется. Как же наше сознание получает
информацию о теле, с которым оно сцеплено? Как передаётся информация об общем
базисе множеству наблюдателей, которые, получив её, обретают возможность
унифицировать язык геометрии и координировать свои действия в пространстве?
Конечно, можно исходить из предположения о том, что в мире существуют абсолютно
твёрдые тела, являющиеся естественным базисом для всех мыслимых наблюдателей.
Но такое предположение плохо согласуется с принципом относительности. Не владея ответами на эти вопросы, мы, тем не
менее, уверены в том, что наше сознание «знает» с каким телом оно сцеплено.
А как эта
задача решается наблюдателями абстрактной системы, заданной на линейно
упорядоченном множестве?
Пусть,
например, для некоторого наблюдателя отрезок истории
объекта наблюдения ( - той подсистемы) представлен цепью событий, в которой
одноимённые состояния повторяются раз. Отрезок истории объекта начала отсчёта ( - той подсистемы) представлен цепью событий, в которой
одноимённые состояния повторяются раз (принимает значения 1,2,3).
Наш
наблюдатель может считать, что данный отрезок цепи событий объекта наблюдения
описывает историю неподвижной точки относительно объекта начала отсчёта,
выбранного им. Принимая 
, 
, найдём для матрицу из системы уравнений
(6.1)
Для того
чтобы реплицировать базис наблюдателя другому наблюдателю достаточно переслать
последнему сообщение о двух последовательностях событий, характеризуемых
распределениями состояний и . Получив эти две последовательности, наблюдатель с помощью системы
уравнений
(6.1), вычислит матрицу . Это будет означать, что ему реплицирован базис наблюдателя (точка для , также как и для , будет неподвижна относительно объекта начала отсчёта ). Далее, пользуясь алгоритмом, описанным в предыдущем
разделе, наблюдатель сможет найти скорости
движения других точек точно такими же, какими их определит для себя .
Таким
образом, сознание наблюдателя оказывается «привязанным» к подмножеству точек
пространства, у которых распределение состояний в цепи событий таково, что 
, 
(одной звёздочкой
обозначен объект наблюдения, двумя звёздочками – объект начала отсчёта).
Информация о выбранном базисе может быть передана другим наблюдателям. Один из
возможных способов подобной репликации может быть осуществлён посредством
передачи генетического кода. Последовательность расположения нуклеотидов в ДНК,
хранящей информацию о теле, с которым «сцеплено» сознание наблюдателя, может
кодировать для биологического объекта, унаследовавшего эту ДНК, цепи событий объекта начала отсчёта и неподвижной
относительно него точки. По известному распределению кодов аминокислот в
этих двух последовательностях вычисляется матрица преобразования частот
повторения этих кодов в векторы скоростей точек. Преобразуя распределение состояний
в цепи наблюдаемых событий с помощью этой матрицы, наблюдатель распознаёт неподвижные и
движущиеся объекты относительно реплицированного ему базиса. Возможно, благодаря подобному механизму, биологические объекты с момента рождения
обладают способностью единообразно распознавать характер движения и покоя тел в
пространстве, образуя популяцию одного базиса.
Список литературы
1.
2. Менский М.Б. УФН 175
414 (2005)
3.
Менский М.Б. Вопросы философии (6) 64 (2004)
4.
Цетлин М. Л. Исследования
по теории автоматов и моделированию биологических систем (М.: Наука, 1969)
5. Эйнштейн
А. О специальной и общей теории
относительности ( В сб. Физика и реальность) (М.: Наука, 1963) c. 167 – 235.
6.
Рашевский П.К. Риманова
геометрия и тензорный анализ (М.: Наука,
1967)