Time as phenomenon of the expanding Universe
Preface
This work was stimulated by Kozyrev’s book [1], that I had read in the 1992. Then I started to reflect on Time meaning and Time and Space asymmetric roles during the Universe Expanding. These ideas development allows to the work [2], it can be accessed now (the Russian version only) on the site of the Institute of time nature explorations (grant № 00-07-90211 of the Russian fund of basic research).
I would like to thank the Chairman of the Russian Interdisciplinary Temporology Seminar Dr. A. Levich from Moscow State University for his constant support and friendly interest. Also I would like to thank A.Moskowsky for the 20-year discussion of the physics history and philosophy.
The noted work [2] pretends to radically revise a number of basic physical concepts relative to the Space - Time, Motion and Energy nature. It includes a detail analysis and mathematical calculations. A brief account of the main part of this work is only presented below.
1. Introduction
The nature of time is not yet enough clear for natural science. In the Newton mechanics time was presented as some universal formal parameter. Its value rises steadily at every point of the Universe. Each physical process occurs in space in correspondence with the time currency.
In the Special Relativity (SR) time and space are integrated to the common 4D-continuum. However, in this theory the time component having imaginary factor seems also to be “exotic”. In this concept the increase of time is also implied in each reference frame.
The General Relativity (GR) allowed link the time properties with gravitational fields and the space geometry. The time currency started being associated with a spatial expansion of the Universe.
So, the theoretical physics traditional approach to the process description is based upon the time currency considering as primary (original) one. They are also in the modern physics [3] several attempts to deduce the time concept as secondary one from different fundamental (microscopic) concepts.
However, the third way (inverse to the first one) is possible and presents the base of this paper. A starting point of this way is the following question: “Does any universal process exist which could generate physical time?“
Such fundamental cosmic process exists really and is well known in the modern science. It presents the Universe expansion and was opened at the first third of the 20th Century by the American astrophysicist E. Hubble and others [4]. It means the general increase of distances between all 3D-bodies. The same scattering of 2D-figures happens on the surface of some spherical balloon during air incoming. The centre of this sphere does not belong to the surface, all points of the sphere (the Universe) are equivalent.
Some time before the theoretical physics came to the same results. As is well known, the Einstein’s GR was published in the 1916. After that Friedmann (1922) proposed the concept of the expanding Universe.
For example, in the book [5] a description of the basic cosmic model is given. I will hereinafter call this model “Einstein-Friedman model”, or “EF-model”. In this model the Universe is presented as 3D-hypersurface of a 4D-sphere with increasing radius. Of course, the curvature of the 3D-hypersurface increases with time too.
2. Basic hypothesis relative to time nature
Some simple and pictorial views consist a base of the new concept. I’ll call it briefly “The Spherical Expanding Universe Theory (SEUT)”.
In the SEUT, like the EF-model, the Universe presents in every time the 3D-hypersurface of a 4D-sphere. However, there is one very important difference. In the Einstein’s theory the spatial components of the metric tensor are opposite in sign to the time’s one. For example, we may consider time as imagine quantity, then a spatial coordinate is real one. On the contrary, in the SEUT the 4D-continuum is considered as purely Euclidean, all the four coordinates are real quantities. The usual spherical geometry can be used on a surface of the 4D-sphere.
As it well known, in the GR the Age of the Universe can be calculate using the EF-model or another one. Usually, the radius-age dependence is not a direct proportionality in such GR models. Well, this result may be deduced if to neglect the global pressure of matter that fills the Universe. I tried to show in [2], that an account of the static pressure of matter follows the Universe radius linear dependence on its age (see below).
On the contrary, in the SEUT the time universal currency is manifested. The Universe age is identified with a current Universe radius divided by the velocity of light. Numerous consequences may be deduced from this statement. On the other hand, it allows avoid many other arbitrary postulates in the model.
3. Mechanical motion and maximal velocity in the SEUT
The SEUT states, there is no unlimited set of independent mechanical motions. Only world lines of moving bodies exist. Each of them has some inclination relative to the time line, which presents a normal to the hypersurface of the 4D-sphere. An inclination angle defines the spatial motion velocity. When the sphere radius rises, the intersection point of word line and current hypersurface “moves” with exact correspondance with a modern physics prediction.
Immovable objects (stars) have the zero inclination, their world line are normal to the hypersurface. Hence they “scatter” according to the Hubble law, their mutual velocity is proportional to mutual distance. If a body world line has some inclination relative to normal, the angle is more than zero. But it can’t exceed 90°, therefore maximal mechanical motion velocity appears naturally, it is equal to the velocity of light.
Let us consider three variants of motion (see for fig.1).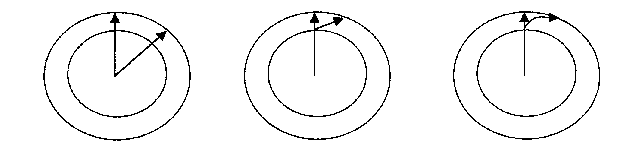
Figure 1. Phenomenon of a “motion” of point on a sphere surface for immovable (at the left), uniformly moving (at the centre) and non-uniformly moving (at the right)
The left picture illustrates the Hubble effect. The right picture presents a general case of motion with acceleration. The central picture corresponds with an inertial motion, its world line is direct. In this case the moving body displacement increases proportionally to the Universe radius increment. So, inertial motion is not postulated in the SEUT, it appears as natural model consequence.
At a large 4-sphere radius values all the relationships of SR and usual mechanics laws are applicable approximately in the SEUT. A Special Relativity light cone transforms to all the hypersurface of the 4D-sphere. But the analogy isn’t complete, because an absolute remote SR area degenerates to this 3D-hypersurface in the SEUT(see for fig. 2).

Figure 2. 4D-continuum areas in the SR (at the left) and in the SEUT (at the right)
4. SEUT and Minkowski geometry
Let us consider small increments of time and space coordinates along body world lines during the Universe expanding. It is enough to consider a small area of the Universe, so we can neglect its curvature. Then it is acceptably to replace approximately concentric hypersurfaces (“isochrones”) by parallel hyperplanes. A rest state corresponds with a representative point “drift” perpendicularly to isochrones, an inertial motion corresponds with displacement along inclined direct lines between isochrones.
At each time the Universe is presented as certain isochrone that contains all the real spatial points. Let us accept that 4D-sphere radius increment divided by velocity of light presents invariant measure of (absolute) time increment. We will also state that this quantity has the same value in each inertial reference frame, i.e. at a motion along each direct world line.
Let the world line inclinations from normal direction are enough small. Then metric relationships like Minkowski geometry ones appears in our purely Euclidean 4D-continuum. In particular, well known relationship
c2 ds2 = c2 dt2 - dr2
can be deduced from the Pythagorean theorem. It connects a spatial component dr with a time component dt (at moving reference frame) through velocity of light c. Here ds is an absolute time interval (between two 4D-events at a immovable reference frame). Hence, if velocities aren’t very high, the Lorentz transform is correct in different inertial reference frames.
5. On the Einstein’s relativity principle
If the world lines inclinations from exact normal direction cannot be accepted as small, then Minkowski geometry relationships are correct approximately only. It means that Einstein’s relativity principle is correct (in the SEUT) only for reference frames that move with velocities enough small relative to selected reference frame. Such reference frame is linked hardly with a body at (absolute) rest, i.e. drifting along radial world line.
The selected reference frame existing reminds of old ether theories that contradict to the Special Relativitiy views. It seems, these theories became a thing of the past irretrievably. In fact, the velocity of light in vacuum is constant everywhere and everywhen. However, the reference frame existing can be detected in principle as a light signal frequency bias, i.e. with the help of Doppler effect. Well, this phenomenon is really detected by modern astrophysics!
The temperature diagram of the Cosmic Microwave Background Radiation (CMBR) coming to the Solar system from all the sides of the Universe is presented on the fig.3. The data was registrated during 4 years by the Cosmic Background Explorer (COBE) satellite (NASA Goddard Flight Center, COBE Science Working Group).
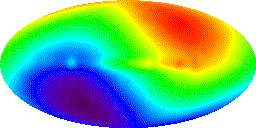
Figure 3. The anisotropy of the Cosmic Microwave Background Radiation (CMBR)
The known Russian scientist J.B. Zeldovitch wrote sooner in the Editorial Addition to [6] that careful measurements allowed find out some anisotropy of CMBR. An antenna oriented to the Lion constellation detects that the radiation temperature is 0.013% more, than mean. The radiation temperature in the opposite direction is 0.013% less, than mean. Generally, a temperature varies continuously between these two values. The isotropy presents only for some imaginary observer. The Solar system, Earth move to the Lion constellation relative to this observer having velocity 390 ± 60 km/s. Hence, as a result of the Doppler effect, a meeting radiation seems to be more hot, and an overtaking radiation seems to be more cold. This example shows that an observer exists in every point of the Universe. For him a CMBR is isotropic. We may consider this observer and the connected reference frame as selected. The selected reference frame existence at the Universe every point looks like the physicists commonly held view preceding to Relativity. They thought that the light presented ether oscillations occupying whole the Universe. They thought also that a reference frame connected with ether was preferable, or selected. They tried to detect the Earth motion relative to ether. We know that these experiments gave the negative result: any ether doesn’t exist. But the Universe evolution follows that when CMBR is observed (and only in this case!), the selected reference frame (called sometime “new ether”) appears. This new ether at one place is moving relative to new ether at other one. The new ether or CMBR just realises the motion according to Hubble’s law.
The modern NASA’s data allows to put the relation of the Solar system velocity to the velocity of light equal to 0,15%. It is enough small value justified Special Relativity and Minkowski geometry relationships application. But can we believe this phenomenon to be an exhaustive proof of the SEUT accuracy?
To test it I propose a not complicated observational experiment. If the CMBR anisotropy is due to the real selected frame existence, then it may be detected for any electromagnetic radiation. In particular, an anisotropy of solar radiation has to exist at the different year periods. It has to be detectable in August, when the both solar radiation and CMBR come to Earth from the Lion costellation side (see for fig. 4). In February these sourses are opposite in disposition relative to Earth, therefore the solar radiation anisotropy direction has to be opposite. The expected effect value (with account of the Lion constellation straight ascendancy and obliquity of the ecliptic) is approximately equal to 300 km/s, i.e. nearly 0,1% of the velocity of light. In November and May the anysotropy has to be practically absent.
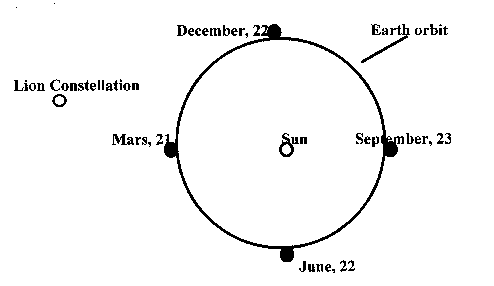
Figure 4. The Sun and Lion constellation disposition relative to Earth
Probably, an analogous SEUT test in a laboratry is realizable with help of artificial radiation sources.
6. Particle mass, energy and impulse
So, we consider the Universe as expanding 3D-hypersurface of a 4D-sphere. Mass localisation places in the Universe present the points of the hypersurface intersection by world lines. So, these world lines have a real physical meaning, not abstract illustrative this one. We may expect this physical meaning to be more essential than simple word expression.
Particularly, while the Universe global analysis is making, we may suppose that such fundamental particle feature as its mass at rest presents some relative value. Such relation (some kind of a quantum number) may include, for example, 4D-sphere (the Universe) diameter and some characteristic size like de Broglie wave period that is inversely proportional to the mass. This hypothesis may make clear inertia nature as two characteristic times relation. It may also explain the energy at rest meaning.
Meanwhile, the Universe radius increases with time. Well, what happens with mass? If a de Broglie wave period increased proportionally to time, we couldn’t generally detect the Universe expansion, including famous “red shift”. But if particle wave periods are constant, then matter mass has to rise proportionally to the Universe age and size.
In the Relativity (like Minkowski geometry) we use vectors having imaginary projection to time axis and real projections to space ones. Particularly, it is true for velocity, acceleration, and energy-impulse 4-vectors. As against, vectors having all the real components are only used in the SEUT. At that, a 4-interval value (length in pseudo-Euclidean space) of some relativistic vector answers the absolute time axis projection of a corresponding SEUT-vector, and imaginary component of a relativistic vector (time of motion) answers the corresponding vector length in purely Euclidean continuum of the SEUT. For example, the energy-impulse vector module presents such quantity. Its projection to absolute time axis is energy at rest divided by velocity of light, and its projections to spatial axis are impulse components. This quantity is constant while the particle movement is inertial one.
A jump to non-inertial motion in the SEUT is connected with a corresponding state vector changement law. So, if particle motion velocity changes, its energy at rest doesn’t change, therefore full acceleration at a time interval can be calculated using the difference between new and old impulse values. Thus, the non-uniform motion equation in the SEUT can be found like SR as time derivative of an impulse expression.
The force-acceleration relation depends on a mutual orientation of force and velocity vectors in the both SR and SEUT. But in Relativity a reference frame velocity can be choised arbitrary, for example – zero, then the relation will be equal to one.
On the contrary, in the SEUT an absolute velocity is presented, it is defined by the world line inclination relative to the normal. Let Earth move vith any velocity relative to the immovable (selected) reference frame. Then we will be able to detect the absolute velocity using two measurements, the first one along the world line, and the second one in a perpendicular direction.
If this absolute velocity is really defined by direction and value following from CMBR anisotropy effect, then we can expect a relative difference near 2,25 х 10-6 between longitudinal acceleration and transversal one.
7. Local gravitational fields of particles
What the SEUT talks about body gravitation fieds? Lte us imagine all the bodies as immovable and drifting exactly along the radial world lines. If there is a mutual attraction effect between two bodies in such Universe, an observer will detect some curvature of their world line. They will seem to be bending one to another instead of a radial divergence. In essence, in this case we may replace a world line by a gravitational field line. Then the analogy allows us to identify an Universe isochronous intersection with an equal potential surface that these field lines have to be normal to. So, we allow to a presentation that a Universe isochronous intersection is not strictly concentric hypersurface. It is perturbed by some kind of craters (see for fig.5), that centres correspondwith gravitating bodies.
Figure 5. A local body gravitation field
The inclination angle of a crater profile relative to non-perturbed sphere hypersurface is equal exactly to the inclination angle of a normal relative to strict radial direction. Hence, a local gravitation field intencity measure agrees practically in each point with body velocity measure that we used earlier. It authorizes energy concept using for both mechanical motion and gravitation phenomenon.
8. SEUT and General Relativity
Let us discuss some GR’s aspects. Is it acceptable to neglect pressure of matter? When Einstein searched for his early cosmological static model solution, he had to introduce a cosmic constant in his equation. This constant answered a negative matter pressure, that Einstein couldn’t determine a meaning. In a non-stationary model a solution exists independently on cosmic constant presence, therefore it may be put often as zero. As rule, bodies velocities may be put as zero too, therefore (dynamic) pressure is usually neglected.
However, I insist on necessity to account a static pressure of gravitating matter. Really, it can be ignored in the case when Einstein’s relativity principle is applicable. Accordingly with it a gravitation field can be always replaced by reference accelerated frame. In this case a purely kinematic side is only accounted. However, not every field may be considered (even locally) as uniform one (see for fig. 6). Let the radius of a field source (or a probe particle) have the same order that the mutual distance. Then the Einstein’s equation connecting space geometry with matter physical features seems to be incomplete. More precisely, it is incorrect to put exactly equal to zero a static pressure in the matter density tensor, it is necessary to introduce its (unknown, calculable) value accounting a continuum deformation energy.
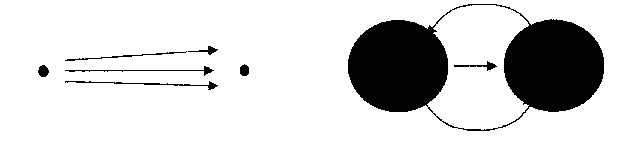
Figure 6. At the left a locally uniform gravitation field is presented, the right field can’t be considered as uniform one even locally
Are the proposed amendments important? Specialists know, that the Metagalaxy gravitation radius is in fact comparable with its real size. In [2] I have showed that the Universe radius is less than its gravitation radius.
Is shown also in the same work [2], that a resulting gravitational pressure in the Universe is negative and answers the Einstein’s cosmic constant. This fact seems to be evident because a gravitation force aims to gripe any matter accumulation. But it is possible to attempt it with help a non-trivial way. Let us consider a matter pressure as a reactive force operating within a uniform sphere of incompressible liquid. A pressure dependence on internal density is presented in [7]. We can see (see for [2]), that if the sphere gravitation radius exceeds its geometric radius not more than approximately 1% (or is still less), then a pressure sudden negative change appears at the internal abroad. This phenomenon may be explained as a volume “expansion” due to a metrics perturbation.
The static pressure account allows not only to find out a new (linear in time) cosmologic solution, but also to calculate a Universe gravitational pressure value in dependence on its radius. This negative value has the representation like that one for a non-relativistic sphere (a star or a planet, for example). Also I would like to note, the expression for density-Universe radius in the SEUT is exactly the same that the expression for so-called critical density in the EF-model.
Two very important circumstances are clarified for all that. First, the Universe mass was turned out as linearly increasing function of the 4D-sphere radius, not constant. A famous Einstein’s programme is realized unexpectedly in the SEUT: a matter features (density) are reduced to a space features (curvature). In other words, a necessity to externally (“by hands”) introduce a mass distribution in the equations is eliminated in the SEUT. This operation is need in the GR to find out a spatial metrics changement law.
Second, the seeming paradoxicality of University mass (and energy!) non-conservation forces to reflect on conditions that the accomplishment allows to the energy conservation law correctness (see for fig.7).
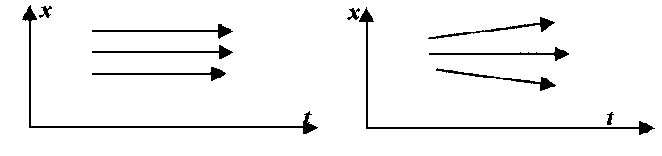
Figure 7. If space features aren’t depending on time, then the closed system energy is constant (at the left). But if space features evolve in time, then the closed system energy haven’t to be constant.
It is evident, I believe, the energy can be exactly constant only in such physical system (or in whole the Universe) for which space features (in particular, a curvature) are strictly constant in time too. However, the both modern physics and SEUT issue from the opposite concept. Hence, this state can only be accomplished approximately, moderately of a bit of the modern rate of a relative space curvature evolution. This rate has order 10-10 per year for the modern Universe.
N.A.Kozyrev [1] basing on astrophysical observations stated the common star radiation origin that has to be due to the time-energy transformation. Accordinly with the SEUT, the star mass and energy at rest realative increment is equal to the Universe age relative increment. It is interest, Sun mass relative lost due to the radiation consists in 10-15 per year, i.e. five orders less.
9. Universe origin and closed geometry
The cosmological EF-model couldn’t say anything on the Universe origin. On the contrary, the work [2] approach allows an obvious way to study the problem.
As it is noted in [7], the metrics of any sphere area having a non-zero density is perturbed relative to Euclidean one, its geometry agrees with 4D-sphere hypersurface geometry. For non-collapsing sphere its gravitation potential relief is like a very small “pit” that gravitation radius is much less than its geometric size. However, when the density rises, the metrics perturbs more and more, and the pit transforms to some kind of “crater”. The crater is connected with the external surface by a narrow neck. Only this neck or its part is visible for an external observer, and the gravitation insurmountable barrier transmutes an object central area into “a lost world”.
From the point of view of the external world, the central area presents a “black whole” absorbing irreversibly all the matter and radiation. On the other hand, for our Universe inhabitant the “navel-string” connecting with the external world has to seem a spherical “white whole”, to which a matter and radiation are coming continuously (and, may be, carry out an information on the external world features). There is an old Russian fiction science book called “Sannikov Land”, where an internal gigantic trench concerning central small star is described. Our model seems to be like this picture.
Is it possible, we live in such black whole? My hypothesis answers affirmatively this question. The negative sign of the matter pressure due to continuously increasing our world size allows to such conclusion. And the University restraint can be physically explained by the way.
On the other hand, as I showed in [2], in spite of matter average density negligibly small, the Universe gravitation radius is more than its geometrical radius, hence, it presents a black whole. This condition accomplishment agrees the Universe restraint, the boundary absence in spite of its finite volume. Also, this fact confirms our assumption that the Universe energy at rest localisation area doesn’t exceed the gravity operation area.
A specific model of star collapse is created in the modern General Relativity. In general, it can study in three different reference frames. As a rule, the “point mass” models are used. First model is linked with an external observer, second one accompanies a matter falling to the black whole. Third model presents an internal reference frame, i.e. an observer within collapsing object.
From point of view an external observer the matter falling time to the black whole is infinitely large. However, in an accompanying reference frame it is finite. Since in the accompanying reference frame time and space coordinates are expressed through the both types of external reference frame coordinates. What is more, in the internal reference frame the time and space coordinates quite trade places, the metrics tensor components are depending on time. Further, any matter point history in this accompanying reference frame starts at the zero moment and finishes after same universal time period in a special (singular) point, after which nothing exists (“time barrier”).
As I believe, another lacing between internal and external collapse picures is possible, if we will consider a non-point collapsing object. Nobody wonders now at a situation, when a time period can be finite in one reference frame and infinite in another one. Therefore, we can believe, unlimited black whole collapse in the external Super-Universe may seem to present unlimited expansion of our Universe observing inside. This expansion seems to start from a singular point, and the same point is the history end of all the matter of the external Super-Universe that fall to the black whole. I would like to note especially, it doesn’t mean that internal time pass in opposite to external one. Faster, it is possible to state, time within a black whole pass ortogonally to external one.
1. N.A.Kozyrev. Selected works. Leningrad, Leningrad State University Publishing, 1991 (in Russian).
2. U.S.Vladimirov. The Space-Time and Interaction Realational Theory. Part 2. The Physical Interaction Theory. Moscow State University Publishing, 1998 (in Russian).
3. A.S.Sharov, I.D.Novikoff. A man who discovered the Universe Bang. The Edvin Hubble Life and Labour. Moscow, Nauka, 1989 (in Russian).
4. A.Einstein. TheMeaning of Relativity. Princeton, 1953.
5. S.Weinberg. The first three minutes. A modern View of the Origin of the Universe. Basic Books, Inc. Publishers, New York, 1977.
6. R.C.Tolman. Relativity, Thermodynamics and Cosmology. Oxford, Clarendon Press, 1934.


